AR模型的功率譜估計方法及在故障檢測中的應用
姚志飛,姜萬錄,朱勇
(1.河北廣播電視大學,河北石家莊050090;2.燕山大學,河北秦皇島066004)
干式真空泵目前主要應用于航天及航天衛星器件的地面性能測試系統、科學研究機構及高等院校實驗室的真空獲得設備、化學工業、生物及化學制藥、光學器件過程工藝、半導體器件工藝制造、液晶生產、蝕刻和鍍膜等行業中。隨著真空應用領域的不斷發展和真空應用要求的提高,傳統的油潤滑真空設備已經越來越不能夠滿足市場的苛刻要求。因此,出現了各種不同類型的干式真空泵,以滿足市場上需要的無油潔凈真空的要求。隨之而來的對干式真空泵的故障檢測也成為亟需解決的問題。
目前,在滾動軸承的故障診斷中,通常采用將振動信號進行基于Fourier 變換的經典譜分析方法,并從中提取故障特征信息,再進一步判斷軸承的工作狀態。但經典譜估計存在缺陷:(1)弱信號被強信號的旁瓣所淹沒;(2)頻率分辨率約為數據長度的倒數,導致分辨率不高;(3)頻譜存有旁瓣,導致出現“泄漏”現象而使主瓣失真。雖然,之后出現了幾種改進算法改善了譜估計的性能,但仍未能有效地克服上述缺點[1]。
現代譜分析方法利用被窗函數截取的有限信號以外的信息進行預測或外推,從而避免了功率泄漏,提高了分辨率。其中,參數模型法是較為常用、有效的方法,而有理參數模型中最成熟和常用的是AR模型[2]。作者將其應用于干式真空泵的滾動軸承故障檢測,以設有內圈故障缺陷的滾動軸承振動信號為例進行驗證,取得了較好的診斷結果。
1 AR模型及AR 功率譜
AR模型即自回歸模型,該模型的當前輸出是當前輸入和過去輸出的加權和,可用如下差分方程來表示:
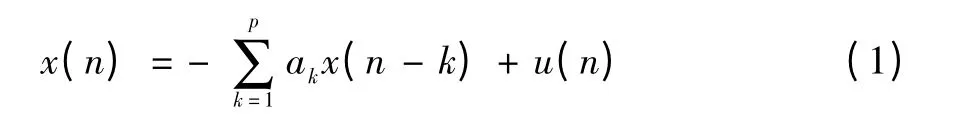
其中:ak(k=1,2,…,p)為AR模型的參數;p為AR模型階數;u(n)為均值為零、方差為σ2的平穩白噪聲序列。
由上式所定義的AR(p)過程{x(n)}可以看作是白噪聲序列u(n)通過一個傳遞函數為

的全極點濾波器所產生,因此{x(n)}的功率譜密度px(ejω)可表示為:

從上式可以看出,只要求得參數ak(k=1,2,…,p)和σ2即可估計出{x(n)}的功率譜密度。
2 AR模型參數估計及最佳階次選擇
建模的關鍵是把模型的階數和參數全部估計出來。AR參數估計的常用方法有:Yule-Walker或自相關法、最小二乘法、Burg算法等。作者采用計算簡單、處理速度快、精度高的Yule-Walker方法,然后用Levinson-Durbin 遞歸算法計算AR模型系數[3]。
Yule-Walker方法主要基于一組被稱為Yule-Walker方程的線性方程,它是聯系自相關序列和AR模型參數的方程。可以通過計算含p+1階自相關系數的Yule-Walker方程,計算p+1階模型參數。

對于真實信號,由自相關函數的偶對稱性可知Rx(m)=Rx(-m)。上式可寫成矩陣形式:

在AR 譜估計中,模型階次的選擇是一個關鍵問題。階次太低將會導致過于平滑的譜估計結果,頻率分辨率過低;而階次太高,將會產生虛假譜峰,并且估計的方差也會增大。文中采用最終預測誤差準則(FPE)判斷最優階次。該準則的計算公式為:
其中:N為數據點數;p為待估計參數,對AR(n)模型,p=n;為模型殘差。
a 開始隨著p的增大而減小,但當p 超過序列的真正模型階數p0之后,值不再減少,這時將起著主導作用。因此,使FPE(p)取最小值的那個p 就可以判定為模型的最佳階次,即

其中:L為預先設定的模型階次上界。在階次上界范圍內,FPE 會存在若干個極小值,其中最小值對應的階次為FPE 判階準則給出的最佳階次。顯然,這樣確定的最佳階次與定階上界有關,如果定階上界選得過小,所得最合適階次將會偏低;如果定階上界選得過大,將加大計算量。因此,階次上界的確定非常重要。目前人們只給出了樣本長度N 在20~200之間的AR模型階次確定的經驗準則(即定階上界)[4],但這并不適用于滾動軸承振動信號。文獻[5]指出,估計階次的上界L與樣本長度N之間的關系為:但文中既沒有給出理論推導,也沒有給出實際驗證。文獻[6]通過實驗研究表明,將樣本長度的均方根值作為滾動軸承AR模型的定階上界,可以得出滿意的AR模型分析結果。
參數估計是在給定階次的情況下進行的。由于事先無法判斷模型的階次,因此在建模過程中先給定模型的階次,然后按照Yule-Walker法估計出AR模型的參數,得到相應階次模型,最后取FPE(p)值最小的階次作為模型的最佳階次,同時也確定了AR模型。
3 AR模型分析在干式真空泵故障檢測中的應用
滾動軸承常見的故障形式有內、外圈滾動面及滾動體表面的劃痕、剝落、磕傷,以及保持架的斷裂等。文中以干式真空泵滾動軸承內圈故障的振動信號為例進行AR 建模,并估計了其AR 譜,進行故障分析。在軸承外圈固定的情況下,滾動軸承內圈故障特征頻率[7]:

其中:fr為內圈的旋轉頻率,D為軸承節徑,d為滾動體直徑,α為接觸角,z為滾動體個數。已知試驗中fr=105 Hz,D=46.2 mm,d=9.525 mm,z=9,α=24.97°,代入式(9)可求得fi=550 Hz。
實驗采用的干式真空泵為5級羅茨+爪型干式真空泵,泵體結構示意圖如圖1所示。泵的每個轉子都由固定于高、低真空端的一對單列深溝陶瓷軸承來固定。泵入口壓力為2 kPa,軸轉動頻率為105 Hz。振動傳感器ADXL105 (ADXL-HV)和BK4370V (BKHV)被安裝在干式真空泵高真空端,另一只振動傳感器ADXL105 (ADXL-LV)被安裝在干式真空泵低真空端。振動信號由采樣頻率為40 Hz的數據采集卡采集,通過A/D轉換器得到數字信號。振動加速度傳感器的采樣點數為80 000[8]。

圖1 干式真空泵結構示意圖
實驗中,采用3種測試工況:正常運行的泵1 和泵2,引入軸承故障的泵1。
在一定的氣體負載范圍內 (入口壓力0~100 kPa),選用加速度傳感器ADXL-HV 采集正常泵1 高真空端的無故障振動信號,得到基于AR模型的功率譜圖,如圖2所示。可以看出,無故障振動信號的典型的頻譜含有諧波振動信號及其倍頻的譜峰。采集真空泵有故障時振動信號,得到基于AR模型的功率譜,如圖3所示。當在一個軸承上引入故障以后,其頻譜就會有顯著的差別,出現了頻率為550 Hz的頻峰。

圖2 不同入口壓力時無故障振動信號的功率譜圖
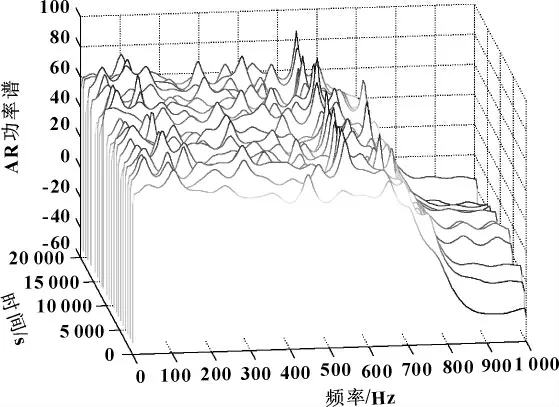
圖3 不同入口壓力時故障振動信號的功率譜圖
為了對比有無故障的頻譜圖,作者將以上兩個三維圖疊加形成二維圖,如圖4所示。可知:故障特征頻率大約為550 Hz,可初步判定為軸承內環故障。

圖4 ADXL-HV 捕獲的有故障與無故障功率譜的對比圖
同理,采用加速度傳感器ADXL-LV 采集3種工況的低真空端振動信號分析得到功率譜圖,疊加后的二維譜圖如圖5所示。用加速度傳感器BK-HV 采集3種工況的高真空端的振動信號并作出其功率譜圖,疊加后的二維譜圖如圖6所示。
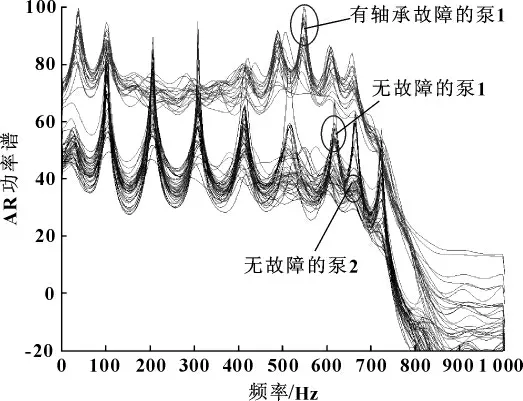
圖5 ADXL-LV 捕獲的有故障與無故障功率譜的對比圖

圖6 BK-HV 捕獲的有故障與無故障功率譜的對比圖
對比3種工況振動信號的基于AR模型的功率譜,其故障特征頻率都明顯出現在550 Hz處。因此,可以進一步判斷故障形式為軸承內環故障,這同試驗所設定的故障形式吻合。
4 結論
對干式真空泵的滾動軸承故障進行了研究,分析了AR模型最佳參數選擇原則,并運用AR 功率譜分析方法對泵實驗數據進行了分析。實驗研究結果表明:基于AR模型的功率譜分析方法對于干式真空泵的故障檢測是有效的,為干式真空泵故障診斷的研究提供了一種可靠的方法。
【1】陸傳賚.現代信號處理導論[M].北京:北京郵電大學出版社,2002.
【2】胡廣書.數字信號處理[M].北京:清華大學出版社,2002.
【3】姚志飛.AR模型最佳階次選擇及其在故障檢測中的應用研究[D].秦皇島:燕山大學,2008.
【4】楊叔子,吳雅.時間序列分析的工程應用[M].武漢:華中理工大學出版社,1994.
【5】沈鳳麟,葉中付,錢玉美.信號統計分析與處理[M].合肥:中國科學技術大學出版社,2002.
【6】趙聯春,馬家駒,范樹遷,等.滾動軸承振動分析中的AR模型研究[J].中國機械工程,2004(3):210-213.
【7】張晨罡,郝偉.基于AR模型的滾動軸承故障檢測[J].現代制造技術與設備,2006(5):35-40.
【8】JIANG W,SPURGEON S K,TWIDDLE J A,et al.A Wavelet Cluster-based Band-pass Filtering and Envelope Demodulation Approach with Application to Fault Diagnosis in a Dry Vacuum Pump[C]//Proceedings of the Institution of Mechanical Engineers:Part C,2007:1279-1286.

