銑削加工曲面殘余應力有限元分析

曾紅，韓笑，陳燕燕，王延忠，吳林峰

(1.遼寧工業(yè)大學機械工程及自動化學院，遼寧錦州121001;2.北京航空航天大學機械制造及自動化學院，北京100191)

殘余應力是消除外力或不均勻溫度場等的作用仍留在物體內(nèi)的自相平衡內(nèi)應力。殘余應力對于構件的疲勞強度、應力腐蝕、形狀精度等均有重大的影響，而它的形成又隨構件的材質、形狀、成形與加工工藝過程等的不同而異。如何評定殘余應力的大小、調整殘余應力的分布、減小或消除殘余應力對工程的影響已成為人們廣泛關注的問題[1]。因此，分析加工過程中加工參數(shù)對殘余應力的影響，對于優(yōu)化切削過程和防止加工零件過早疲勞破壞，是很有必要的。

目前的仿真分析多為采用有限元仿真方法對平面進行的二維切削仿真和簡單的平面三維仿真，通過對切削過程的模擬，研究切削用量、刀具參數(shù)對已加工表面殘余應力的影響規(guī)律。而目前尚無針對曲面的銑削加工過程的低應力加工仿真，因此有必要開展曲面的低應力切削控制研究。

1 殘余應力的產(chǎn)生機理

已加工表面殘余應力產(chǎn)生的原因，可以概括為機械應力和熱應力引起的塑性變形效應[2]。

(1)機械應力塑性變形效應

如圖1所示，在剪切區(qū)，金屬切削層在切削速度方向上承受壓應力，使已加工表面在該方向產(chǎn)生殘余拉應力。在刀/工區(qū)，切削層金屬沿著刀刃鈍圓面流動時受到刀具的擠壓而產(chǎn)生塑性流動，使表層發(fā)生了延展現(xiàn)象。而里層金屬發(fā)生彈性變形，對表層的延展起到牽制作用。之后，切削層金屬受到后刀面強烈的摩擦作用，使表層發(fā)生大塑性變形，而里層金屬發(fā)生彈性變形。切削過后，刀具的作用力消失，里層金屬的彈性變形趨向恢復，但受到表層金屬的牽制，因而在里層產(chǎn)生拉應力、表層產(chǎn)生壓應力。

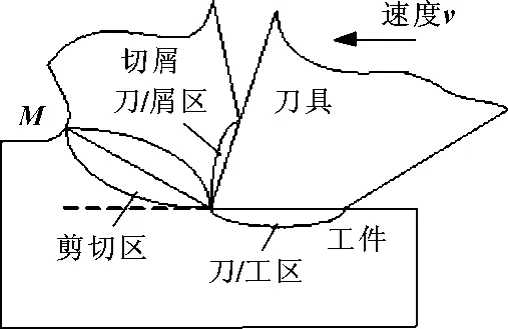
圖1 切削變形區(qū)

(2)熱應力塑性變形效應

在剪切區(qū)，由于強烈的塑性變形，產(chǎn)生變形熱;在刀/工區(qū)，金屬受到鈍圓面和后刀面的擠壓、摩擦，產(chǎn)生塑性變形熱和摩擦熱。這些熱使得工件表層的溫度比里層的高，表層的膨脹速度比里層大，但同時又受到里層的阻礙，使表層產(chǎn)生壓應力。當切削過后，表層和里層的溫度都下降到室溫，表層收縮多，里層收縮少，表層的收縮受里層的牽制，因而使表層產(chǎn)生拉應力、里層產(chǎn)生壓應力。

在切削過程中，引起不均勻塑性變形的機械應力和熱應力是同時存在的，所以殘余應力的計算是一個熱－力耦合熱彈塑性問題。

2 有限元模型的建立

進行曲面的銑削加工仿真過程時，材料的設定基于如下假設進行:

(1)工件材料為理想熱－彈塑性體，均勻連續(xù)、各向同性、不可壓縮;屈服極限服從Mises 準則，切屑的塑性流動過程連續(xù)且穩(wěn)定。

(2)刀具和工件、切屑之間的摩擦因數(shù)恒定，不隨溫度、材料物理性能變化而變化。

(3)刀具為剛體，不隨切削過程發(fā)生變形。

由于塑性變形和傳熱發(fā)生在同一空間域和時間域，而二者又分屬不同的物理問題，分析時基于不同的基本理論[3]。為此，要采用熱－力耦合的有限元算法。為在仿真過程中模擬以上熱、應力－應變耦合的工件變形和應力應變狀態(tài)，需要能描述材料在大應變、寬應變率范圍以及寬溫度范圍內(nèi)力學行為的本構模型。文中采用的Johnson-Cook模型是描述金屬材料相關動態(tài)響應的本構模型，適用于描述金屬材料從低應變率到高應變率下的動態(tài)行為，考慮了溫度、應變率和應變等因素。

文中的擬加工橢球面兩個方向的主曲率分別為K1=0.005 77，K2=0.013 82，即橢球面的長短軸分別為R1=173 mm，R2=72 mm。工件材料為常用的45號鋼，該材料的Johnson-Cook參數(shù)[4]如表1，失效參數(shù)如表2。刀具采用的為φ8 mm的球頭銑刀。其中，圖2為Abaqus 中的分析模型。切削過程中工件外側定義為全約束，刀具繞刀軸旋轉的同時，刀尖沿著工件表面做曲線運動。

表1 Johnson-Cook參數(shù)

表2 失效參數(shù)

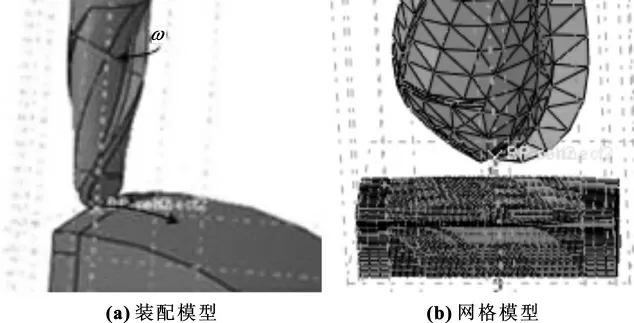
圖2 Abaqus 中的模型

3 表面殘余應力的結果分析

文中采用主軸轉速分別為3 000、5 000、8 000 r/min，單齒進給量分別為0.05、0.1、0.2 mm/齒，切削深度分別為1、2、3 mm 作為曲面銑削加工的參數(shù)，對加工過程進行了仿真分析，得到了殘余應力在不同的參數(shù)條件下的變化曲線，見圖3。

圖3 表面殘余應力變化曲線

圖3為單齒進給量、切削深度、主軸轉速不同的情況下，表面殘余應力的變化曲線。可以看出:距離表面一定深度區(qū)域的殘余應力大部分位于0 線以下，是表面的殘余壓應力，壓應力呈先增大后減小的變化趨勢。其中，圖3(a)是在主軸轉速為3 000 r/min、切削深度為1 mm時，不同的單齒進給量下殘余應力的曲線圖。可以看出:隨著單齒進給量的增大，表面殘余拉應力增大，出現(xiàn)最大殘余壓應力的深度由0.35 mm 增大到0.8 mm，由壓應力轉換為拉應力的深度即塑性變形深度由0.58 mm 增大到1.25 mm;圖3(b)是主軸轉速為3 000 r/min、單齒進給量為0.05 mm/齒時，在不同的切削深度下殘余應力的曲線圖。可以看出:隨著切削深度的增大，工件殘余壓應力的深度也隨之增大，工件發(fā)生塑性變形的深度加深。產(chǎn)生殘余壓應力增大這一現(xiàn)象的原因是:由于切削深度增大，增大了切削過程中的切削力，刀具對工件的作用力增大，導致工件殘余壓應力的范圍加深。

圖3(c)是單齒進給量為0.05 mm/齒，切削深度為1 mm時，不同的主軸轉速下殘余應力的曲線圖。可以看出:隨著刀軸轉速的提高，表面殘余壓應力有所減小，拉應力增大;同時，塑性變形深度也隨之增大。產(chǎn)生這一現(xiàn)象的原因是:在相同的進給速度下，主軸轉速增大了，增大了刀具與工件之間的摩擦熱量，使工件表面的殘余拉應力增大，壓應力減小。

4 基于有限元的正交試驗

通過以上曲線圖的分析，只能得到在某一參數(shù)變量條件下，殘余應力的變化趨勢，不能比較不同的切削參數(shù)對殘余應力的影響程度。為了得出主軸轉速、單齒進給量及切削深度等切削參數(shù)對殘余應力影響程度，基于有限元分析模型，設計了一組四因素三水平的正交試驗。表3所示為L9(34)四因素三水平正交試驗的因素及水平值。文中只選擇了3個元素，即主軸轉速、切削速度(銑削模擬中為單齒切削量)、切削深度[5]。

表3 因素及水平值

表4為曲面切削加工模擬結果正交表。利用有限元軟件進行了9次切削仿真，得到己加工表面殘余應力的結果，包括切削速度方向的殘余壓應力平均值、最大壓應力值及塑性變形深度。

表4 切削模擬結果正交表

從表4的極差值R分析中，可以看出:主軸轉速取3 000 r/min時，表面的殘余壓應力最大，塑性變形深度最小;單齒進給量為0.2 mm/齒時，表面壓應力最大，塑性變形深度最大;切削深度為3 mm時，表面殘余壓應力比其他兩水平大，塑性變形深度也大。同時還可以看出:三因素中，單齒進給量對工件塑性變形深度影響最大，切削深度次之;切削深度對表面殘余壓應力的影響最大，單齒進給量次之;主軸轉速對兩者的影響都最小。在實際加工過程中，由于切削深度的增大會導致加工精度的降低，因此，為增大表面殘余壓應力與壓應力在深度上的分布范圍，應在滿足加工精度要求的切削深度前提下，盡量增大加工過程中的單齒進給量。

5 結束語

通過對曲面銑削加工過程的三維仿真，研究了曲面銑削加工過程中殘余應力的產(chǎn)生機制和影響因素，利用三維有限元仿真驗證了切削過程中工件、切削應力變形的切削理論;并通過針對不同主軸轉速、單齒進給量和切削深度組合的仿真實例，得到了切削表面的殘余應力在進給方向上沿深度的分布，得到了不同主軸轉速、單齒進給量和切削深度的殘余應力變化曲線，并進行了分析。

仍有需要進一步探討的地方，如:

(1)計算過程中刀具和工件、切屑之間的摩擦因數(shù)是隨溫度等變化而變化的，在文中的分析中沒有涉及，需要進一步研究。

(2)實際加工過程中，刀具并非完全的剛體，存在一定的損耗，而文中在計算過程中，將刀具假定為剛體，未考慮刀具的磨損情況，需作進一步的研究。

(3)目前的仿真參數(shù)僅考慮了加工參數(shù)，并未考慮工件及刀具的材料及刀具的幾何外形，后續(xù)還可進一步對更多的參數(shù)進行仿真分析。

【1】劉建明，朱小清.汽車滲碳淬火齒輪的表面殘余應力研究[J].熱處理，2006(2):50－51.

【2】蔡在宣.金屬切削原理[M].上海:同濟大學出版社，1994.

【3】張鐵茂.金屬切削學[M].北京:兵器工業(yè)出版社，1991.

【4】陳剛，陳忠富，徐偉芳，等.45 鋼的J-C 損傷失效參量研究[J].爆炸與沖擊，2007，27(2)，131－135.

【5】袁哲俊.金屬切削實驗技術[M].北京:機械工業(yè)出版社，1988.

【6】郭培燕.高速切削加工表面殘余應力的分析和模擬[D].青島:山東科技大學，2007:17－22，42－48.

【7】JOHNSON K L.Contact Mechanics[M].Cambridge University Press，1985.

【8】周軍.鋁合金7050－T7451 直角切削表面的殘余應力研究[J].工具技術，2010，44(2):12－16.

【9】何慶稀.鋁合金7475 已加工表面殘余應力的數(shù)值模擬[J].制造，2008，46(6):46－49.