基于NSCT的紅外與可見光圖像融合方法

張驚雷，趙俄英

(1．天津市復雜控制理論及應用重點實驗室，天津300384;2．天津理工大學自動化學院，天津300384)

1 引言

隨著電子信息技術和多傳感器技術的快速發展，圖像融合技術被廣泛應用于遙感、軍事、醫學圖像處理、目標識別、人臉識別和計算機視覺等領域［1］。圖像融合就是通過特定的算法對由不同傳感器所得到的同一場景的圖像進行處理，以得到對場景內容更為可靠、清晰和準確描述的圖像。圖像融合通常可分為像素級融合、特征級融合和決策級融合［2］。在圖像處理領域，像素級圖像融合是其他融合方法的基礎，基于多尺度分解的多分辨率圖像融合是圖像處理的一個重要分支。近年來，在多分辨率圖像融合領域取得了許多研究成果。大部分的方法都是基于金字塔變換。其中，小波變換成為圖像融合領域的研究熱點，因為它具有多分辨率特性和良好的時－頻特性，但小波在每一個分解層僅能捕捉有限的方向信息(包括水平方向、垂直方向和對角方向)。為此，學者們經過不斷實驗提出了新的圖像表示方法，如脊波變換、曲波變換，但效果仍不理想。2002年，Minh N．Do和Martin Vetterli提出的Contourlet變換［3］是一種有效的二維圖像表示方法，有很好的方向性和多分辨率特性。在輪廓波變換中，多尺度分解和多方向分解是彼此獨立的。首先用拉普拉斯金字塔變換對圖像進行多尺度分解，然后再用方向濾波器組濾除由每一個拉普拉斯金字塔通道所得圖像的高頻分量。用基于輪廓波變換的融合方法所得到的融合圖像比前面幾種融合方法要好。但由于在拉普拉斯金字塔分解與方向濾波器組中下采樣與上采樣的存在，使得輪廓波變換缺乏平移不變性，從而導致了Pseudo-Gibbs效應［4］的產生，這對于融合處理來說是不利的。于2006年由A．L．Cunha等提出的 NSCT(non-subsampled contourlet transform)［5］，不僅繼承了 Contourlet變換所有的多尺度、多方向特性，還具有平移不變性。它是輪廓波變換平移不變的一個版本。本文在分析NSCT的基礎上，針對紅外與可見光圖像在融合時亮點目標易丟失且背景的邊緣、紋理信息不夠清晰的問題，提出基于非下采樣輪廓波變換(NSCT)與局部區域融合規則相結合的紅外與可見光圖像融合方法。

2 NSCT的基本原理

NSCT是通過采用非下采樣金字塔分解和非下采樣方向濾波器組來實現圖像的多尺度、多方向分解。NSCT是一種新的圖像幾何表示方法，與輪廓波變換相比，NSCT是平移不變的并且比Contourlet變換能更好地采集頻率且具規律性，由NSCT分解得到的多尺度、多方向圖像與原始圖像尺寸相同。

2．1 非下采樣金字塔(NSP)

非下采樣金字塔框架是一個雙通道非下采樣濾波器組，主要是通過二通道非下采樣濾波器組來實現的。理想的非下采樣金字塔濾波器組的頻率響應如圖1所示。非下采樣濾波器組由于沒有下采樣和上采樣，所以具有平移不變的特性。

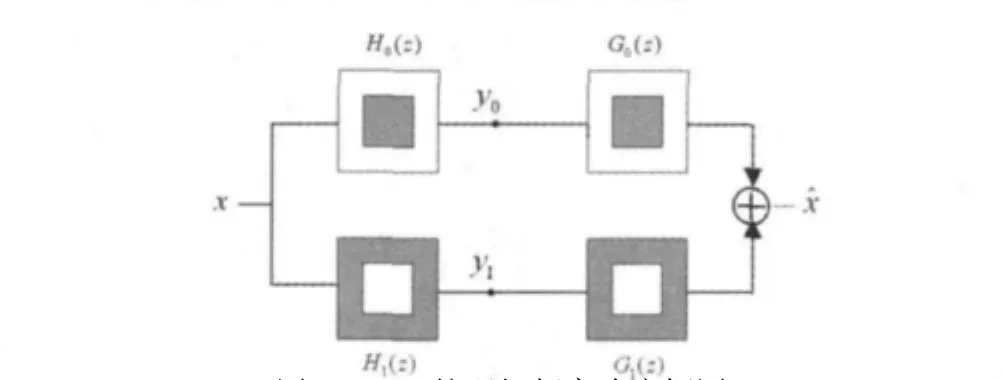
圖1 NSP的理想頻率響應框圖

對于雙通道濾波器組來說，要實現分解后的完全重構，濾波器必須滿足等式(1):

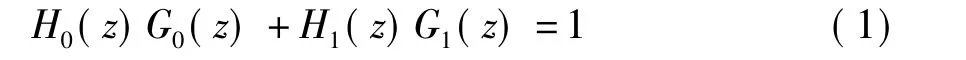
其中，H0(z)和H1(z)表示雙通道分解濾波器的頻率響應;G0(z)和G1(z)表示雙通道合成濾波器的頻率響應。為了實現圖像的多尺度分解，可以通過迭代非下采樣濾波器組來構建NSP。

2．2 非下采樣方向濾波器組(NSDFB)

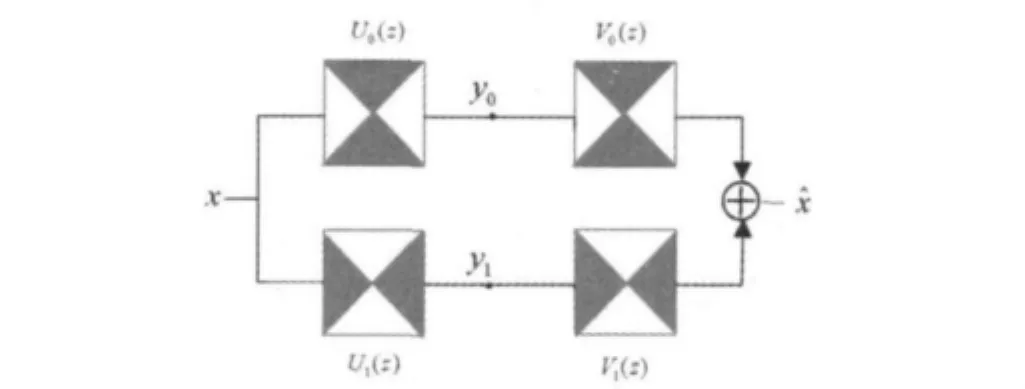
圖2 NSDFB的理想頻率響應框圖

非下采樣方向濾波器組也是一個雙通道非下采樣濾波器組，實際上是Contourlet中的方向濾波器組(DFB)具有了平移不變性，非下采樣方向濾波器組的理想頻率響應如圖2所示。其中，U0，U1為分解扇形濾波器;V0，V1為重構扇形濾波器，并且容易驗證它們滿足完全重構的條件，即U0(ω)V0(ω)+U1(ω)V1(ω)=1。對得到的頻域中的扇形濾波器作z變換就可得到z變換域中的分解扇形濾波器組U0(z)，U1(z)和重構扇形濾波器組V0(z)，V1(z)。為得到更為精細的方向分解，可以通過迭代非下采樣濾波器組來構建NSDFB。

2．3 NSCT 的實現

NSCT是由 NSP和 NSDFB構成的，如圖3所示。NSP提供多尺度分解，NSDFB提供方向性分解。這一過程可以在由NSP輸出的低通子帶上重復迭代而實現。

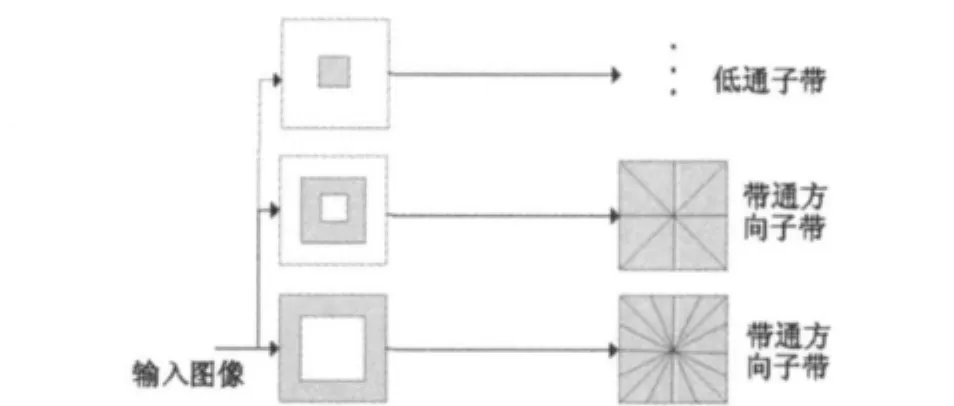
圖3 NSCT的多尺度分解框架

組合的結果是一個雙重迭代濾波器組結構，叫做非下采樣輪廓波濾波器組，它能把圖像在多尺度上分解成方向子帶。

3 基于NSCT的圖像融合方法

3．1 融合方法

待融合的兩幅圖像需是幾何上彼此經過配準的，對于每一幅圖像來說背景信息屬于低頻部分，邊緣和紋理信息則屬于高頻部分。因此，我們首先運用NSCT對圖像進行多尺度、多方向分解，把每一幅圖像分解成低頻低通子帶部分和高頻帶通子帶部分，然后針對各部分運用不同的融合規則進行融合。最后，通過逆NSCT對融合系數進行重構得到融合圖像。基于NSCT與局部區域融合規則相結合的紅外與可見光圖像融合框圖如圖4所示。

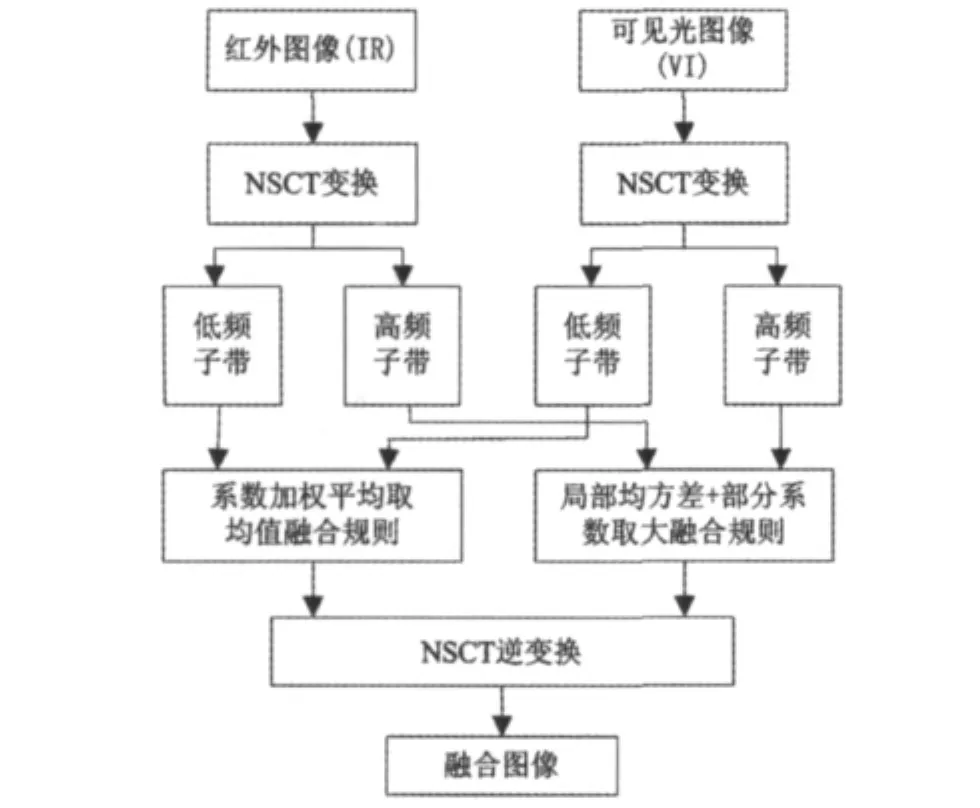
圖4 基于NSCT的紅外與可見光圖像融合框圖

3．2 融合規則

針對不同部分運用不同融合規則融合由分解得到的多尺度和多方向圖像系數。低頻部分包括了大部分的背景信息，融合規則采用低頻系數加權平均求均值的選擇方法。首先對兩幅圖像的低頻分量進行加權，本文選擇3×3的窗口模塊對低頻系數進行加權，然后再對加權平均后的系數求均值得到低頻融合系數。其具體計算公式如式(2)所示:

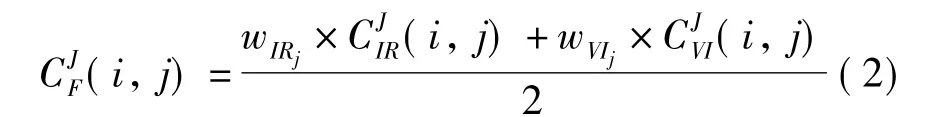
高頻部分包含了大部分的圖像細節(邊緣和紋理信息)。如果采用系數值選大法則容易失去圖像的細節及紋理部分，如選用區域融合規則可能影響圖像的清晰度及對比度。根據這一情況采用系數值選大法與局部區域融合規則相結合的融合方法。

對于方向數少的高頻子帶(文中取≤4的方向)采用系數值選大法，即對兩幅圖像同一位置的高頻系數進行比較取較大的那個作為融合系數，計算方法如式(3)所示:

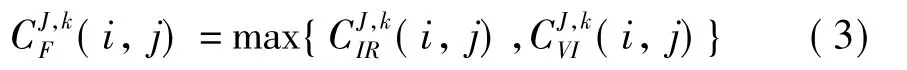
在方向數多的高頻子帶(文中取＞4的方向)選擇以系數為中心的基于局部區域均方差的融合規則。具體過程可分三步:

(1)將鄰域窗口模板依次作用在各待融合圖像上。

(2)分別計算各對應系數的均方差。

(3)利用局部均方差融合規則進行融合處理。

在計算對應系數均方差時應先計算對應各層各方向上系數的均值，均值的計算如式(4)所示:

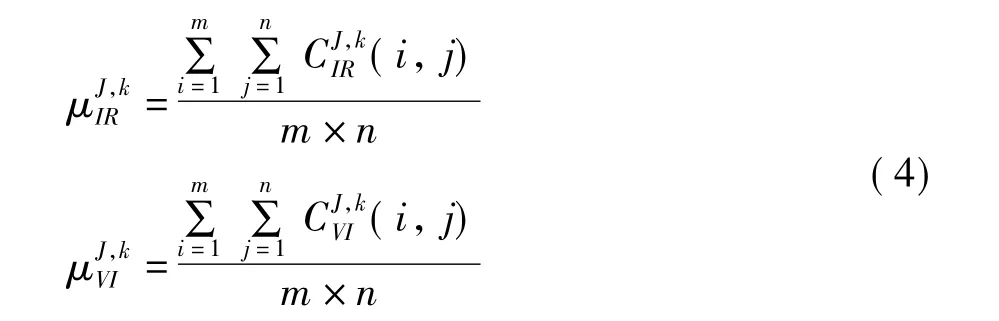
然后計算各對應系數的均方差，局部均方差的表達式如式(5)所示:

4 實驗仿真與分析

為驗證融合算法的有效性，本文采用一組同一場景可見光圖像與紅外圖像作為測試圖，來測試基于NSCT融合方法的性能并與拉普拉斯金字塔(LP)融合方法［6］、離散小波(DWT)融合方法［7］、輪廓波變換(CT)融合方法［8］進行對比。這些圖像被分解成3層且方向分別為2－2－3的子帶，采用的模板窗口。

在圖5(a)～圖5(b)中，IR圖像為紅外圖像，VI圖像為同一場景的可見光圖像。圖5(c)～圖5(f)分別是由拉普拉斯金字塔融合法、離散小波融合法、輪廓波變換融合法和本文所提出的融合方法所得到的融合圖像。這些融合圖像比原圖像的任何一幅都要好且都是比較清晰的。

為了更好地對融合算法的性能進行客觀評價，本文采用6個客觀評價指標來比較用4種不同融合方法所得到的實驗結果。這6種客觀評價指標分別為標準差(σ)、信息熵(Entropy)、均方根誤差(RMSE)、互信息(MI)、文獻［9］、［10］提出的一種通過綜合比較兩幅圖像間亮度、對比度、結構3方面信息來確定它們相似程度的客觀圖像質量評價指標SSIM因子以及Xydeas［11］提出的Q因子。紅外圖像與可見光圖像融合結果的客觀評價指標對比如表1所示，圖6為4種融合方法得到的評價指標歸一化后的客觀評價曲線，縱坐標表示各對應參數指標的值，橫坐標是為對比各融合指標便于讀者觀察所設置的，沒有實際意義。

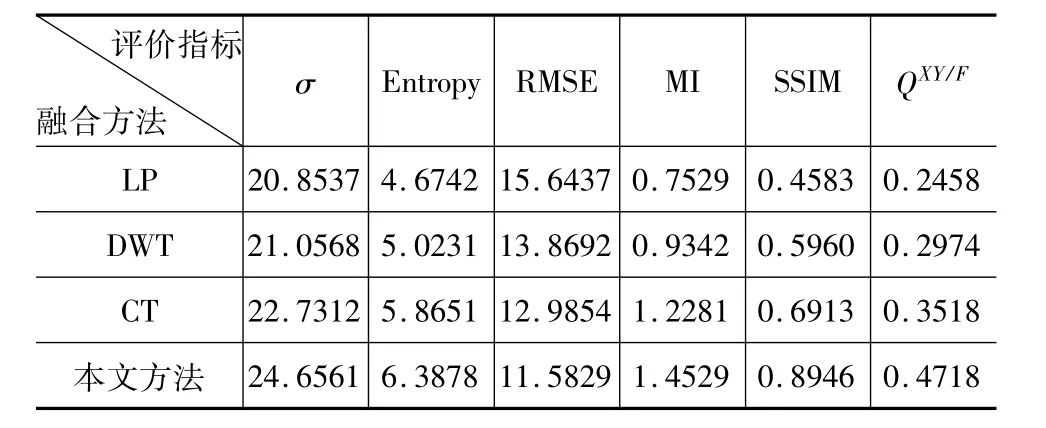
表1 紅外與可見光圖像融合結果性能評價

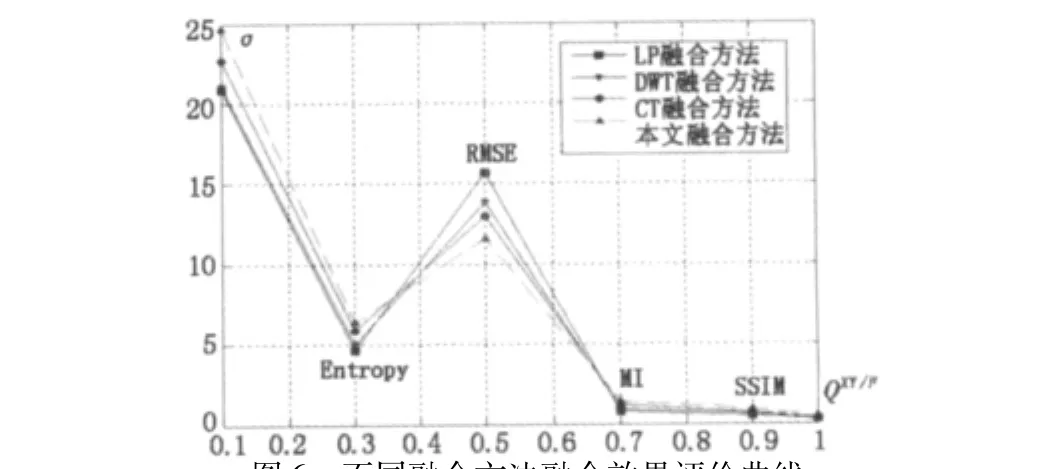
圖6 不同融合方法融合效果評價曲線

從主觀視覺效果上分析，LP融合方法所得融合圖像邊緣信息較模糊，亮點目標也不太清楚;DWT融合方法和CT融合方法所得融合圖像中引入了比較明顯的“虛影”;而采用本文提出的融合算法得到的融合圖像視覺效果相對較好，更好地保留了源圖像中的邊緣、紋理信息，“虛影”也得到了比較好的抑制。

從客觀效果評價上分析，由表1可以看出本文所用融合方法中 σ，Entropy，MI，SSIM 和 Q因子都是最大的，且RMSE是最小的。可以從圖6各指標的對比中清晰地看出來。所以由本文所提出的基于NSCT變換與局部區域融合規則相結合的紅外與可見光圖像融合方法所得到的融合圖像是所給方法中最好的。

5 結束語

NSCT在圖像處理中作為一種新的多尺度幾何分析方法，應用到圖像融合領域中，能夠為融合圖像提供更為豐富的信息，有效降低因配準誤差對融合性能的影響以及因循環平移所產生的Pseudo-Gibbs效應，還能夠比較方便地計算各子帶圖像之間的對應關系，利于融合運算的實現。本文提出的基于NSCT與局部區域融合規則的紅外與可見光圖像融合算法在保留圖像邊緣和紋理信息上都相對優于其他融合方法。同時，這一方法在其他領域也可能得到廣泛的應用，諸如遙感、戰場監視、目標跟蹤、機器視覺和醫學分析等。

［1］ Wang Hong，Jing Zhongliang，Li Jianxun．A new image fusionmethod based on target area．［J］．Chinese Journal of Lasers，2005，(3):351 －355．(in Chinese)王宏，敬忠良，李建勛．一種基于目標區域的圖像融合新方法［J］．中國激光，2005，(3):351 －355．

［2］ Liu Songtao，Zhou Xiaodong．Recent development of image fusion techniques［J］．Laser ＆ Infrared，2006，36(8):627 －631．(in Chinese)劉松濤，周曉東．圖像融合技術研究的最新進展［J］．激光與紅外，2006，36(8):627 －631．

［3］ Do M N，VetterliM．The contourlet transform:An efficient directionalmultiresolution image representation［J］．IEEE Transactions on Image Processing，2005，14(12):2091－2106．

［4］ Bui T D，Chen G．Translation-invariant denoising using multiwavelets［J］．IEEE Transactions on Signal Processing，1998，46(12):3414 －3420．

［5］ Da Cunha A L，Zhou J，Do M N．The nonsubsampled contourlet transform:Theory，design，and applications［J］．IEEE Transactions on Image Processing，2006，15(10):3089－3101．

［6］ Chen Hao，Wang Yanjie．Research on image fusion algorithm based on laplacian pyramid transform［J］．Laser＆，2009，39(4):439 －442．(in Chinese)陳浩，王延杰．基于拉普拉斯金字塔變換的圖像融合算法研究［J］．激光與紅外，2009，39(4):439 －442．

［7］ Yang Bo，Jing Zhongliang．Image fusion algorithm based on the quincunx-sampled discrete wavelet frame［J］．Automatica Sinica，2010 ，(1):12 －22．(in Chinese)楊波，敬忠良．梅花形采樣離散小波框架圖像融合算法［J］．自動化學報，2010，(1):12－22．

［8］ Zheng Jing，Zheng Yongguo．An image fusion method based on contourlet transform ［J］．Information Technology ＆ Informatization，2011，(2):37 －40．(in Chinese)鄭靜，鄭永果．一種基于Contourlet變換的圖像融合方法［J］．信息技術與信息化，2011，(2):37 －40．

［9］ Wang Z，Bovik A C，Sheikh H R，et al．Image quality assessment:From error visibility to structural similarity［J］．IEEE Transactions on Image Processing，2004，13(4):600－612．

［10］ Xu Yunsheng，Yin Dong．An image quality assessment algorithm based on contourlet transform［J］．Electronic Technology，2010，(7):23 －26．(in Chinese)徐云生，尹東．一種基于Contourlet變換的圖像質量評價算法［J］．電子技術，2010，(7):23 －26．

［11］ Xydeas C S，Petrovic V．Objective image fusion performance measure［J］．Electronics Letters，2000，36(4):308－309．