動生電動勢與暫態過程
付超杰
(周口師范學院 物理與電子工程系,河南 周口 466000)
0 引言
法拉第定律說明只要閉合電路的磁通有變化,就有感應電動勢。感應電動勢分為動生電動勢和感生電動勢。通常把磁場不隨時間變化而閉合電路的整體或局部在運動而產生的感應電動勢叫動生電動勢。動生電動勢的原理、大小和方向是怎么規定的,導體桿的動生電動勢的大小有一變化過程,這過程又是怎樣的呢?電感中的電流都不能發生突變而是隨時間按指數規律變化,指數規律變化的暫態過程存在于上述感生電動勢起關鍵作用的動態電路中。下面,我們將用經典分析法求解導體桿動生電動勢的暫態過程。
1 動生電動勢
為了研究動生電動勢的暫態過程,需要知道動生電動勢的成因及其公式,由此確定產生的感應電動勢是動生電動勢還是感生電動勢,以及是哪部分產生的及產生動生電動勢的大小。
1.1 動生電動勢的成因
圖1 ab棒在磁場中運動
1.2 動生電動勢的計算
動生電動勢原則上有兩種計算方法。
(1)用洛倫茲力公式及電動勢的定義推出的ε動=?(—v×—B)·—dl計算,先在導體上選取線元—dl,再由此計算線元處速度和磁場強度,而積分便可得動生電動勢。
(2)利用法拉第定律計算,有兩種可能。
①閉合電路整體或局部在恒定磁場中運動,根據運動情況求出閉合電路的磁通φ與t的關系,求微商dφ/dt便得動生電動勢ε。②當有一段不閉合導線在磁場中運動時,可假想一條曲線與不閉合導線組成閉合曲線,根據法拉第定律求閉合曲線動生電動勢。又因為所補曲線不動及磁場不變,ε即為所求不閉合曲線的動生電動勢[2]。另外,電磁感應而產生的動生電動勢具有相對性[3]。
2 暫態過程
當電路的結構、元件參數和激勵一定時,電路的工作狀態也就一定,且電壓和電流為一穩定的值,此時電路所處的工作狀態就稱為穩態。當電路從一種穩態轉變到另一種新的穩態時,往往需要一定的時間,電路在這段時間內所經歷的過程即為暫態過程。電路變化過程中的任一狀態都可稱為暫態。對暫態過程,一方面,我們要充分利用電路的暫態過程來實現振蕩信號的產生、信號波形的改善和變換、電子繼電器的延時動作等;另一方面,又要防止電路在暫態過程中可能產生的比穩態時大得多的電壓或電流現象。故進行暫態分析就是要充分利用電路的暫態特性來滿足技術上對電氣線路和電氣裝置的性能要求,同時又要盡量防止暫態過程中的過電壓或過電流現象[4]。
3 動生電動勢的暫態過程分析
暫態分析就是要分析在激勵源作用下,或者在電路內部儲能的作用下,電路中各部分的電壓和電流隨時間變化的規律。下面就以平行金屬導軌上導體桿產生的動生電動勢的暫態過程作出分析,并導出求動生電動勢的簡易方法。
圖2裝置中,PQ長度為l,導體的一端連接電阻R。整個裝置放在均勻磁場—B中,—B與導軌所在平面垂直。設桿以初速度v0向右運動,忽略電阻以外的電阻及導軌和桿之間的摩擦力。ε0為恒定電源電動勢,根據以下幾種情況計算導體桿的動生電動勢。

圖2 PQ棒在均勻磁場中運動
3.1 動生電動勢的零狀態響應
桿的初速度v0=0,桿中的初始電動勢為零。設開關閉合時t=0,求t≥0時導體桿的動生電動勢。
設t≥0時,任一時刻導體桿的速度為v(t),則動生電動勢大小為ε(t)=Blv(t)。根據安培定律及I=和牛頓第二定律可得微分方程:mR+B2l2v=Blε0;v(0+)=0利用分離變量法解次微分方程得:v(t)=(1-e),從而得桿的動生電動勢為:ε(t)=Blv(t)=ε0(1-e)。
當t趨向于無窮時,ε(t)=ε(∞)=ε0為動生電動勢的穩態值,則上式可寫為ε(t)=ε0(1-)。τ稱為回路的時間常數。
ε(t)的變化曲線如圖3所示。可得,動生電動勢在t=0時不能發生突變。
從電路的角度來看,暫態過程中動生電動勢可視為穩態分量和暫態分量相加而得。當動生電動勢達到穩態值時,電路的暫態過程隨即終止。
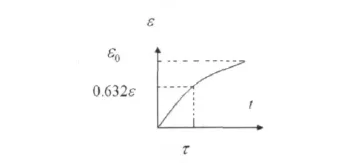
圖3 動生電動勢的零狀態響應曲線
3.2 動生電動勢的零輸入響應
設此種情況下電源電動勢ε0=0,開關k是閉合的,在時間t=0時給桿一向右的初速度v0。這時可建立速度的微分方程mR+B2l2v=0;v(0+)=v0。
解得動生電動勢為ε(t)=Blv0=Blv(0+)當t=τ時,ε(t)=ε(τ)=0.368Blv0,即τ的物理意義是動生電動勢的值減小到初始值的36.8%所需要的時間。總之,τ可看作暫態過程的“時間尺度”,從理論上講,電路只有經過t=∞的時間才能達到穩定。但是,由于指數曲線開始變化快,而后逐漸減慢,所以,實際上經過t=5τ時間,就足可認為達到穩態了。ε (τ)的變化曲線如圖4所示。
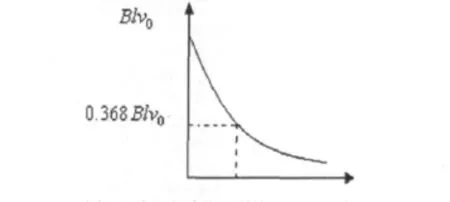
圖4 動生電動勢的零輸入響應曲線
3.3 動生電動勢的全響應
設在此種情況下ε0≠0,并在t=0時給桿一初速度v0使之向右運動,求t≥0時桿中的動生電動勢。可列出關于速度的微分方:mR+B2l2v=Blε0v(0+)=v0解得動生電動勢ε0(1-)+Blv(0+);前為零狀態響應,后為零輸入響應。則全響應的曲線應是零狀態響應曲線與零輸入曲線的疊加。上式可改寫為ε(t)=(Blv0-ε0)+ε0,可知全響應曲線仍按指數規律變化,只是它的最大值為 ε0,最小值是趨近于Blv0。改后式的第一項為衰減指數函數,t趨于無窮大時趨于零,為暫態分量;第二項為穩態分量,即全響應=暫態分量+穩態分量。
4 求動生電動勢的三要素法
據以上分析知動生電動勢的響應是由穩態分量和暫太分量兩部分相加而得:ε(t)=ε(∞)+[ε(0+)-ε(∞)]t,式中ε(∞)和ε(0+)分別為動生電動勢的穩態值和初始值,因此,只要求得以上三個值即可列出動生電動勢隨時間的變化關系式,而不用再求解微分方程,故稱此法為求解動生電動勢的三要素法[5]。

圖5 動生電動勢的全響應曲線
5 結語
本文根據動生電動勢和暫態過程分析得出動生電動勢的兩種求法,利用一階微分方程解法對動生電動勢的幾種響應進行了分析,得出電路的響應是由暫態分量和穩態分量兩部分相加而得,且動生電動勢的暫態分量按指數規律變化。從而得出用三要素法求動生電動勢:無論是電路的零狀態、零輸入或全響應,輸入量不論是恒定電源或恒力均可用三要素法方便的求出動生電動勢或速度隨時間的變化規律[6]。三要素法給我們提供了一種研究暫態過程的簡便方法,在以后的解題中,我們應首先考慮是否能用三要素法解題。
[1]顏琳.王小云.全秀娥.動生電動勢的產生機理[J].吉首大學學報,2007,28(1):71-72.
[2]梁燦斌,秦光戎,梁竹健.電磁學[M].北京:高等教育出版社,2004.
[4]孫國耀.動生電動勢的相對性[J].中山大學學報,2005,44:166-167.
[5]蘇民.動生電動勢與暫態過程[J].殷都學刊,1994,(2):30-32.
[6]房淑芬.談動生電動勢[J].遼寧師專學報,2000,2 (4):31-32.

