不可逆矩形循環的功率和效率特性

劉長鑫，陳林根，戈延林，孫豐瑞

（海軍工程大學動力工程學院，武漢 430033）

0 引言

自從有限時間熱力學［1－3］被用于實際熱機的性能分析和優化研究以來，目前已經取得了一系列成果。例如Mozurkewich等［4］和Hoffman等［5］用最優控制理論優化Otto循環和Diesel循環的活塞運動規律，Aizenbud等［6］和陳林根等［7］將活塞式加熱氣缸中活塞最優運動規律用到了內燃機循環分析中，Orlov等［8］導出了內燃機的功率效率極限，Angulo-Brown等［9］和陳林根等［10］建立了一類考慮有限時間特性和摩擦損失的Otto循環和Diesel循環模型，Klein［11］考慮了傳熱對Otto循環和Diesel循環特性的影響，陳林根等［12－13］導出了存在傳熱損失時Diesel循環和Otto循環的功率效率特性，鄭彤等［14］導出了存在傳熱和摩擦損失時Dual循環的功率效率特性，Qin等［15］給出了一類不可逆往復式熱機普適的功率效率特性，Al-Hinti等［16］研究了在不同傳熱模型中Diesel循環的性能，劉暢等［17］建立了考慮存在傳熱損失的內可逆工質恒比熱Meletis-Georgiou（MG）循環模型并進行了分析和優化。特別是Ferreira Da Silva［18］提出了一種由定容吸熱、定壓吸熱、定容放熱和定壓放熱4個熱力過程組成的新型循環（其p-V圖呈矩形，故稱為矩形循環）；并應用經典熱力學理論導出了該循環的輸出功率和效率公式，當存在傳熱、摩擦和熱漏等損失時，分析矩形循環的有限時間熱力學特性可指導實際應用。

本文將在前人工作的基礎上建立具有有限時間特性、存在摩擦及傳熱損失的空氣標準矩形循環模型，并研究其功率和效率特性。

1 循環模型和性能分析

圖1為空氣標準矩形循環模型圖，圖1（a）為壓力（p）與體積（V）關系圖，其中1→2為定容吸熱過程，2→3為定壓吸熱過程，3→4為定容放熱過程，4→1為定壓放熱過程。圖1（b）為溫度（T）與熵（S）關系圖。

圖1 矩形循環模型

設吸熱過程和放熱過程的溫度分別按等速率變化：

式中：T為溫度；t為時間；K1和K2為常數。

對式（1）積分有：

式中：t1和t2分別為加熱和冷卻時間。

因此，循環周期τ為：

對于整個循環，輸出功為：

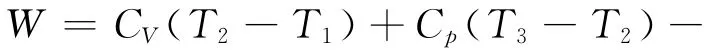
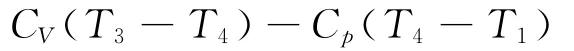
式中：CV和Cp分別為等容熱容和等壓熱容，即等容和等壓比熱容與質量流量之積。

因此功率為：

在1→3過程中，工質吸收的熱量為：

理想的矩形循環不存在不可逆損失，但對于實際矩形循環，工質和氣缸間的不可逆傳熱損失和活塞摩擦損失不能忽略。

把諸種因素對燃燒的影響用燃燒過程的當量放熱量α表示；將壓縮、燃燒及其后的膨脹過程中氣缸與外界的熱交換全部集中于燃燒過程，用－β（T3＋T1）表示。則在燃燒過程中傳給工質的熱量可寫為［8，11－13］：

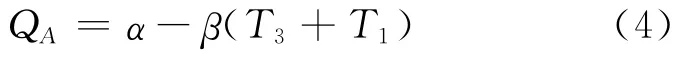
式中：α為膨脹過程中當量放熱量，常數；β為傳熱損失系數，常數。

對空氣標準矩形循環過程1→2，2→3，3→4和4→1，有：

式中：p為壓力；V為體積。

定義循環膨脹比rl：

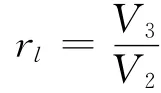
則由式（5）得：

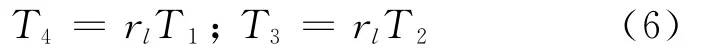
由式（3）、式（4）和式（6）可得：

將式（6）和式（7）代入式（2）中，得出功率為：

活塞運動存在摩擦損失，按照Angulo-Brown等［9］和陳林根等［10］對有限時間特性和摩擦損失的Otto循環和Diesel循環的處理方法，設摩擦力與速度呈線性關系。即：

式中：μ為考慮全部損失的摩擦系數；x為活塞的位移。

因此，損失功率為：

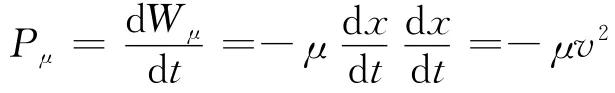
式中：x2為在最小容積處的活塞位置；Δt12為功率沖程消耗的時間。

則循環凈功率輸出為：

循環的熱效率為：

或者：

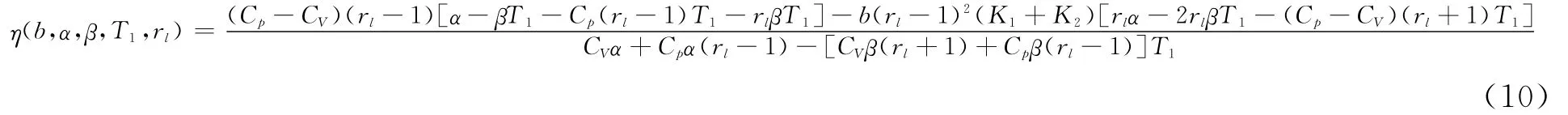
2 數值算例

算例計算的目的是利用數據分析摩擦損失對矩形循環的功率和效率的影響，以及當量放熱量α，傳熱損失系數β和初始溫度T1對矩形循環的功率和效率的影響。

由氣體摩爾數和摩爾熱容，CV＝0.716 5 J／K，Cp＝1.003 1 J／K。由t1＝t2＝τ／2＝16.6 ms（τ＝33.33 ms［4］）和對應的溫度值反算出K1＝8.128μs／K，K2＝18.67μs／K。

依文獻［4］取x2／Δt12＝0.6m／s，摩擦損失b的取值范圍為0～65 W。根據Angulo-Brown［9］和Klein［11］的方法，當量放熱量α＝2500～4000kJ／kg，傳熱損失系數β＝0.3～1.8 kJ／（kg·K）和初始溫度T1＝300～400 K。

2.1 摩擦損失的影響

為了分析摩擦損失對矩形循環的功率和效率的影響，摩擦損失b分別取0 W，32.5 W和65.0 W，算例取值見表1。

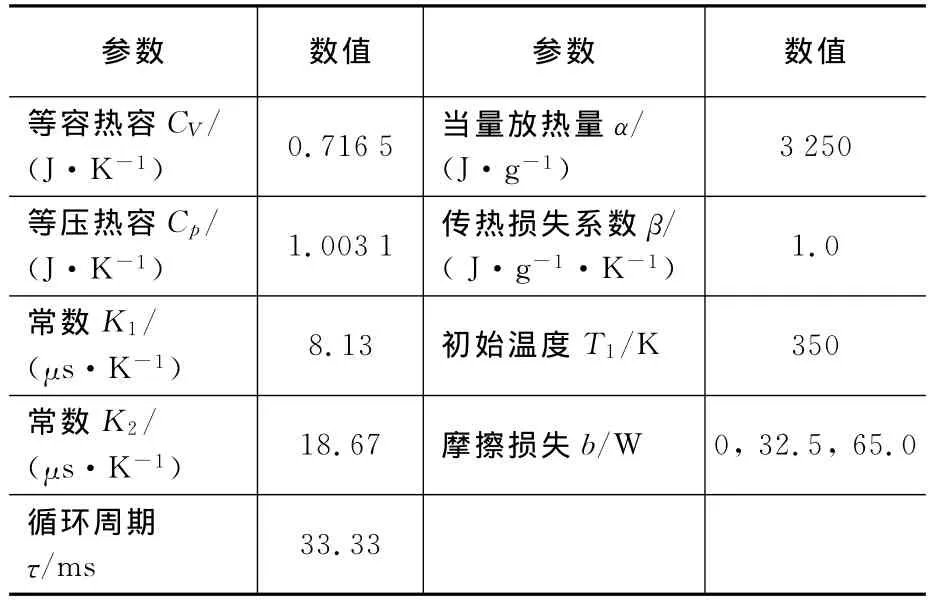
表1 用于分析摩擦損失影響的取值參數數值

利用表1所列值，結合式（8）可以得到矩形循環的功率與膨脹比關系（圖2），結合式（10）得到效率與膨脹比關系（圖3）；結合式（9）可以得到功率-效率特性（圖4）。

圖2 功率－膨脹比關系

圖3 效率－膨脹比關系

以摩擦損失b取32.5 W時的圖線為例。由圖2可知，該算例的最大輸出功率為Pmax＝4.117 5 k W，對應的最佳膨脹比為rl，P＝2.120 0；由圖3可知，算例的最高效率為ηmax＝0.117 4，其對應的最佳膨脹比為rl，η＝2.020 0。當圖2取得最大輸出功率時，對應圖3的效率為ηP＝0.117 0；當圖3取得最高效率時，對應圖2的輸出功率為Pη＝4.102 6 k W。這些結果也可以從圖4中得到印證。

圖4 功率－效率特性

圖2中功率隨膨脹比變化呈類拋物線型，并且增加摩擦損失會導致功率減小；圖3中效率隨膨脹比變化呈類拋物線型，增加摩擦損失會導致效率降低；但是摩擦損失的變化不改變曲線的形狀。由圖4可見，功率－效率特性曲線呈回原點的扭葉型，摩擦對功率和效率特性的影響較小。

2.2 傳熱損失系數、當量放熱量和初始溫度的影響

為了分析β、α和T1各自對矩形循環功率和效率特性的影響，每一個因素取三個值，見表2。

表2 用于分析α，β，T1影響的取值

圖5是傳熱損失系數對功率－效率特性的影響，圖中給出了β取0.3，1.0和1.8 kJ／（kg K）時矩形循環的功率－效率特性。由圖可見：對于β不同的取值，矩形循環的最大功率Pmax在5.170 4～3.120 7 k W之間變化，對應的效率ηP為0.146 7～0.088 2；矩形循環的最高效率ηmax在0.147 2～0.088 2之間變化，對應的功率Pη為5.152 6～3.112 4 k W。進一步分析可以得到：最大功率對應的膨脹比rl，P為2.66～1.72；最高效率對應的膨脹比rl，η為2.51～1.66。

圖6是當量放熱量對功率－效率特性的影響。圖中給出了α取2 500，3 250和4 000 kJ／kg時矩形循環的功率－效率特性。由圖可見：對于α不同的取值，矩形循環的最大功率Pmax在3.579 6～4.529 6 k W之間變化，對應的效率ηP為0.100 2～0.129 4；矩形循環的最高效率ηmax在0.100 5～0.129 8之間變化，對應的功率Pη為3.568 8～4.512 0 kW。

進一步分析可以得到：最大功率對應的膨脹比rl，P為1.86～2.33；最高效率對應的膨脹比rl，η為1.80～2.21。

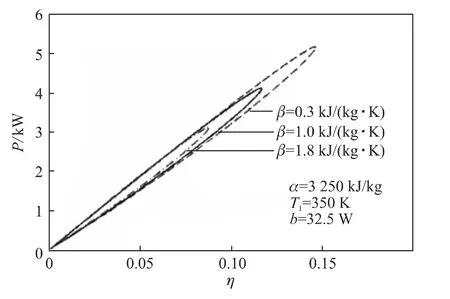
圖5 β對功率－效率特性的影響

圖6 α對功率－效率特性的影響

圖7是初始溫度對功率－效率特性的影響。圖中給出了T1取300，350和400 K矩形循環的功率－效率特性。由圖可見：對于T1的不同取值，最大功率Pmax在4.424 9～3.845 4 k W之間變化，對應的效率ηP為0.126 2～0.108 7；矩形循環的最高效率ηmax在0.126 7～0.109 0之間變化，對應的功率Pη為4.408 0～3.830 7 k W。進一步分析可以得到：最大功率對應的膨脹分別比rl，P為2.28～1.98；最高效率對應的膨脹比rl，η為2.16～1.90。

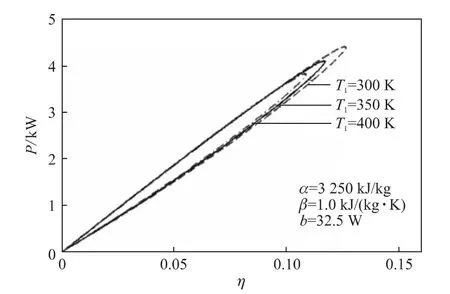
圖7 T 1對功率－效率特性的影響

分析結果表明：和摩擦損失b一樣，β、α和T1的變化對功率效率特性曲線的形狀影響不大，但隨著α的增大，b、β和T1的減小，循環能達到的最大功率和最高效率增大。

3 結語

實際熱機的有限時間熱力學模型是理解和優化熱機性能的重要工具。本文建立了考慮有限時間特性、存在摩擦及傳熱損失時的空氣標準矩形循環模型，導出了循環的功率及效率解析式，由數值計算得到了對應于最大功率和最高效率的最佳膨脹比，主要結論有三點。

1）功率及效率隨膨脹比的變化曲線呈類拋物線型，功率－效率特性曲線呈回原點的扭葉型；摩擦、傳熱損失系數、當量放熱量和初始溫度的變化均不改變關系曲線的形狀。

2）摩擦的變化對功率－效率特性的影響較小，當量放熱量、傳熱損失系數和初始溫度的變化對功率效率特性影響較大。

3）摩擦的增大會導致功率及效率的下降；當量放熱量的增大，摩擦、傳熱損失系數和初始溫度的減小，會使循環的最大功率和最高效率增大。

［1］ Bejan A.Entropy generation minimization：The new thermodynamics of finite-size device and finite-time processes［J］.J.Appl.Phys，1996，79（3）：1191-1218.

［2］ Chen L，Wu C，Sun F.Finite time thermodynamic optimization or entropy generation minimization of energy systems［J］.J.Non-Equilib.Thermodyn，1999，24（4）：327-359.

［3］ 陳林根.不可逆過程和循環的有限時間熱力學分析［M］.北京：高等教育出版社，2005.

［4］ Mozurkewich M，Berry R S.Optimal paths for therm-odynamic systems：the ideal Otto cycle［J］.J.Appl.Phys，1982，53（1）：34-42.

［5］ Hoffman K H，Watowich S J，Berry R S.Optimal paths for thermodynamic systems：The ideal Diesel cycle［J］.J.Appl.Phys，1985，58（6）：2125-2134.

［6］ Aizenbud B M，Band Y B，Kafri O.Optimization of a model internal combustion engine［J］.J.Appl.Phys，1982，53（3）：1277-1282.

［7］ Chen L，Sun F，Wu C.Optimal expansion of a heated working fluid with linear phenomenological heat transfer［J］.Energy Convers.Mgmt，1998，39（3／4）：149-156.

［8］ Orlov V N，Berry R S.Power and efficiency limits for internal combustion engines via methods of finite-time thermodynamics［J］.J.Appl.Phys，1993，74（10）：4317-4322.

［9］ Angulo-Brown F，Fernandez-Betanzos J，Diaz-Pico C A.Compression ratio of an optimized Otto-cycle model［J］.Eur.J.Phys，1994，15（1）：38-42.

［10］ 陳林根，林俊興，孫豐瑞.摩擦對空氣標準Diesel循環功率效率特性的影響［J］.工程熱物理學報，1997，18（5）：533-535.

［11］ Klein S A.An explanation for observed compression ratios in internal combustion engines［J］.Trans.ASME J.Engng.Gas Turbine Pow，1991，113（4）：511-513.

［12］ Chen L，Zen F，Sun F et al.Heat transfer effects on the net work output and power as function of efficiency for air standard Diesel cycle［J］.Energy，1996，21（12）：1201-1205.

［13］ Chen L，Wu C，Sun F et al.Heat transfer effects on the net work output and efficiency characteristics for an air standard Otto cycle［J］.Energy Convers.Mgnt，1998，39（7）：643-648.

［14］ 鄭彤，陳林根，孫豐瑞.不可逆Dual循環的功率效率特性［J］.內燃機學報，2002，20（5）：408-412.

［15］ Qin X，Chen L，Sun F.The universal power and efficiency characteristics for irreversible reciprocating heat engine cycles［J］.Eur.J.Phys，2003，24（4）：359-366.

［16］ Al-Hinti I，Akash B，Abu-Nada E，et al.Performance analysis of air-standard Diesel cycle using an alternative irreversible heat transfer approach［J］.Energy Convers.Manage，2008，43（15）：2019-2031.

［17］ 劉暢，陳林根，孫豐瑞.內可逆工質恒比熱Meletis-Georgiou循環有限時間熱力學建模與性能優化［J］.熱力透平，2011，40（2）：115-120.

［18］ Ferreira Da Silva M F.Some considerations about thermodynamic cycles［J］.Eur.J.Phys，2012，33（1）：13-42.