利用堆排序優化路徑搜索效率的分析

孫玉昕,章 瑾

(武漢工程大學計算機與科學學院，湖北 武漢 430074)

0 引 言

路徑搜索的核心思想是利用計算機的處理能力，準確高效地在網絡中任意兩個或多個節點之間尋找出最佳路徑.路徑搜索算法在計算機工程中有著廣泛的應用價值，比如地理信息系統、位置服務、智能交通、智能機器人等領域[1].在工程實踐中，路徑搜索的時間效率和空間效率是判斷算法的優劣重要指標[2].啟發式搜索和盲目搜索相比，可省略大量無謂的搜索路徑，已能夠極大提高搜索效率，但當面臨百萬節點的復雜網絡拓撲時，啟發式搜索算法的搜索耗時將會呈指數級快速增長，無法滿足需求，因此考慮引入二叉堆進行進一步的算法優化，使得搜索速度進一步提升.

1 實驗部分

1.1 算法選擇

路徑搜索的核心算法就是最短路徑算法 ,它是計算機科學與地理信息科學等領域研究的熱點.目前已知的最短路徑算法主要有 Floyd (弗洛伊德)算法、矩陣算法和Dijkstra(迪杰斯特拉)算法.其中Dijkstra算法是最為經典的最短路徑算法，其主要特點是以起始點為中心逐層外推，直到推進至終點.Dijkstra算法能確保求出最短路徑的最優解，但由于它是逐層遍歷的方式導致其效率比較低，無法滿足工程實際的需求[3].

為了滿足效率和靈活性要求，基于人工智能的啟發式搜尋法(Heuristic Search Methods)的A*算法常被應用路徑搜索[4].所謂啟發式是在Dijkstra算法基礎上，引入啟發函數(Heuristic Function)來估算當前節點與目標節點的距離，通過啟發函數的估算值不斷動態調整搜索方向.與Dijkstra算法的盲目搜索過程，A*算法的啟發式搜索方法充分利用網絡拓撲圖給出的信息來動態地調整搜索方向，因此搜索效率更高[5-6].

A*算法的核心計算公式表示為

f(n)=g(n)+h(n)

其中f(n) 是途經節點n從初始點到目標節點的路徑距離的估價函數值，g(n) 是在狀態空間中從初始節點到n節點的實際路徑距離，h(n)是從n到目標節點的距離的啟發函數.f(n)值越小則表示該結點的路徑越短[7-9].

A*算法流程圖如圖1所示.運用A*算法進行路徑搜索計算.A*算法的時間復雜度是O(n2)，n為網絡節點數量.因此，隨著網絡節點數和路徑長度的增加，A*算法的搜索耗時呈指數級的快速增長.在工程實際中，經常需要對大規模的節點進行搜索，當面臨百萬節點的復雜網絡拓撲時， A*算法的效率仍然無法滿足需求[5，7].

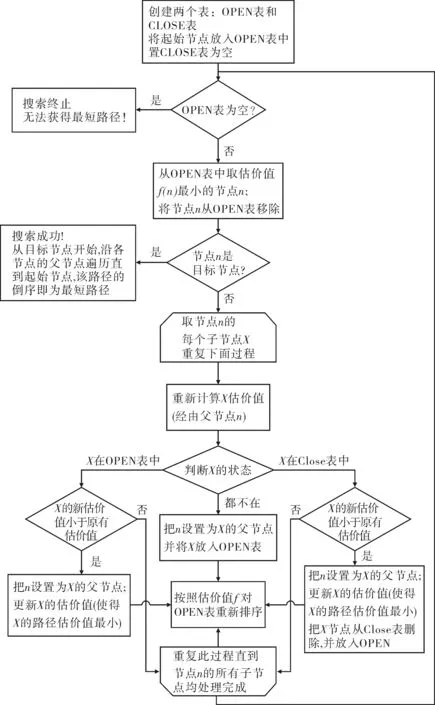
圖1 A*算法流程圖Fig.1 A* algorithm flowchart

1.2 優化分析

針對上述大規模網絡的路徑搜索需求，重點研究了應用A*算法進行路徑搜索時的效率優化問題.A*算法的數據結構的核心是兩個表：Open表(Open表中存放已計算出估計值的結點)與Closed表(Closed表存放已訪問過的結點)，并且還沒有訪問過的A*結點.Open表是A*算法訪問最頻繁的表，因為需要從Open表中取出最小的估計值，作為本次訪問節點.

大量的操作是針對Openlist列表(Openlist表存放可能成為最短路徑的隊列)進行的，重復不斷的OpenList進行節點增加，刪除，查找，按f值排序等操作.可以說Open表的數據結構設計很大程度上決定了算法的效率.最易于實現Open表數據結構是鏈表結構，采用鏈表或者哈希表的數據結構來處理Openlist.這樣算法的過程比較清晰，設計難度也較低.但是當需要處理大規模的網絡時，OpenList的列表長度會增長到有數千個節點組成.在重復對大規模的節點進行排序，搜索，操作，計算量會非常大.其中最主要的是對Openlist的排序操作，如果使用常規的排序算法如冒泡法等，需要重復不斷的遍歷整個列表，算法復雜度是O(n2)[2].

A*算法并不需要Openlist完全有序，只需要找出f值最小的節點即可，而對其他節點的位置無要求.因此采用二叉堆可滿足算法對Openlist的操作需求.

首先二叉堆是完全二叉樹，并滿足堆的特性：父節點的鍵值總是小于其子節點的鍵值.最小鍵值的節點總在堆的頂端.因此在算法中查找f值最小的節點，堆頂端的節點就是需要的節點.用一維數組來表示二叉堆時，數組中第n(n>=1)節點，其子節點位于數組的2n和2n+1的位置，其父節點位于數組n/2的位置.如圖2所示(數組下標從1開始).

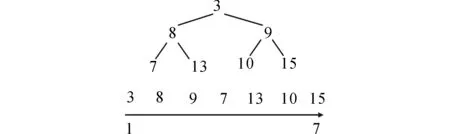
圖2 二叉堆的數組表示Fig.2 Binary heap array representation

顯然數組第1個節點就是堆頂節點，就是f值最小節點.利用二叉堆的特性，可直接獲取Open表中f值最小的節點.從openlist列表中取出f值最小的節點，需要將其從堆移除.在移除堆頂節點后，將堆的最后一個節點移動到頂點，再將新堆頂與其兩個子節點比較，如父節點比子節點大，就交換二者，直到父節點比兩個子節點的f值都低.

當向二叉堆增加節點時，可將新節點放在數組末尾.然后與其父節點比較，如果新節點的f值更低，就交換父子的位置.直到新節點不再比它的父節點低，或者這個節點已經到達頂端.在搜索過程中，節點的f值可能會改變，這時要重新對Openlist進行有序化處理：從發生改變的節點開始，將其與父節點比較，如果子節點的f值小于其父節點，就將他們交換.直到到達堆頂為止.

運用二叉堆可直接獲取Openlist的f值最小的節點，計算量與Openlist大小無關.向Openlist插入節點，刪除節點，排序操作的算法時間復雜度都是O(logn).n為Openlist的節點數.從理論分析可知，二叉堆對于大規模的A*路徑搜索是效率比較優化的算法.

2 結果與討論

應用A*算法進行最短路徑搜索，用于測試的路網模型是一個擁有100萬個節點(1000*1000)的超大型二維網格.為了網絡拓撲模型更加清晰化和結構化，網絡中的每個節點(處于邊緣的節點除外)都擁有8個不同方向的相鄰節點，節點分為兩類：可通行與不可通行.A*算法需要在網格中指定的起始節點和目標節點之間，快速搜索出一條由可通行的節點組成的而且是代價最小的通行路徑.在測試網絡中按照一定比例(30%)隨機地設置的不可通行節點，當路徑搜索遇到不可通行的節點時，是不能直接通行的，必須要繞過.

路徑代價如圖3中，節點與方向正對的四個相鄰節點之間的路徑代價為10，與斜向方向的相鄰節點的四個子節點的路徑代價為14.這樣的路網結構可以很好的模擬二維平面路網的拓撲結構和數學模型，同時盡量采用整形數值計算，降低運算難度，提高計算效率.

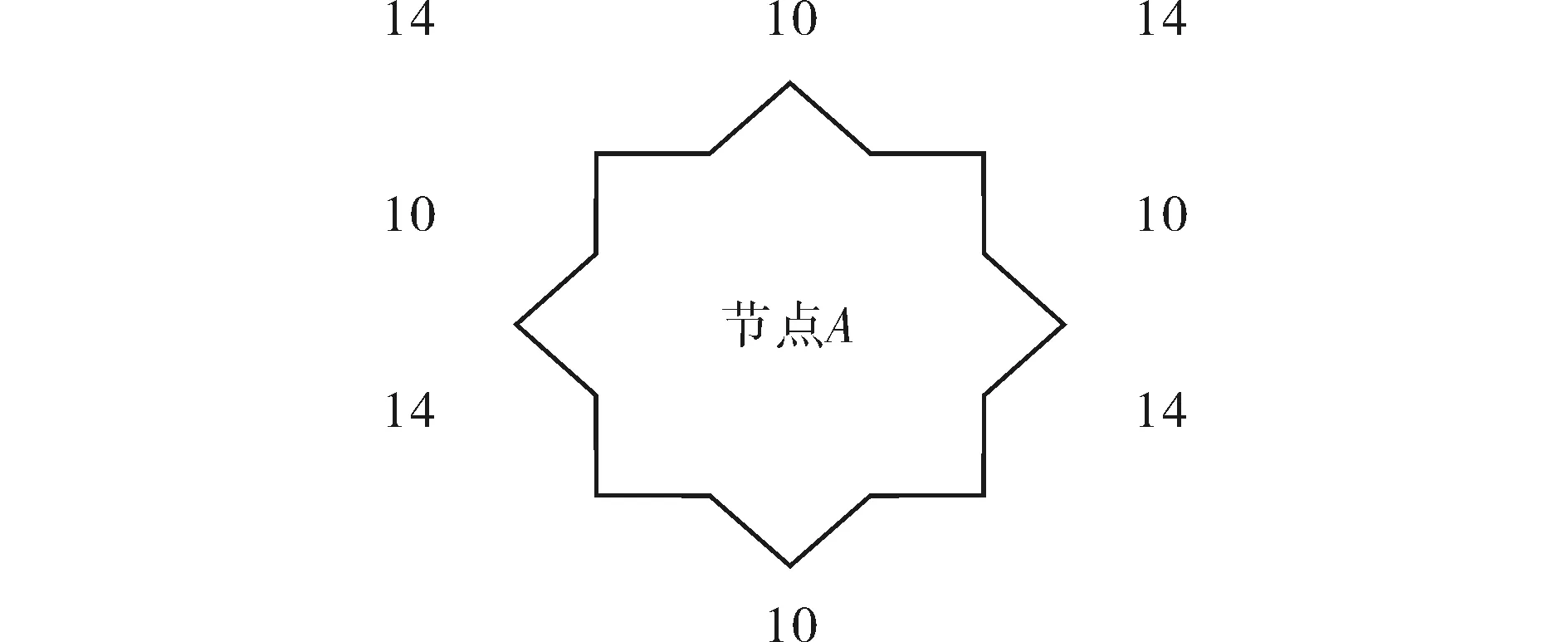
圖3 網絡結構模型Fig.3 Network structure model

A*算法中的關鍵估價函數值f(n)=g(n)+h(n)，其中g(n)表示為從節點n到起始節點s的已知最短路徑長度.H(n)標準從節點n到目標節點o的路徑估計值.估價函數f(n) =g(n) +h(n)代表經過該節點的路徑的估計值，在A*算法運行中，f(n)值越小那么此節點的路徑越好.估價函數通過判斷父節點和子節點的相對位置來進行累加計算，從起始節點開始逐步外推，直到到達目標節點位置.

對二維網絡拓撲，圖中節點由坐標(X,Y)表示，那么節點A到目標節點B的啟發函數可以用兩點間最短路徑的方法來設計，即

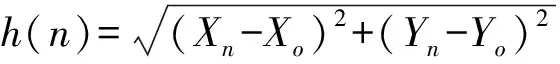
但考慮到計算機在處理開平方根運算會增大計算量，采用另外一個近似的公式取代

H(n)=abs(Xn-Xo)+abs(Yn-Yo)

其中，Xn，Yn為節點n的橫向和縱向坐標值;Xo，Yo為目標節點o的橫向和縱向坐標值.

abs()為絕對值函數.圖4為路網搜索的過程實例，圖中每個像素點代表路網拓撲中一個節點，白色點為可通行節點，黑色點為不可通行節點.深灰色點為搜索過的節點(Close表)，白色點組成的線條即為所需的最短路徑結果.

圖4 網絡搜索過程Fig.4 Road network search process

通過常規的鏈表數據結構實現的Openlist和采用二叉堆進行優化后的Openlist的算法進行多次對比分析，結果如表1和圖5所示.

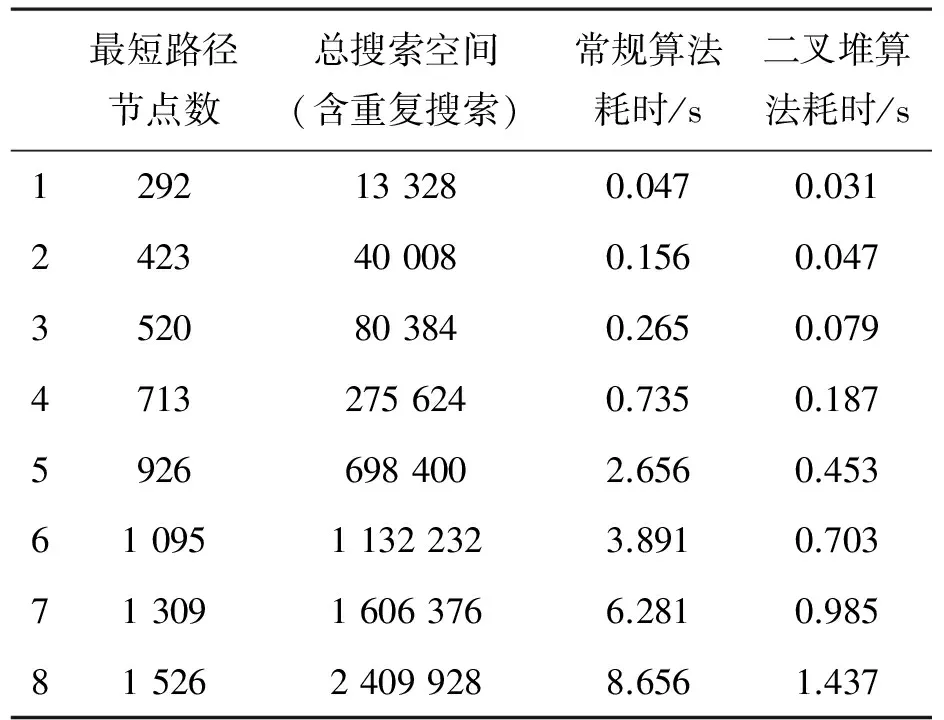
表1 引入二叉堆算法后實際耗時對比Table 1 Introduction of binary heap algorithms compare the actual time-consuming

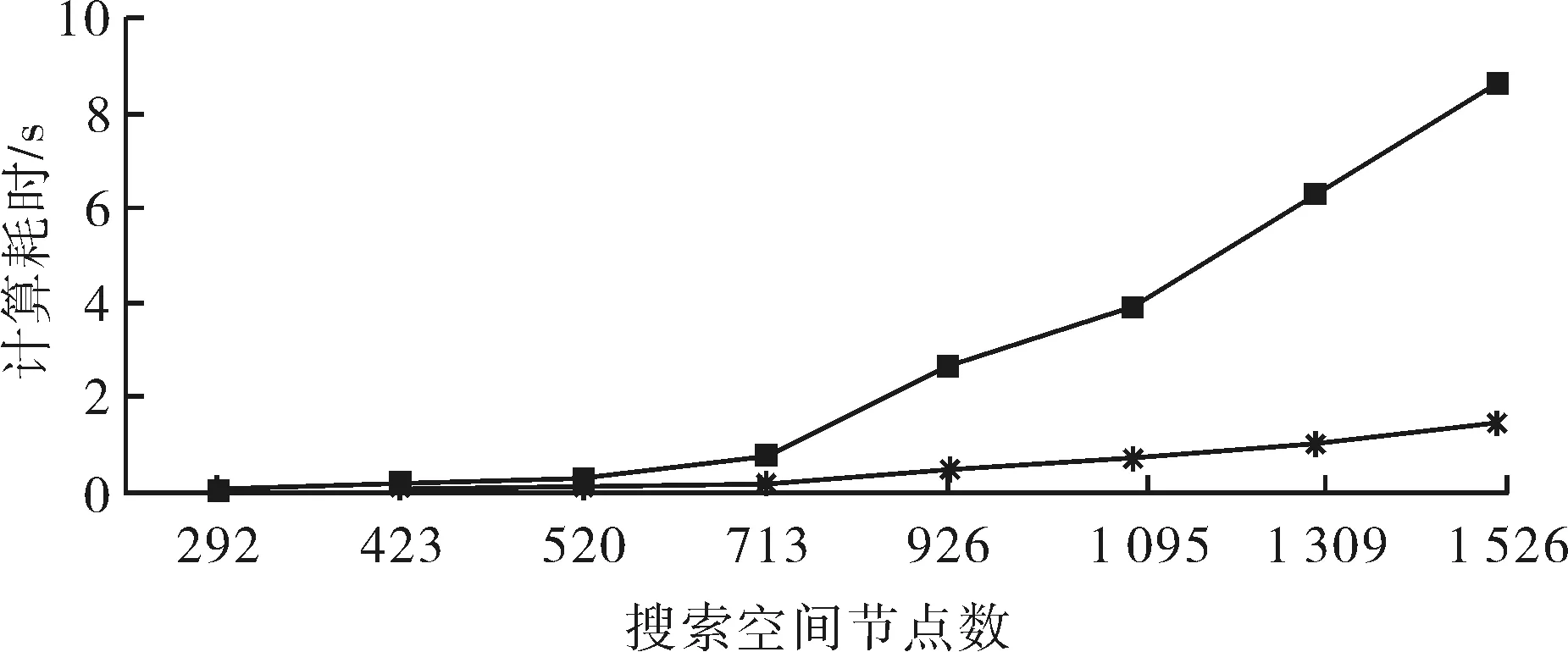
圖5 引入二叉堆算法后實際耗時對比Fig.5 Introducing binary heap algorithm actually consuming comparison chart注：

3 結 語

從兩種算法的計算量和耗時對比可知，常規算法在進行長路徑、大搜索空間的搜索時，計算時間迅速增加，而二叉堆算法則表現出良好的時間線性，沒有出現搜索時間爆炸式增長的情況.而針對數千個路徑節點，在需要搜索幾百萬的海量節點空間的情況下，應用二叉堆數據結構的A*算法具有良好的時間線性度，具備工程應用價值.

致謝

論文在資料收集和實驗數據采集過程中，得到黃珂副教授的大力支持，在此謹向她表示衷心的感謝.

參考文獻：

[1] 陳偉亞，劉芳芳.地理信息系統在水污染控制規劃中的應用[J].武漢工程大學學報，2013，35(1)：21-25.

CHEN Wei-ya, LIU Fang-fang. Applieation of geo-graphic information system teehnology in planing of water pollution control[J]. Jouranal of wuhan insti-tute of teehnology, 2013，35(1)：21-25.(in Chinese)

[2] 柳林，張繼賢，唐新明，等.LBS體系結構及關鍵技術的研究[J].測繪科學,2007,32(5)： 144-146.

LIU Lin, ZhANG Ji-xian, TANG Xin-ming, at al. LBS architecture and Research of key technologies[J]. Science of Surveying and Mapping,2007,32 (5):144-146 .(in Chinese)

[3] 顧運筠.最短路徑搜索算法的幾種優化改進[J].計算機應用與軟件，2008，25(4):246-247.

GU Yun-jun. Shortest path search algorithm several optimized and improved[J]. Computer Applications and Software,2008,25(4): 246 -247.(in Chinese)

[4] 劉浩，鮑遠律.A*算法在矢量地圖最優路徑搜索中的應用[J]. 計算機仿真,2008，25(4):253-257.

LIU Hao, BAO Yuan-lv.The application of the A*algorithm searching the optimal vector path map[J]. Computer Simulation, 2008,25(4): 253-257.(in Chinese)

[5] 陳和平，張前哨.A*算法在游戲地圖尋徑中的應用與實現[J].計算機應用與軟件,2005，22(12):118-120.

CHEN He-ping, Zhang Qian-shao. Application and Implementation of the A*algorithm pathfinding in game maps[J]. Computer Applications and Software, 2005, 22(12):118-120.(in Chinese)

[6] 史輝，曹聞，朱述龍，等.A*算法的改進及其在路徑規劃中的應用[J].測繪與空間地理信息,2009，32(6): 208-211.

SHI Hui, CAO Wen, ZHU Shu-long, et al. A*algorithm and its application in path planning[J]. Geomatics & Spatial Information,2009,32 (6): 208-211.(in Chinese)

[7] 朱福喜,傅建明.人工智能原理[M]. 武漢：武漢大學出版社，2002.

ZHU Fu-xi, FU Jian-ming. Principle of artificial intelligence[M]. Wuhan: Wuhan University press, 2002.(in Chinese)

[8] 龔劬.圖論與網絡最優化算法[M].重慶：重慶大學出版社，2009.

GONG Qu. Graph theory and network optimization algorithms[M]. Chongqing: Chongqing University Press,2009.(in Chinese)

[9] 魯統偉，林芹，李熹，等.記憶運動方向的機器人避障算法[J].武漢工程大學學報，2013，35(4)：66-71.

LU Tong-wei, LIN Qin, LI Xi, et al. Obestacle avoidance algorithm of robot based on recording moue direction. Jouranal of Wuhan instute of technology，2013，35(4)：66-71.(in Chinese)