對GUM法量塊測量不確定度評定的驗證

馮亞南，李鎖印，韓志國

(中國電子科技集團公司第十三研究所，河北石家莊 050051）

0 引言

ISO/IEC發布的Guide98-3-2008《測量不確定度表示指南》(GUM）給出了測量不確定度評定與表示的通用方法。2008年，計量指南聯合委員會(JCGM）在GUM方法的基礎上推出了補充件——采用蒙特卡洛法評定測量不確定度，將蒙特卡洛法作為對GUM方法的重要補充。我國新頒布的JJF1059.2-2012《采用蒙特卡洛法評定測量不確定度》是依據該補充件進行編制的。該規范規定了用蒙特卡洛法評定與表示測量不確定度的方法，并就GUM中未涉及的概率分布傳播的問題提供指導，擴大了測量不確定度評定與表示的適用范圍，同時該規范提供了檢查GUM法是否適用的驗證方法。

雖然GUM法在許多情況下被認為是非常適用的，但是確定是否滿足其所有應用條件并不是一件容易的事。由于MCM的適用范圍比GUM法更廣泛，建議用MCM及GUM法兩種方法，并對結果進行比較。如果比較結果較好，則GUM法適用于此場合及今后足夠類似的情形。否則，應考慮采用MCM或者其它合適的替代方法。GUM法若明顯適用，則依然是不確定度評定的主要方法。

1 驗證步驟

下面以量塊校準為例，詳細介紹用蒙特卡洛法驗證GUM法結果的具體步驟。

1.1 測量模型

由二等量塊作為標準，用電腦量塊比較儀校準三等量塊時，經測量可得到標準量塊和被測量塊的長度差d。設ls和l為標準量塊和被測量塊在20℃時的長度；ts和t為檢定時標準量塊和被測量塊的溫度；αs和α為標準量塊和被測量塊的線膨脹系數，則標準量塊和被測量塊的長度差可直接表示為

用電腦量塊比較儀校準量塊時，由于量塊存在一定的長度變動量，測點位置不同，會對d的測量數據產生影響。δs(ΔPs）和δ(ΔP）為測點偏離標準量塊和被測量塊中心所產生的誤差，則輸出量l的公式變為

1.2 測量數據

對標稱長度為100 m的量塊中心長度進行測量，重復測量10次，測得被測量塊與標準量塊中心長度差算術平均值為 -0.40μm，計算實驗標準偏差為0.021μm。

1.3 采用GUM法對量塊測量不確定度進行評定

JJG146-2011量塊檢定規程中給出了采用GUM法對量塊測量不確定度的評定，我們參照量塊規程中給出的方法，對測量的100 mm量塊測量不確定度進行評定。數學模型采用公式 (4）的一階泰勒級數近似。

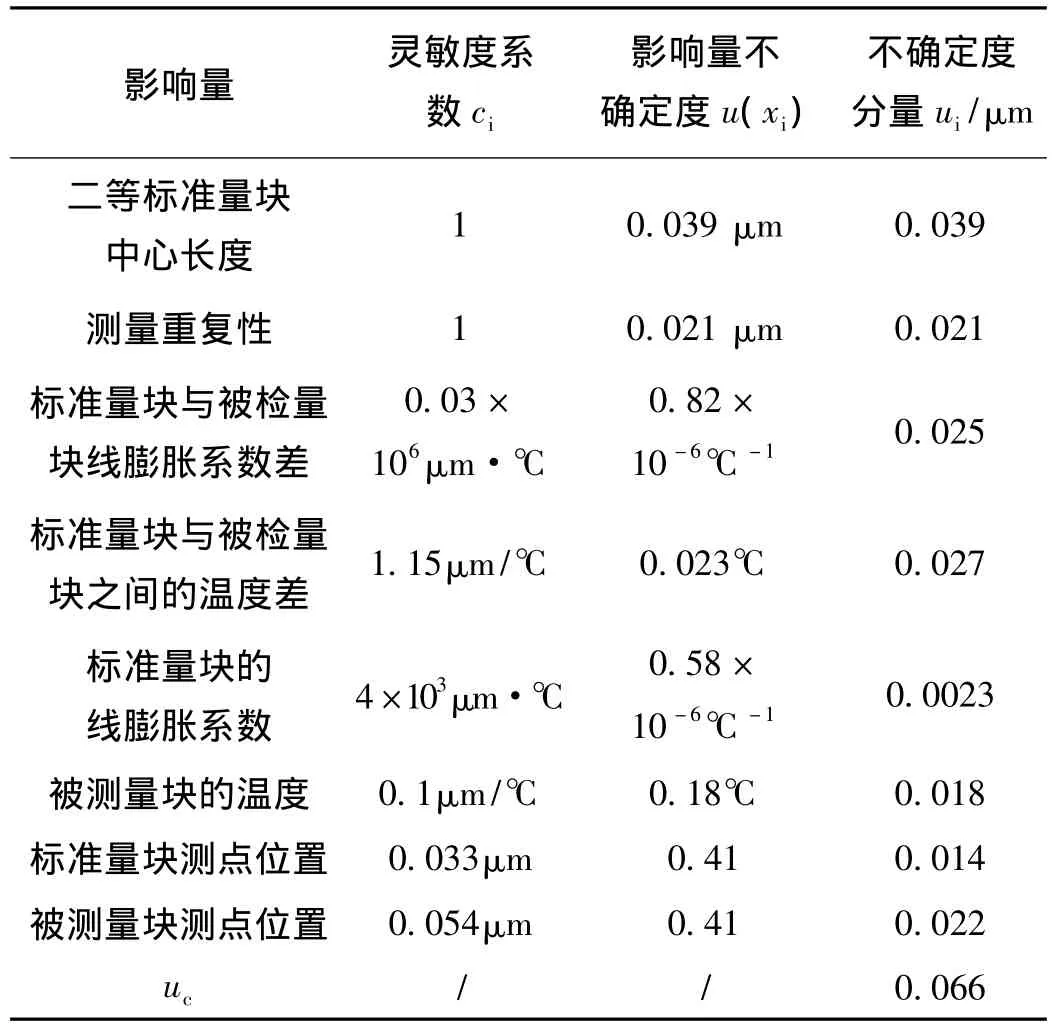
表1 測量不確定度分量明細表

取包含概率99%，得到以下結果:

被測量塊標稱長度為:100 mm；量塊中心長度偏差:-0.58μm；標準偏差為:0.07μm；包含概率為:99%；包含區間為 ［-0.75μm，-0.41μm］。

1.4 采用自適應MCM法對量塊測量不確定度進行評定

采用MCM法評定不確定度時需合理選擇試驗次數即樣本量的大小M，也就是測量模型計算的次數。由于無法保證這個數是否足夠，因此可使用自適應方法選擇M。在執行自適應MCM的基本過程中，試驗次數不斷增加，直至所需要的各種結果達到統計意義上的穩定。如果某結果的兩倍標準偏差小于標準不確定度的數值容差時，則認定該數值結果穩定。

1.4.1 設定輸入量的概率密度函數

測量的數學模型采用公式 (4），被測量塊的中心長度依賴于8個相互獨立的輸入量，各輸入量的概率密度函數設定如下:

1 ）標準量塊長度ls

100 mm二等量塊的測量不確定度為0.039μm。根據證書，100mm標準量塊的中心長度偏差e為-0.18μm，則為標準量塊中心長度偏差設定正態分布N(e，(U/k）2），即N(-0.18，0.0392）。

2 ）電腦量塊比較儀測量標準與被測量塊長度差d

測得被測量塊與標準量塊中心長度差算術平均值為-0.40μm，計算實驗標準偏差為0.021μm。為d設定正態分布N(-0.40，0.0212）。

3 ）標準量塊線膨脹系數αs

鋼質量塊的線膨脹系數在 (11.5±1） ×10-6℃-1范圍內，下限為 10.5×10-6℃-1，上限為 12.5×10-6℃-1。為αs設定矩形分布R(10.5×10-6，12.5 ×10-6）。

4 ）被檢量塊與標準量塊膨脹系數差Δα

鋼制量塊膨脹系數為 (11.5±1）×10-6℃-1，假定標準量塊和被測量塊的線膨脹系數均在±1×10-6℃-1的范圍內等概率分布，則兩量塊的線膨脹系數差應在±2×10-6℃-1范圍內，并服從三角分布。為Δα設定三角分布T(9.5×10-6，13.5×10-6）。

5 ）被測量塊溫度t

量塊比較測量時一般均不測量被測量塊的溫度t，即認為溫度等于20℃。因此被測量塊的溫度與20℃的差就是其不確定度范圍。下限為19.7℃，上限為20.3℃，為t設定矩形分布R(19.7，20.3）。

6 ）被測量塊與標準量塊溫度差Δt

檢定三等量塊時溫度最大差在±0.04℃范圍內估計，下限為-0.04℃，上限為0.04℃，為Δt設定矩形分布R(-0.04，0.04）。

7 ）標準量塊長度變動量δs(ΔPs）

100 mm二等量塊長度變動量允許值是0.12μm，估計測點位置在量塊中心附近1 mm區域內，則δs(ΔPs）下限為 -0.033 μm，上限為 0.033 μm，為δs(ΔPs）設定三角分布T(-0.033，0.033）。

8 ）被測量塊長度變動量δ(ΔP）

100 mm二等量塊長度變動量允許值是0.20μm，估計測點位置在量塊中心附近1 mm區域內，則δ(ΔP）下限為-0.054μm，上限為0.054μm，即為δ(ΔP）設定三角分布T(-0.054，0.054）。

1.4.2 自適應法運算程序

1.4.3 運算結果

MATLAB程序運行結果如下:

蒙特卡洛試驗次數為 540000；被測量塊標稱長度為100 mm；量塊中心長度偏差為-0.58μm；標準偏差為0.06μm；包含概率為99%；包含區間為 ［-0.74 μm，-0.43μm］。圖1給出了上述程序運行得到的輸出量頻次分布。

圖1 輸出量頻次分布圖

2 結論

采用MCM與GUM對量塊測量不確定度的評定結果進行比較，比較結果列入表2中。

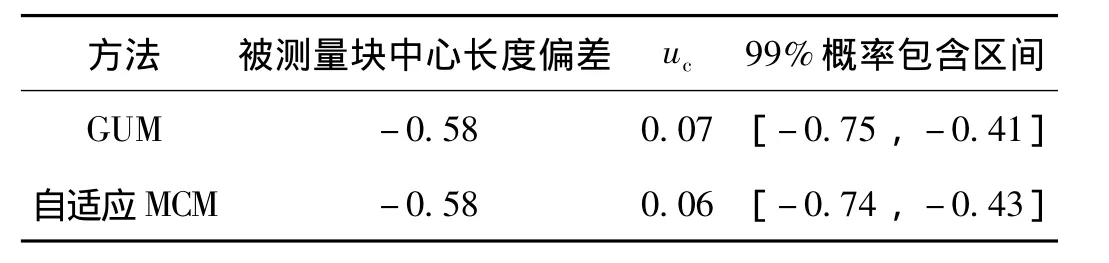
表2 量塊測量不確定度評定結果 μm

比較可見，在量塊中心長度的不確定度評定中，兩種方法得到的標準不確定度基本一致，GUM得到的包含區間略微保守。量塊規程中規定100 mm三等量塊的測量不確定度為0.20 mm，兩種方法均滿足要求。因此，在日常測量中，我們可以繼續延用GUM法對量塊測量不確定度進行評定。

［1］國家質量監督檢驗檢疫總局.JJF1059.2-2012用蒙特卡洛法評定測量不確定度［S］.北京:中國計量出版社，2012.

［2］ ISO/IEC.Evaluation of measurement data-Supplement 1 to the“Guide to the expression of uncertainty inmeasurement”-Propagation of distributions using a Monte Carlo method［S］.2008.

［3］國家質量監督檢驗檢疫總局.JJG146-2011量塊檢定規程［S］.北京:中國計量出版社，2011.

［4］陳懷艷，曹蕓，韓潔.基于蒙特卡羅法的測量不確定度評定［J］.電子測量與儀器學報，2011，25(4）:301-308.

［5］倪育才.實用測量不確定度評定 ［M］.北京:中國計量出版社，2010.