看圖學數理
曼尼斯·凱洛許

1、2、3、4、5……我們常用這些數字來數數。數的用途很多,比如用來做游戲。很多人發現:用不同的方法把數加在一起,可以創造出很多有趣的圖案。
你用數字能創造出哪些有趣的圖案呢?
表示數的方法很多。可以在紙上畫
在桌上放6張郵票,把它們排成一對一對的,最后一個也沒有剩。
把所有東西通通配成對,一個也沒剩,我們就說它是偶數。所以6就是偶數。
有時候,老師會要求班上的同學兩個兩個排一排。如果每個同學都能找到伴,配成對,那么班上的人數就是偶數。如果其他人都配成對后,還剩一個同學沒找到伴,配不成對,那么班上的人數就是奇數。
在桌上放5個蘋果,試著把它們兩兩配對。因為有一個配不成對,所以5是奇數。
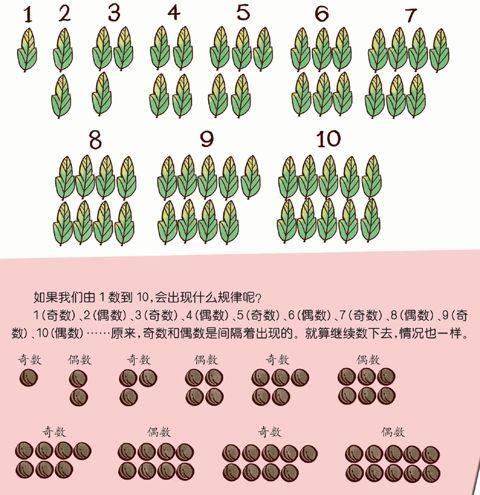
如果從1按順序寫到10,就叫“連續整數”。這些數當中,哪些是偶數呢?是不是2、4、6、8、10?有沒有看到下圖中這五個數下面的樹葉,都能兩兩配對?如果這五個數按由小到大或由大到小的順序寫下來,就叫做“連續偶數”。
同樣地,1、3、5、7、9這五個數下面的樹葉不能完全兩兩配對,最后都剩一片,這五個數就是奇數,按順序寫下來,就是“連續奇數”。
如果我們由1數到10,會出現什么規律呢?
1(奇數)、2(偶數)、3(奇數)、4(偶數)、5(奇數)、6(偶數)、7(奇數)、8(偶數)、9(奇數)、10(偶數)……原來,奇數和偶數是間隔著出現的。就算繼續數下去,情況也一樣。
那17是奇數還是偶數呢?你可以拿17個小球出來做實驗。把它們兩兩配對,看最后有沒有剩下一個。也可以在嘴里依次念“奇數—偶數—奇數……”的口訣,念一聲,就拿走一個小球,一直念到17,來檢驗剛才的答案對不對。
如果用不同的方法把這些數字相加,會得到什么數呢?
兩個偶數相加,會得奇數還是偶數呢?讓我們用下面的圖片加加看。
你不用算就知道,這些小車剛好兩兩配對,一個也不剩,所以結果是一個偶數。把兩個偶數加在一起,結果還是一個偶數。你發現了嗎?
偶數+偶數=偶數
按照數量,在桌上擺兩組珠子,然后把上圖右邊那組左右顛倒,變成下圖中的樣子。
把兩組珠子組合起來,原來每組各多出來的一個珠子,正好重新兩兩配對,最后可得到左圖的結果。
看到了嗎?隨便把兩個奇數兩兩相加,會得到一個偶數。
奇數+奇數=偶數
知道上面的規律后,不需配對,我們就可知道17是奇數:17=7+10=奇數+偶數=奇數。用這樣的方法就可方便地得出比10大的數是奇數還是偶數了。例如14=4+10=偶數+偶數=偶數。那么11、12、14、15、16、18、19是什么數呢?
你會發現:
一個兩位數,如果個位上的數是奇數,那么這個數就是奇數;如果個位上是偶數,那么它就是偶數。即使十位數字不是1,這個規律也成立。
除了配對以外,還能用其他圖案來表示奇數。下面是數字“7”的配對圖案。把下圖上排的3個扇貝換個方向,與下排的4個扇貝形成一個像書角一樣的新圖案。
用同樣的方法,把連續奇數排成下面的圖案。
從1開始的連續奇數相加,結果會是什么呢?1和3相加得4,相加以后的圖案是正方形,如右圖所示,所以說4是“平方數”。在4的正方形圖案中,每邊都有2個紐扣。所以,我們說4是2的平方,2的平方是4。
左面的圖案雖然是正方形,但它的數目不是平方數。平方數圖案的每一排一定有一樣多的紐扣。
讓我們在1和3相加的基礎上再加上下一個奇數5。我們又得到了一個正方形的圖案,它是平方數。這個平方數每邊都有3個紐扣。所以,9是3的平方,3的平方是9。
用同樣的方法加上下一個奇數7看看。是不是又排成一個正方形呢?它是不是平方數?
再想想看,1是不是平方數?它是不是每邊都只有一個東西的正方形?因此,1是1的平方,1的平方是1。
從1開始的連續奇數相加,可以排成一個正方形的圖案,也就是說,它們加起來是平方數。
例如1+3+5+7=16,我們可以看出,16排成了一個正方形的圖案,它是平方數,每邊有4個紐扣。所以,16是4的平方,4的平方是16。
你能證明下一個平方數是25嗎?以此類推,你又能證明接下來的三個平方數分別是36、49、64嗎?如果東西不夠擺,可以在紙上畫圓圈或黑點來代替。
趕緊動手試試吧!

