坡度對(duì)長(zhǎng)大坡道橋上無(wú)縫道岔的影響分析

顏 樂(lè)，熊震威，魏賢奎，王 平

(西南交通大學(xué)高速鐵路線路工程教育部重點(diǎn)實(shí)驗(yàn)室，成都 610031)

隨著既有繁忙干線大范圍換鋪跨區(qū)間無(wú)縫線路以及新線全面推廣一次鋪設(shè)跨區(qū)間無(wú)縫線路，我國(guó)在橋上無(wú)縫線路、路基上無(wú)縫道岔等方面的技術(shù)日漸成熟。無(wú)縫道岔作為跨區(qū)間無(wú)縫線路的關(guān)鍵技術(shù)［1］，近年來(lái)到得了迅猛發(fā)展，理論和實(shí)踐經(jīng)驗(yàn)已經(jīng)比較成熟。但是由于環(huán)保、節(jié)約用地或者地形條件的限制，將會(huì)有越來(lái)越多的無(wú)縫道岔鋪設(shè)在橋梁上［2］。在山區(qū)鐵路的困難地段，其特點(diǎn)之一是線路坡度大［3-4］，列車在山區(qū)地段的長(zhǎng)大坡道運(yùn)行時(shí)經(jīng)常需要制動(dòng)，而且其制動(dòng)比在平原地帶更為復(fù)雜。尚未有學(xué)者從橋上無(wú)縫道岔制動(dòng)這一角度出發(fā)，研究坡度對(duì)制動(dòng)工況下梁軌相互作用的影響。為了完善橋上無(wú)縫道岔計(jì)算理論，正確指導(dǎo)橋上無(wú)縫道岔的鋪設(shè)，很有必要研究坡度對(duì)長(zhǎng)大坡道橋上無(wú)縫道岔制動(dòng)工況的影響。

本文以某新建鐵路大橋?yàn)槔錁蛏蠠o(wú)縫道岔鋪設(shè)于17.2‰的大坡道上，在國(guó)內(nèi)是首例，而我國(guó)橋上無(wú)縫道岔鋪設(shè)地段的坡度一般不大于6‰［5］，為保證列車運(yùn)行的安全和穩(wěn)定性，需要重點(diǎn)關(guān)注列車制動(dòng)所引起的梁軌相互作用［6］，對(duì)其鋪設(shè)方案可行性進(jìn)行研究。本文考慮了 0‰、3‰、6‰、9‰、12‰、15‰、18‰、20‰八種不同的坡度，研究列車制動(dòng)情況下坡度對(duì)橋上無(wú)縫道岔受力變形的影響，對(duì)長(zhǎng)大坡道上鋪設(shè)橋上無(wú)縫道岔提出建議。

1 計(jì)算模型

1.1 道岔－橋梁相互作用原理

道岔－橋梁相互作用原理是橋上無(wú)縫道岔縱向力和位移計(jì)算的理論基礎(chǔ)。道岔里軌發(fā)生伸縮位移后，帶動(dòng)岔枕縱向移動(dòng)和偏轉(zhuǎn)，一部分作用力通過(guò)扣件傳遞給基本軌，一部分作用力通過(guò)岔枕傳遞給道床再傳遞給橋梁。橋梁因伸縮或撓曲在梁面上產(chǎn)生縱向位移，墩臺(tái)因道岔上傳下來(lái)的力在墩頂產(chǎn)生縱向位移，并帶動(dòng)橋梁產(chǎn)生縱向位移。同時(shí)，梁的位移通過(guò)道床傳到道岔上，會(huì)導(dǎo)致鋼軌中的縱向力重新分布，進(jìn)而再影響橋梁的受力與變形。可見(jiàn)，鋼軌、岔枕、橋梁及墩臺(tái)是一個(gè)相互作用、相互影響的耦合系統(tǒng)［7］，只有建立一體化模型，才能弄清道岔及橋梁的受力變形規(guī)律。

1.2 計(jì)算模型及單元選取

從整個(gè)線橋系統(tǒng)出發(fā)，將道岔和橋梁作為一個(gè)相互作用、相互影響的耦合系統(tǒng)，基于非線性有限單元法建立了岔-橋-墩一體化模型［8］。此模型考慮了影響縱向力分布的2個(gè)重要因素:線路縱向阻力及橋梁下部結(jié)構(gòu)的縱向水平剛度，如圖1所示。

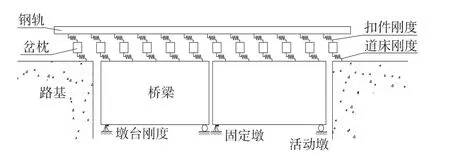
圖1 橋上有砟無(wú)縫道岔模型立面

對(duì)岔-橋-墩一體化模型采用桿單元模擬鋼軌和橋梁，采用梁?jiǎn)卧M道岔板和道床板。扣件縱向阻力、道岔板與底座板縱向阻力、滑動(dòng)層摩擦阻力、摩擦板縱向阻力、道岔傳力部件阻力、有砟軌道道床阻力等均采用非線性彈簧模擬。底座板上縱橫向凸臺(tái)、底座板與橋梁間的剪力齒槽、端刺和墩臺(tái)均采用線性彈簧模擬，線性彈簧的剛度依據(jù)各自受力與變形關(guān)系確定。這樣整個(gè)系統(tǒng)就可以采用桿單元、梁?jiǎn)卧⒕€性彈簧單元和非線性彈簧單元4種類型的單元來(lái)模擬。

1.3 計(jì)算參數(shù)

某新建鐵路大橋?yàn)?3 m簡(jiǎn)支梁+(32.4+33+32.4+33+32.4+33)m連續(xù)梁+(48.6+79.8+48.6)連續(xù)梁+32.4 m簡(jiǎn)支梁+16.2 m簡(jiǎn)支梁+16.8 m簡(jiǎn)支梁橋，道岔為單渡線18號(hào)無(wú)縫道岔，鋪設(shè)于17.2‰的大坡道上，道岔與橋梁布置如圖2所示。新建鐵路采用雙線有砟軌道，大橋從左到右、從下到上將2組道岔編號(hào)，1、2號(hào)道岔岔心里程分別為DK128+45.332、DK127+962.552，線間距為4.6 m。道床阻力參數(shù)及其他相關(guān)設(shè)計(jì)參數(shù)根據(jù)《新建鐵路橋上無(wú)縫線路設(shè)計(jì)暫行規(guī)定》(鐵建設(shè)函［2003］205號(hào))取值。列車荷載采用我國(guó)高速鐵路活載圖式(ZK活載)換算為均布荷載。

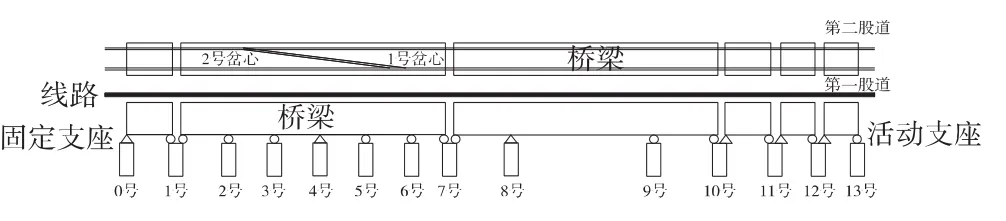
圖2 橋梁墩臺(tái)與道岔布置簡(jiǎn)圖

1.4 等效輪軌黏著系數(shù)

制動(dòng)力是通過(guò)輪軌摩擦直接作用于軌面，然后通過(guò)扣件或道砟將部分荷載傳遞到橋梁墩臺(tái)［9］。作用于軌面的制動(dòng)力集度q=μ·Q。μ為輪軌黏著系數(shù)，“八五”國(guó)家科技攻關(guān)項(xiàng)目《高速鐵路線橋隧設(shè)計(jì)參數(shù)選擇的研究》之報(bào)告三《高速鐵路軌道理論計(jì)算模式與參數(shù)建議值》中建議輪軌黏著系數(shù)取0.164，根據(jù)我國(guó)多年的試驗(yàn)研究和工程實(shí)踐，輪軌黏著系數(shù)采用0.164是合適的［10］;Q為設(shè)計(jì)荷載。

由于該道岔梁位于坡道上，制動(dòng)荷載還應(yīng)疊加上ZK活載的坡道分力。在計(jì)算中通過(guò)將坡道上的制動(dòng)荷載轉(zhuǎn)化為等效輪軌黏著系數(shù)μ0實(shí)現(xiàn)。在圖3中，設(shè)計(jì)荷載為Q，平行于軌道的分力F2即為坡道分力［11］

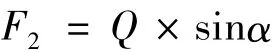
因?yàn)棣两且话愫苄。闪顂inα≈tanα，于是

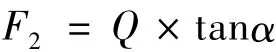
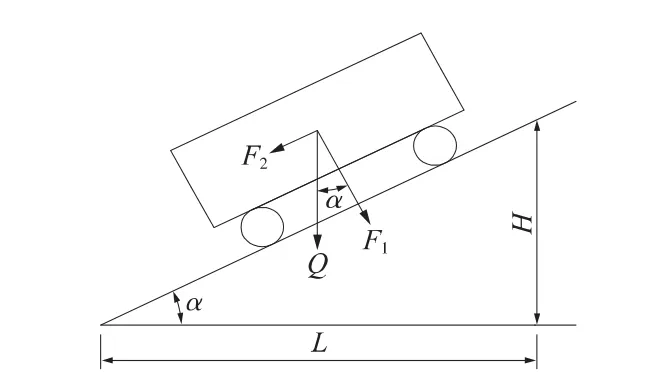
圖3 坡道分力示意

線路坡度 i=H/L=tanα，故

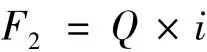
因此，長(zhǎng)大坡道上的等效輪軌黏著系數(shù)為μ0=μ+i，即μ0=0.164+i，作用于軌面的制動(dòng)力集度q=μ0·Q。

1.5 計(jì)算工況

由于列車左入橋與右入橋2種工況下的梁軌相互作用規(guī)律基本相同，因此只分析從右向左入橋的情況，采用一線制動(dòng)，分別考慮圖4中幾種制動(dòng)工況。

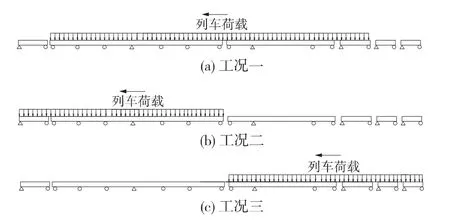
圖4 制動(dòng)工況

經(jīng)計(jì)算比較，無(wú)論是鋼軌力還是位移，工況一都最大，因此取工況一進(jìn)行坡度對(duì)橋上無(wú)縫道岔制動(dòng)工況的影響分析，不同的坡度如表1所示。

表1 不同坡度計(jì)算工況

2 計(jì)算結(jié)果及分析

2.1 坡度對(duì)鋼軌縱向力的影響

坡度分別為 0‰、3‰、6‰、9‰、12‰、15‰、18‰、20‰時(shí)，最大鋼軌縱向拉、壓力變化如圖5所示。

從圖5中可以看出，隨著坡度的增大，鋼軌的最大縱向拉、壓力均近似呈線性遞增。20‰坡度的最大鋼軌縱向拉力比0‰的增加了12.21%，最大鋼軌縱向壓力也增加了12.19%。

2.2 坡度對(duì)位移的影響

坡度分別為 0‰、3‰、6‰、9‰、12‰、15‰、18‰、20‰時(shí)，梁軌相對(duì)位移最大值變化、鋼軌最大位移變化如圖6所示。

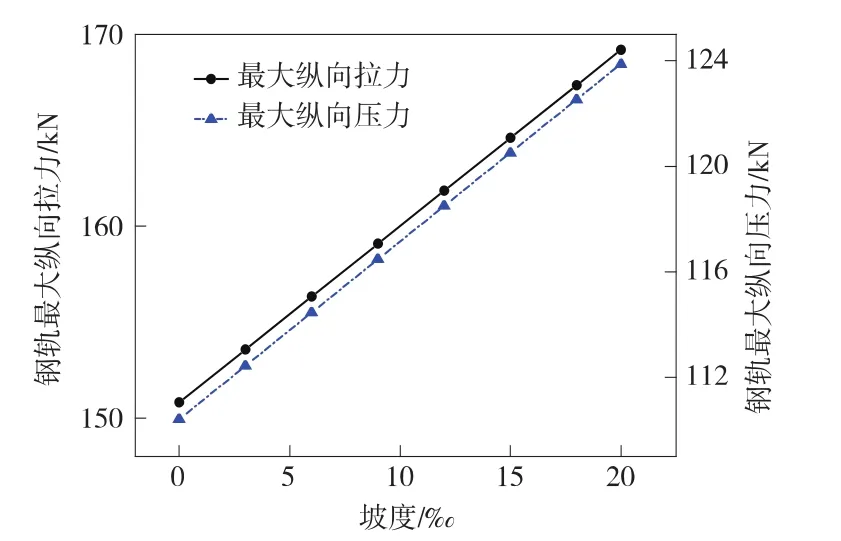
圖5 鋼軌最大縱向拉力和壓力

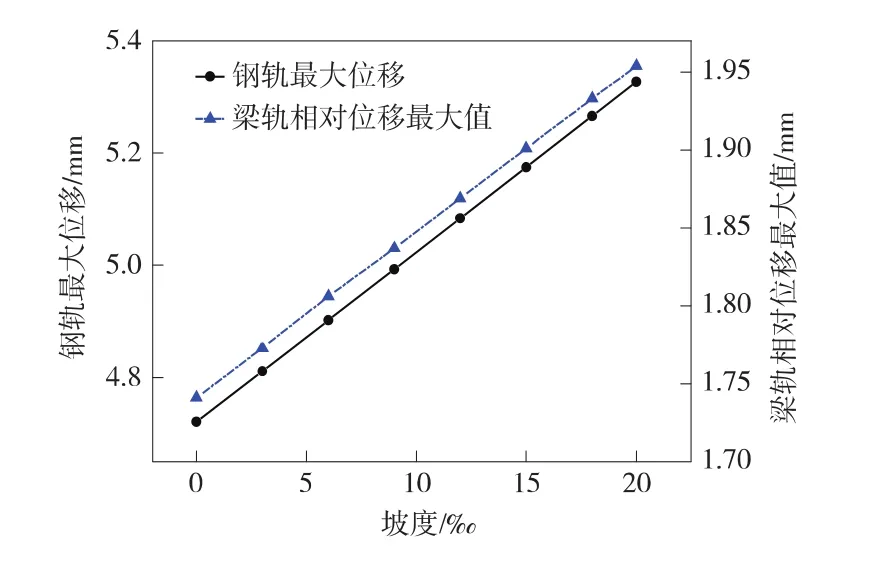
圖6 梁軌相對(duì)位移最大值和鋼軌最大位移

從圖6中可以看出，隨著坡度的增大，梁軌相對(duì)位移、鋼軌最大位移都近似呈線性遞增。20‰坡度的梁軌相對(duì)位移最大值比0‰的增加了12.23%，鋼軌最大位移也增加了12.84%。

2.3 坡度對(duì)墩臺(tái)縱向力的影響

坡度分別為 0‰、3‰、6‰、9‰、12‰、15‰、18‰、20‰時(shí)，各固定墩臺(tái)的縱向力如表2所示。

表2 不同坡度時(shí)的墩臺(tái)縱向力 kN

選取4號(hào)和8號(hào)墩臺(tái)(固定支座)做比較，其墩臺(tái)縱向力變化如圖7所示。

從圖7中可以看出，隨著坡度的增大，墩臺(tái)縱向力絕對(duì)值近似呈線性遞增。對(duì)4號(hào)墩臺(tái)，20‰坡度的墩臺(tái)縱向力比0‰的增加了12.18%。對(duì)8號(hào)墩臺(tái)，20‰坡度的墩臺(tái)縱向力比0‰的增加了12.21%。

2.4 其他計(jì)算結(jié)果

取1號(hào)道岔作為比較，道岔傳力部件的位移和縱向力見(jiàn)表3(注:由于同組道岔直、曲尖軌位移相差較小且通常曲尖軌位移稍大，表3中尖軌位移取曲尖軌位移;由于限位器不受縱向力，因此只列舉了直、側(cè)股間隔鐵的受力)。

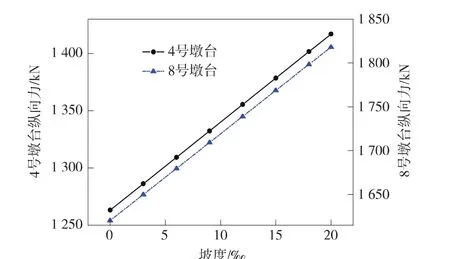
圖7 4號(hào)和8號(hào)墩臺(tái)縱向力

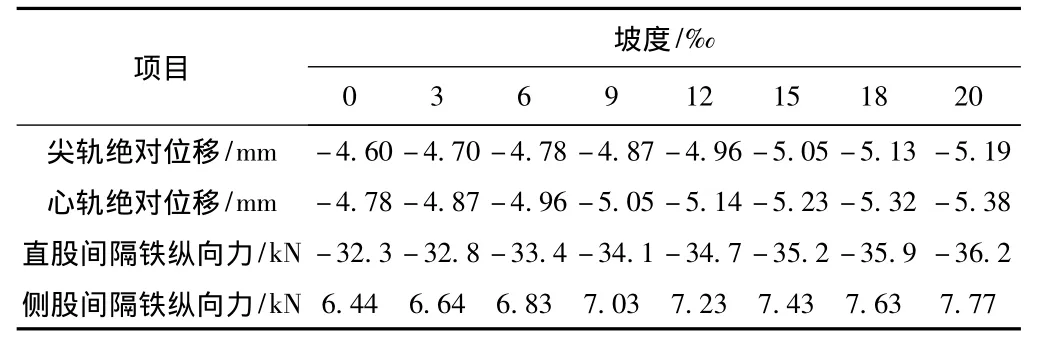
表3 計(jì)算結(jié)果比較

心軌、尖軌尖端絕對(duì)位移、直側(cè)股間隔鐵縱向力隨坡度變化如圖8、圖9所示。

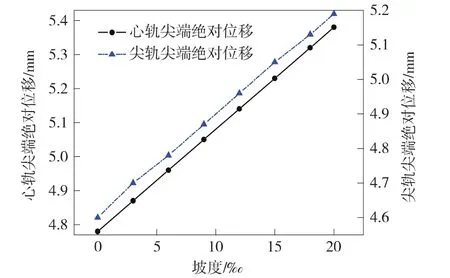
圖8 心軌、尖軌尖端絕對(duì)位移

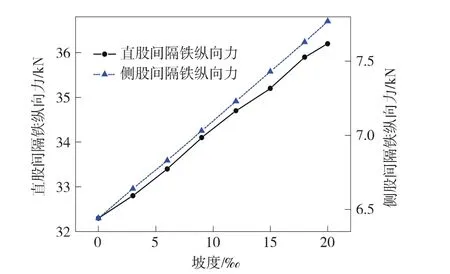
圖9 直股、側(cè)股間隔鐵縱向力

從表3和圖8、圖9可以看出，隨著坡度的增大，心軌和尖軌的絕對(duì)位移以及間隔鐵的縱向力都近似呈線性遞增。其中，20‰坡度尖軌尖端的絕對(duì)位移比0‰的增加了12.83%，20‰坡度心軌尖端的絕對(duì)位移比0‰的增加了12.55%，20‰坡度的直股間隔鐵縱向力比0‰的增加了12.07%，20‰坡度的側(cè)股間隔鐵縱向力比0‰的增加了20.6%。

由圖9還可以看出，側(cè)股間隔鐵的縱向力比直股間隔鐵小，但是其受坡度的影響卻較大。這主要是由于制動(dòng)是一線(正線)制動(dòng)，直股間隔鐵承受正線上的長(zhǎng)心軌傳遞來(lái)的縱向力，側(cè)股間隔鐵承受側(cè)線上的短心軌傳遞的縱向力，因此直股間隔鐵的縱向力比較大;長(zhǎng)大坡道制動(dòng)時(shí)，側(cè)股間隔鐵承受正線上的導(dǎo)軌傳遞的縱向力，而直股間隔鐵承受側(cè)線上的導(dǎo)軌傳遞的縱向力，因此側(cè)股間隔鐵受坡度的影響較大。

3 結(jié)論

通過(guò)建立有砟軌道岔-橋-墩一體化模型，分析了列車制動(dòng)情況時(shí)，坡度對(duì)橋上無(wú)縫道岔受力與變形的影響，對(duì)長(zhǎng)大坡道上無(wú)縫道岔的鋪設(shè)進(jìn)行了思考和總結(jié)，結(jié)論如下。

(1)隨著坡度的增大，鋼軌縱向力、鋼軌位移、墩臺(tái)縱向力、心軌和尖軌位移以及間隔鐵縱向力都近似呈線性遞增。因此，坡度的增大對(duì)無(wú)縫道岔的受力和變形都是不利的。

(2)側(cè)股間隔鐵的縱向力比直股間隔鐵小，但是其受坡度的影響卻較大。

(3)由于長(zhǎng)軌條在長(zhǎng)大坡道容易產(chǎn)生不均勻的爬行現(xiàn)象，而這種爬行又會(huì)受到道岔的阻礙作用，便導(dǎo)致道岔的受力變形規(guī)律更加復(fù)雜［12］。在鐵路現(xiàn)場(chǎng)，應(yīng)加強(qiáng)無(wú)縫道岔防爬鎖定，并加密防爬觀測(cè)次數(shù)。

因此，橋上無(wú)縫道岔的坡度限值有待進(jìn)一步研究確定。

［1］王平，劉學(xué)毅.無(wú)縫道岔計(jì)算理論與設(shè)計(jì)方法［M］.成都:西南交通大學(xué)出版社，2007:1-2.

［2］王平，楊榮山，劉學(xué)毅.無(wú)縫道岔鋪設(shè)于長(zhǎng)大連續(xù)梁橋上時(shí)的受力與變形分析［J］.交通運(yùn)輸工程與信息學(xué)報(bào)，2004，2(3):16-21.

［3］高亮亮，龔愛(ài)軍.山區(qū)鐵路改河工程設(shè)計(jì)方案研究［J］.鐵道標(biāo)準(zhǔn)設(shè)計(jì)，2012(11):72-74.

［4］文沛溪.在15‰大坡道上無(wú)縫線路的爬行觀察及其分析［J］.鐵道標(biāo)準(zhǔn)設(shè)計(jì)通訊，1977(5):33-37.

［5］王平，陳嶸，楊榮山，劉學(xué)毅.橋上無(wú)縫道岔設(shè)計(jì)理論［M］.成都:西南交通大學(xué)出版社，2011:20-23.

［6］曲村，高亮，侯博文.城市軌道交通長(zhǎng)大橋梁上無(wú)縫線路鋼軌制動(dòng)力研究［J］.城市軌道交通研究，2012(10):66-70.

［7］楊榮山.橋上無(wú)縫道岔縱向力計(jì)算理論與試驗(yàn)研究［D］.成都:西南交通大學(xué)土木工程學(xué)院，2008.

［8］李秋義.客運(yùn)專線橋上無(wú)縫道岔計(jì)算模型和計(jì)算方法研究［J］.鐵道標(biāo)準(zhǔn)設(shè)計(jì)，2010(2):64-66.

［9］雷俊卿，李宏年，馮東.鐵路橋梁列車制動(dòng)力的試驗(yàn)研究與計(jì)算分析［J］.工程力學(xué)，2006(3):134-140.

［10］中華人民共和國(guó)鐵道部.鐵建設(shè)函［2003］205號(hào) 新建鐵路橋上無(wú)縫線路設(shè)計(jì)暫行規(guī)定［S］.北京:中國(guó)鐵道出版社，2003.

［11］易思蓉.鐵路選線設(shè)計(jì)［M］.成都:西南交通大學(xué)，2009:57-58.

［12］王平，郭利康.線路爬行對(duì)無(wú)縫道岔受力與變形的影響分析［J］.西南交通大學(xué)學(xué)報(bào)，2002(12):615-619.