基于隨機(jī)模擬技術(shù)的地震風(fēng)險(xiǎn)評(píng)估與損失分擔(dān)機(jī)制設(shè)計(jì)

田玲 姚鵬

(武漢大學(xué)經(jīng)濟(jì)與管理學(xué)院，湖北 武漢 430072)

我國(guó)是世界上遭受巨災(zāi)影響最為嚴(yán)重的國(guó)家之一。僅在2008年，南方雪災(zāi)、汶川地震以及南方諸省的暴雨洪災(zāi)相繼爆發(fā)，各類自然災(zāi)害共造成約4.7億人(次)受災(zāi)，死亡和失蹤88928人，緊急轉(zhuǎn)移安置2682.2萬(wàn)人(次);農(nóng)作物受災(zāi)面積3999萬(wàn) hm2，絕收面積403.2萬(wàn) hm2;倒塌房屋1097.7萬(wàn)間;因?yàn)?zāi)直接經(jīng)濟(jì)損失13547.5億元。而近期發(fā)生的北京“721”特大自然災(zāi)害、云南昭通泥石流更是令全國(guó)唏噓不已。

目前，我國(guó)并不具備一套健全的巨災(zāi)風(fēng)險(xiǎn)損失分擔(dān)機(jī)制，在歷次巨災(zāi)發(fā)生后，政府依然是沖到了賠償與救助的“第一線”，保險(xiǎn)市場(chǎng)無(wú)所作為。縱觀當(dāng)今世界，不論是經(jīng)濟(jì)發(fā)達(dá)的美國(guó)和日本，抑或是處于發(fā)展中國(guó)家的土耳其，巨災(zāi)保險(xiǎn)制度在巨災(zāi)風(fēng)險(xiǎn)管理中發(fā)揮著舉足輕重的作用，其中的巨災(zāi)風(fēng)險(xiǎn)損失分擔(dān)機(jī)制功不可沒。

那么該如何設(shè)計(jì)適合我國(guó)的巨災(zāi)風(fēng)險(xiǎn)損失分擔(dān)機(jī)制呢?是否存在一種方法使得設(shè)計(jì)出的分擔(dān)機(jī)制能夠承擔(dān)巨災(zāi)風(fēng)險(xiǎn)的“小概率、大損失”呢?巨災(zāi)風(fēng)險(xiǎn)如果不僅僅是通過單一的保險(xiǎn)人和再保險(xiǎn)人進(jìn)行承保，而是更多的發(fā)揮社會(huì)各方面的力量，在以保險(xiǎn)為手段的前提下，使風(fēng)險(xiǎn)得以在各主體之間分擔(dān)，那么保險(xiǎn)在應(yīng)對(duì)巨災(zāi)風(fēng)險(xiǎn)時(shí)就會(huì)顯得游刃有余。基于此，本文主要以地震風(fēng)險(xiǎn)為研究對(duì)象，采用隨機(jī)模擬技術(shù)對(duì)我國(guó)的地震風(fēng)險(xiǎn)進(jìn)行評(píng)估，提出設(shè)計(jì)地震風(fēng)險(xiǎn)損失分擔(dān)機(jī)制的方法，并在一定假設(shè)的基礎(chǔ)上設(shè)計(jì)了我國(guó)地震風(fēng)險(xiǎn)損失分擔(dān)機(jī)制。

1 文獻(xiàn)回顧

近幾年，國(guó)內(nèi)學(xué)者開始了對(duì)巨災(zāi)風(fēng)險(xiǎn)損失分擔(dān)機(jī)制的探討。謝世清［1］認(rèn)為單純依靠市場(chǎng)手段構(gòu)建巨災(zāi)保險(xiǎn)制度具有公司承保能力有限導(dǎo)致的保險(xiǎn)費(fèi)率較高等弊端，但單純依靠政府的手段由于巨大的財(cái)政壓力依然無(wú)法解決問題。姚慶海［2］、卓志等［3］認(rèn)為，我國(guó)建立整體性的巨災(zāi)風(fēng)險(xiǎn)損失分擔(dān)機(jī)制需要政府和市場(chǎng)共同發(fā)揮作用，通過居民、巨災(zāi)保險(xiǎn)保障基金、保險(xiǎn)市場(chǎng)、再保險(xiǎn)市場(chǎng)和資本市場(chǎng)共同參與來(lái)完成。趙苑達(dá)［4］認(rèn)為應(yīng)當(dāng)將政府的災(zāi)害救助基金設(shè)為巨災(zāi)保險(xiǎn)保障基金，專款專用，逐年提取。充分發(fā)揮我國(guó)巨災(zāi)主體的風(fēng)險(xiǎn)分散作用，建立“多層次”的巨災(zāi)風(fēng)險(xiǎn)損失分擔(dān)機(jī)制。

國(guó)外學(xué)者對(duì)于巨災(zāi)風(fēng)險(xiǎn)損失分擔(dān)機(jī)制的研究已經(jīng)有很長(zhǎng)的時(shí)間。Cummins等［5］對(duì)美國(guó)財(cái)險(xiǎn)市場(chǎng)進(jìn)行了測(cè)算，結(jié)果顯示依據(jù)當(dāng)時(shí)的承保能力，美國(guó)財(cái)險(xiǎn)市場(chǎng)只能承擔(dān)100億美元的巨災(zāi)損失。Niehaus［6］認(rèn)為逆向選擇問題會(huì)削減巨災(zāi)保險(xiǎn)人的承保能力。Swiss Re［7］的研究表明，在PPP(Public-Private-Partnership，公私協(xié)作)模式下，再保險(xiǎn)公司可以設(shè)計(jì)依托政府與民間的巨災(zāi)再保險(xiǎn)，這樣既降低了再保險(xiǎn)費(fèi)率，擴(kuò)大了再保險(xiǎn)覆蓋率，又提高了社會(huì)整體應(yīng)對(duì)巨災(zāi)的能力。Cummins［8］認(rèn)為，通過巨災(zāi)債券，再保險(xiǎn)人可以提高自身的償付能力;作為政府，有必要采取相應(yīng)的手段防止自身累積過多的風(fēng)險(xiǎn)責(zé)任。Clarke［9］研究認(rèn)為，政府可以通過或有負(fù)債融資，減少作為風(fēng)險(xiǎn)分擔(dān)機(jī)制最后承擔(dān)者的風(fēng)險(xiǎn)。

通過國(guó)內(nèi)外研究現(xiàn)狀可以看出，學(xué)者一致認(rèn)為政府應(yīng)當(dāng)作為主要主體參與到巨災(zāi)風(fēng)險(xiǎn)損失分擔(dān)機(jī)制中，從而保證保險(xiǎn)人能夠發(fā)揮應(yīng)有的作用，個(gè)人、資本市場(chǎng)也應(yīng)該發(fā)揮相應(yīng)的作用。由于國(guó)外部分國(guó)家巨災(zāi)保險(xiǎn)制度已經(jīng)有相當(dāng)長(zhǎng)的歷史，其中的巨災(zāi)風(fēng)險(xiǎn)損失分擔(dān)機(jī)制不斷趨于成熟。因此，國(guó)外學(xué)者的研究較為深入，既探討了各個(gè)主體所面臨的困境，又提出了相應(yīng)的解決辦法。綜合目前國(guó)內(nèi)外的研究成果，尚有如下兩點(diǎn)需要改進(jìn):1)缺乏對(duì)于巨災(zāi)風(fēng)險(xiǎn)特點(diǎn)的把握，有些研究(Cummins等［5］)對(duì)于巨災(zāi)風(fēng)險(xiǎn)還是依賴于傳統(tǒng)的正態(tài)分布，無(wú)法體現(xiàn)巨災(zāi)的“小概率、大損失”特征;2)缺乏一個(gè)設(shè)計(jì)巨災(zāi)風(fēng)險(xiǎn)損失分擔(dān)機(jī)制科學(xué)合理的方法，不能從較為宏觀的角度劃分各個(gè)主體的分擔(dān)比例。

我國(guó)臺(tái)灣學(xué)者Chung-Hung Tsai［10］采用了隨機(jī)模擬技術(shù)對(duì)臺(tái)灣地區(qū)的旅游業(yè)進(jìn)行了風(fēng)險(xiǎn)評(píng)估，并在此基礎(chǔ)上對(duì)當(dāng)?shù)氐娘L(fēng)險(xiǎn)管理提出了建議。本文同樣應(yīng)用隨機(jī)模擬技術(shù)對(duì)我國(guó)大陸地區(qū)的地震風(fēng)險(xiǎn)進(jìn)行模擬，進(jìn)而對(duì)我國(guó)地震風(fēng)險(xiǎn)損失分擔(dān)機(jī)制的設(shè)計(jì)提出相應(yīng)的方法。但與Chung-Hung Tsai［10］的文章相比，本文有如下創(chuàng)新:1)對(duì)地震發(fā)生頻數(shù)的模擬不僅僅只是采用理論性較強(qiáng)的泊松分布，同樣考慮了負(fù)二項(xiàng)分布。而且通過模擬結(jié)果與現(xiàn)實(shí)數(shù)據(jù)對(duì)比發(fā)現(xiàn)，負(fù)二項(xiàng)分布的擬合效果更好，更能反映極端頻數(shù)。2)在對(duì)地震的損失評(píng)估方面，沒有直接采用歷次地震造成的損失金額，而是以地震震級(jí)代表地震風(fēng)險(xiǎn)損失的大小。這樣避免了由于歷次地震損失統(tǒng)計(jì)不全面以及由于物價(jià)與人口變動(dòng)產(chǎn)生的誤差。3)對(duì)地震震級(jí)發(fā)生的模擬采用了離散蒙特卡羅方法，較采用連續(xù)分布函數(shù)(如指數(shù)分布、帕累托分布)更為精確。4)與以往相關(guān)研究不同，本文采用超越概率曲線作為設(shè)計(jì)地震風(fēng)險(xiǎn)損失分擔(dān)機(jī)制的工具，將各個(gè)主體的分擔(dān)比例問題轉(zhuǎn)換為各個(gè)主體的風(fēng)險(xiǎn)容忍度問題。

2 研究方法

客觀世界的某些現(xiàn)象之間存在著某種相似性，因而可以通過歷史數(shù)據(jù)研究問題。在分析一個(gè)系統(tǒng)時(shí)，可以構(gòu)造一個(gè)與該系統(tǒng)相似的模型，通過在模型上進(jìn)行試驗(yàn)來(lái)研究原系統(tǒng)。隨機(jī)系統(tǒng)可以用概率模型描述并進(jìn)行試驗(yàn)，稱為隨機(jī)模擬方法。當(dāng)某一問題用傳統(tǒng)的方法計(jì)算較為復(fù)雜或有較大難度時(shí)，就可以采用隨機(jī)模擬方法。例如在分析保險(xiǎn)公司的資產(chǎn)與負(fù)債配比策略、聚合理賠風(fēng)險(xiǎn)等問題時(shí)，都可以用到隨機(jī)模擬方法［11］。具體到對(duì)我國(guó)地震風(fēng)險(xiǎn)的研究時(shí)，由于地震發(fā)生的復(fù)雜性與數(shù)據(jù)的稀缺性，采用隨機(jī)模擬技術(shù)研究地震風(fēng)險(xiǎn)較為適宜。

地震風(fēng)險(xiǎn)損失評(píng)估模型應(yīng)包括四個(gè)部分:地震頻數(shù)發(fā)生器;危險(xiǎn)性發(fā)生器;易損性分析;損失程度分析。各自之間的關(guān)系如下圖(圖1)所示:

圖1 地震風(fēng)險(xiǎn)隨機(jī)技術(shù)路線圖Fig.1 Technological process of earthquake risk stochastic simulation

首先，通過對(duì)地震發(fā)生頻數(shù)的歷史數(shù)據(jù)分析，選擇相應(yīng)的頻數(shù)分布模型，通常采用泊松分布模擬年度地震發(fā)生的頻數(shù)。通過頻數(shù)分布模型，模擬出N組頻數(shù)，每個(gè)頻數(shù)記作f(i)(i=1，...，N)。其次，由于歷史上不同震級(jí)的地震發(fā)生的頻率是不同的，而且不同震級(jí)所造成的損失差別較大，因此研究地震震級(jí)發(fā)生的經(jīng)驗(yàn)分布是及其重要的。通常來(lái)講，隨著震級(jí)的增加，其發(fā)生的概率遞減。根據(jù)震級(jí)的經(jīng)驗(yàn)分布函數(shù)，將震級(jí)分布擬合f(i)次，重復(fù)執(zhí)行N遍，得到N組震級(jí)頻數(shù)分布。再次，分別將N組地震震級(jí)分布中的地震震級(jí)加總，得到 mag(i)(i=1，2，...，N)。最后，通過mag(i)的分析，得到年度震級(jí)的超越概率曲線。

在年度震級(jí)超越概率曲線的基礎(chǔ)上，對(duì)各個(gè)主體風(fēng)險(xiǎn)承擔(dān)比例的劃分問題就轉(zhuǎn)化為了各個(gè)主體對(duì)于地震風(fēng)險(xiǎn)容忍度大小的問題。研究各個(gè)主體都能接受的風(fēng)險(xiǎn)容忍度是地震風(fēng)險(xiǎn)損失分擔(dān)機(jī)制的關(guān)鍵問題。

3 我國(guó)地震風(fēng)險(xiǎn)損失評(píng)估

本文對(duì)地震風(fēng)險(xiǎn)損失評(píng)估采用超越概率曲線的形式。損失曲線有兩種主要形式，一種是概率密度曲線，其函數(shù)表達(dá)式為f(x)=p(ε=x)，另一種是累計(jì)頻率曲線，其分為向上累積和向下累積，如果以概率的形式來(lái)表達(dá)，其函數(shù)形式分別為F1(x)=p(ε≥x)，F(xiàn)2(x)=p(ε≤x)。向下累積頻率分別可作為概率分布函數(shù)的估計(jì)，而向上累積曲線也就是通常所說(shuō)的超越概率曲線的估計(jì)。用超越概率曲線描述諸如地震等巨災(zāi)風(fēng)險(xiǎn)更為直觀，巨災(zāi)風(fēng)險(xiǎn)損失超過某一特定值的概率能通過坐標(biāo)軸形象的反映出來(lái)。單調(diào)遞減的函數(shù)性質(zhì)說(shuō)明隨著損失程度的增加，超過該損失的概率遞減。我國(guó)地震風(fēng)險(xiǎn)損失的超越概率曲線需要按照上文講到的步驟進(jìn)行繪制。本文假設(shè)地震震級(jí)與地震造成的經(jīng)濟(jì)損失呈正比例關(guān)系，所以此處用地震震級(jí)代表地震風(fēng)險(xiǎn)損失。

3.1 地震頻數(shù)發(fā)生器

就中國(guó)而言，每年地震發(fā)生的頻數(shù)差別較大，少則幾十次，多則幾百次。根據(jù)國(guó)務(wù)院辦公廳應(yīng)急管理辦公室制定的《國(guó)家地震應(yīng)急預(yù)案》中的地震災(zāi)害事件的分級(jí)標(biāo)準(zhǔn)規(guī)定，5級(jí)以上的地震就會(huì)導(dǎo)致一定的人員傷亡和經(jīng)濟(jì)損失，因此，本文所采用的歷史數(shù)據(jù)均為5級(jí)以上地震發(fā)生的頻數(shù)。圖2為中國(guó)自1910年開始每年發(fā)生的震級(jí)在5級(jí)以上地震的頻數(shù)時(shí)間序列圖。由圖可以看出，5級(jí)以上地震發(fā)生的頻數(shù)沒有明顯的周期性，大部分頻數(shù)都在40上下波動(dòng)，而且高頻數(shù)(100次以上)的地震難以預(yù)測(cè)，具有明顯的隨機(jī)性。

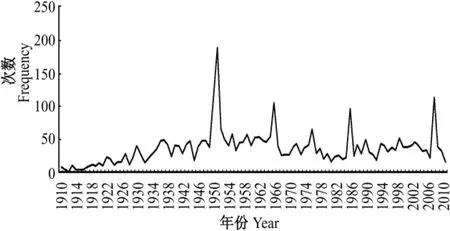
圖2 我國(guó)地震頻數(shù)時(shí)序圖Fig.2 Time series of earthquake frequency

地震頻數(shù)的時(shí)序描述性統(tǒng)計(jì)量如表1所示。通過統(tǒng)計(jì)量可以看出地震頻數(shù)的均值為37.3431，遠(yuǎn)遠(yuǎn)小于方差。如果只是采用泊松分布擬合會(huì)過于保守，無(wú)法突出高頻數(shù)的年度地震事件。負(fù)二項(xiàng)分布是統(tǒng)計(jì)上的一種離散分布，能反應(yīng)極端事件的發(fā)生。本文則分別采用泊松分布與負(fù)二項(xiàng)分布對(duì)地震頻數(shù)進(jìn)行模擬。各分布函數(shù)的形式見表2。

由表1與表2，可以得出泊松分布的估計(jì)參數(shù)為:λ^=37.3431，負(fù)二項(xiàng)分布的估計(jì)參數(shù)為:p^=0.055，r^=2.1734。分別采用隨機(jī)模擬技術(shù)，產(chǎn)生10000組數(shù)據(jù)，得到的頻率圖(圖3、4)如下。

表1 地震頻數(shù)描述性統(tǒng)計(jì)量Tab.1 Descriptive statistics of earthquack frequency

表2 泊松分布和負(fù)二次項(xiàng)Tab.2 Poisson distribution and negative binomial distribution

圖3 泊松分布模擬結(jié)果Fig.3 Result of poisson distribution stochastic simulation

對(duì)比實(shí)際地震頻數(shù)分布的頻率圖(圖5)，可以發(fā)現(xiàn)，負(fù)二項(xiàng)分布的模擬效果要好一些。通過圖5可以看出，負(fù)二項(xiàng)分布對(duì)于高頻數(shù)的結(jié)果均有所涉及。

3.2 地震震級(jí)發(fā)生器

圖4 負(fù)二項(xiàng)分布模擬結(jié)果Fig.4 Result of negative binomial distribution stochastic simulation

圖5 我國(guó)地震歷史頻數(shù)分布Fig.5 Historical frequency of earthquake in China

圖6 地震震級(jí)頻率直方圖Fig.6 Histogram of earthquake magnitude

圖7 地震震級(jí)經(jīng)驗(yàn)分布Fig.7 Empirical distribution function of earthquake magnitude

圖8 地震震級(jí)模擬結(jié)果Fig.8 Result of magnitude stochastic simulation

通過歷史數(shù)據(jù)來(lái)看，不同震級(jí)發(fā)生的頻率是不一樣的，一般而言，隨著震級(jí)的增加，發(fā)生的概率遞減。圖6表明1910年后不同震級(jí)發(fā)生的頻率直方圖，可以看出雖然地震級(jí)數(shù)與級(jí)數(shù)之間遞減關(guān)系不明顯，但是總體趨勢(shì)還是呈遞減狀。一般對(duì)于地震震級(jí)都采用指數(shù)分布進(jìn)行模擬，但是通過圖可以看出，地震震級(jí)的總體趨勢(shì)雖然遞減，但地震震級(jí)之間還是呈現(xiàn)高低交錯(cuò)的形態(tài)。本文采用以地震震級(jí)的歷史數(shù)據(jù)構(gòu)造地震震級(jí)的經(jīng)驗(yàn)分布函數(shù)。圖7是地震震級(jí)的經(jīng)驗(yàn)分布函數(shù)圖，圖8是基于地震震級(jí)的經(jīng)驗(yàn)分布函數(shù)模擬10000次的結(jié)果，可以看出，模擬結(jié)果與歷史頻率基本一致。

3.3 年度地震累積震級(jí)分布

第一部分采用泊松分布與負(fù)二項(xiàng)分布對(duì)年度地震的頻數(shù)進(jìn)行模擬，結(jié)果顯示負(fù)二項(xiàng)分布的模擬效果更能反映部分極端地震頻數(shù)，而泊松分布模擬結(jié)果顯得較為保守，具有一定的普遍性。第二部分通過地震震級(jí)的經(jīng)驗(yàn)分布函數(shù)采用隨機(jī)模擬技術(shù)對(duì)地震震級(jí)的發(fā)生進(jìn)行模擬，最終模擬的頻數(shù)結(jié)果與實(shí)際結(jié)果基本一致。本部分將上兩部分的結(jié)果相結(jié)合，模擬地震風(fēng)險(xiǎn)的年度震級(jí)累積和。

本文假設(shè)地震所造成的經(jīng)濟(jì)損失與地震震級(jí)成正比例的關(guān)系［13］，即:

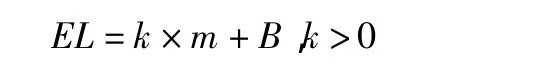
其中，EL為經(jīng)濟(jì)損失，m為地震級(jí)數(shù)，k與B為常數(shù)，k大于零。在此假設(shè)下，將年度地震頻數(shù)下的不同震級(jí)進(jìn)行加總，即可大體衡量年度地震對(duì)中國(guó)造成的經(jīng)濟(jì)損失。年度震級(jí)累積和越大，所造成的損失也就越大。采用年度震級(jí)和的原因如下:1)關(guān)于震級(jí)的資料較為完整，數(shù)據(jù)較多，保證了擬合的精度;2)以震級(jí)為衡量標(biāo)準(zhǔn)，排除了以損失額為標(biāo)準(zhǔn)受到的通貨膨脹、人口增長(zhǎng)、財(cái)產(chǎn)價(jià)值變動(dòng)等因素帶來(lái)的干擾;3)劃分風(fēng)險(xiǎn)損失分擔(dān)機(jī)制重點(diǎn)是基于一定風(fēng)險(xiǎn)容忍度下各個(gè)主體的分擔(dān)比例，分擔(dān)額度相對(duì)次要。

模擬年度地震震級(jí)和的具體步驟為:首先由地震頻數(shù)發(fā)生器產(chǎn)生一個(gè)年度地震頻次為f(i)的結(jié)果。然后將其作為地震震級(jí)發(fā)生器的模擬次數(shù)，依托地震震級(jí)的離散分布進(jìn)行模擬，模擬次數(shù)為f(i)次。最后將f(i)個(gè)地震級(jí)數(shù)進(jìn)行加總，得到年度地震震級(jí)和mag。將上述結(jié)果模擬10000次，可以得出年度地震震級(jí)和的頻率圖。圖9、10分別是基于泊松分布與基于負(fù)二項(xiàng)分布頻數(shù)發(fā)生器產(chǎn)生的年度地震震級(jí)和頻率圖。可以看出，泊松分布明顯比負(fù)二項(xiàng)分布保守，負(fù)二項(xiàng)分布對(duì)低頻數(shù)與高頻數(shù)均有所涉及。因此，可以把負(fù)二項(xiàng)分布看作極端情況，把泊松分布看作一般情況。

圖9 泊松分布下的年度震級(jí)和頻數(shù)圖Fig.9 Frequency of total magnitude in 1 year based on poisson distribution

圖10 負(fù)二項(xiàng)分布下的年度震級(jí)和頻數(shù)圖Fig.10 Frequency of total magnitude in 1 year based on negative binomial distribution

3.4 地震風(fēng)險(xiǎn)損失的超越概率曲線

由上文的討論可知，超越概率曲線是F(x)=p(ε≥x)的函數(shù)圖。超越概率曲線的優(yōu)點(diǎn)在于評(píng)估地震風(fēng)險(xiǎn)以及作相應(yīng)的決策時(shí)更具直觀效果。在具有年度地震累積震級(jí)分布的基礎(chǔ)上，計(jì)算每一地震震級(jí)和發(fā)生的頻率，便可得到地震風(fēng)險(xiǎn)損失的超越概率曲線。圖11、12分別為基于泊松分布與基于負(fù)二項(xiàng)分布的地震風(fēng)險(xiǎn)損失超越概率曲線。橫軸為地震震級(jí)累積和，縱軸為超越概率。可以看出，泊松分布下的最大震級(jí)累積和為341.6，遠(yuǎn)遠(yuǎn)小于負(fù)二項(xiàng)分布產(chǎn)生的1125。因此，可以用泊松分布做一般解釋，負(fù)二項(xiàng)分布做極端情況下的解釋。

4 地震風(fēng)險(xiǎn)損失分擔(dān)機(jī)制設(shè)計(jì)

圖11 泊松分布下的超越概率曲線Fig.11 Exceedance probability curve based on poisson distribution

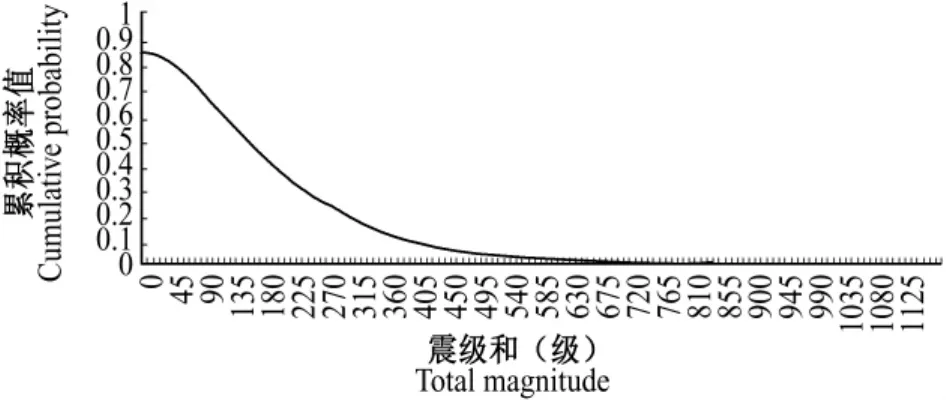
圖12 負(fù)二項(xiàng)分布下的超越概率曲線Fig.12 Exceedance probability curve based on negative binomial distribution

在采用超越概率曲線對(duì)地震風(fēng)險(xiǎn)進(jìn)行評(píng)估之后，便可以劃分地震風(fēng)險(xiǎn)損失的分擔(dān)機(jī)制。在劃分分擔(dān)機(jī)制之前，首先要明確分擔(dān)機(jī)制的參與主體。在對(duì)國(guó)外巨災(zāi)風(fēng)險(xiǎn)損失分擔(dān)機(jī)制研究的基礎(chǔ)上，得出不同國(guó)家均有以下主體參與:個(gè)人、保險(xiǎn)市場(chǎng)(保險(xiǎn)人與再保險(xiǎn)人)、政府與資本市場(chǎng)。鑒于我國(guó)資本市場(chǎng)還處于初級(jí)階段，巨災(zāi)債券等巨災(zāi)資本品還未出臺(tái)，因此這里先不考慮資本市場(chǎng)對(duì)于巨災(zāi)風(fēng)險(xiǎn)損失的分擔(dān)。其次是各個(gè)主體的風(fēng)險(xiǎn)容忍度問題。目前關(guān)于各主體的最優(yōu)承擔(dān)額度學(xué)術(shù)界還未得出一個(gè)很好的結(jié)果，但是通過Cummins等［5］提供的巨災(zāi)風(fēng)險(xiǎn)承保能力模型進(jìn)行測(cè)算，可以得出在個(gè)人承擔(dān)10%地震風(fēng)險(xiǎn)的基礎(chǔ)上，我國(guó)財(cái)險(xiǎn)市場(chǎng)(保險(xiǎn)人與再保險(xiǎn)人)目前能夠承擔(dān)36%的風(fēng)險(xiǎn)損失，剩下的須由政府或者其他機(jī)構(gòu)承擔(dān)［14］。下圖為假設(shè)個(gè)人承擔(dān)超越概率大于0.9的風(fēng)險(xiǎn)、政府承擔(dān)超越概率小于0.1的風(fēng)險(xiǎn)(其中保險(xiǎn)人承擔(dān)超越概率大于0.5以上的部分，再保險(xiǎn)人承擔(dān)超越概率小于0.5以下的部分)的分擔(dān)機(jī)制。

由于負(fù)二項(xiàng)分布的擬合效果較好，因此先分析通過負(fù)二項(xiàng)分布產(chǎn)生的地震風(fēng)險(xiǎn)損失分擔(dān)機(jī)制(圖13)。第一層由個(gè)人承擔(dān)，劃分依據(jù)是超越概率大于0.9的地震風(fēng)險(xiǎn)損失。這種損失發(fā)生的較為頻繁，應(yīng)該由個(gè)人承擔(dān)，這樣既緩解了保險(xiǎn)市場(chǎng)與政府的壓力，又提高了個(gè)人防災(zāi)減災(zāi)的積極性;其次，政府應(yīng)當(dāng)承擔(dān)十年一遇以及大于十年一遇的所有風(fēng)險(xiǎn)損失，即超越概率大于0.1的地震風(fēng)險(xiǎn)損失。政府應(yīng)該作為巨災(zāi)風(fēng)險(xiǎn)最后的承擔(dān)者，承擔(dān)市場(chǎng)與個(gè)人無(wú)法承擔(dān)的部分，這是其他國(guó)家的經(jīng)驗(yàn)，也是政府職責(zé)的所在。剩下的部分可以由保險(xiǎn)市場(chǎng)來(lái)承擔(dān)，具體保險(xiǎn)人與再保險(xiǎn)人該如何劃分，此處假設(shè)保險(xiǎn)人承擔(dān)超越概率大于0.5以上的部分，再保險(xiǎn)人承擔(dān)超越概率小于0.5以下的部分。因此，得出在最大震級(jí)和為1125的情況下，個(gè)人承擔(dān)5%，保險(xiǎn)人承擔(dān)12%，再保險(xiǎn)人承擔(dān)20%，政府承擔(dān)63%。

圖13 基于負(fù)二項(xiàng)分布的地震風(fēng)險(xiǎn)損失分擔(dān)機(jī)制Fig.13 Earthquake risk loss sharing mechanism based on negative binomial distribution

依據(jù)泊松分布劃分地震風(fēng)險(xiǎn)損失分擔(dān)機(jī)制時(shí)，在假設(shè)的風(fēng)險(xiǎn)容忍度下，個(gè)人可以自留46%，政府承擔(dān)30%，保險(xiǎn)市場(chǎng)只承擔(dān)很小部分(圖14)。與負(fù)二項(xiàng)分布下的結(jié)果對(duì)比，說(shuō)明:隨著地震風(fēng)險(xiǎn)方差的增加，個(gè)人與保險(xiǎn)市場(chǎng)愿意承擔(dān)的風(fēng)險(xiǎn)越來(lái)越小，政府應(yīng)該承擔(dān)的風(fēng)險(xiǎn)越來(lái)越大。這與學(xué)術(shù)界呼吁政府參與巨災(zāi)保險(xiǎn)制度的結(jié)論一致。

圖14 基于泊松分布的地震風(fēng)險(xiǎn)損失分擔(dān)機(jī)制Fig.14 Earthquake risk loss sharing mechanism based on poisson distribution

對(duì)于不同風(fēng)險(xiǎn)容忍度的假設(shè)會(huì)導(dǎo)致不同的分擔(dān)結(jié)果，圖15列示了基于負(fù)二項(xiàng)分布的保險(xiǎn)市場(chǎng)分擔(dān)比例。由圖可以看出，在個(gè)人風(fēng)險(xiǎn)容忍度不變的情況下政府容忍度的增加使得保險(xiǎn)市場(chǎng)需要承擔(dān)的比例減少。在政府容忍度不變的情況下，個(gè)人容忍度的減少(即個(gè)人對(duì)于巨災(zāi)風(fēng)險(xiǎn)承受意愿增加)使得保險(xiǎn)市場(chǎng)承擔(dān)的比例減少。

圖15 不同政府容忍度與個(gè)人容忍度下保險(xiǎn)市場(chǎng)的分擔(dān)比例Fig.15 Sharing ratio of insurance market based on different government and individual risk bearing

5 結(jié)論

本文采用隨機(jī)模擬技術(shù)對(duì)我國(guó)的地震風(fēng)險(xiǎn)進(jìn)行了評(píng)估，并以超越概率曲線的形式進(jìn)行了反映。隨機(jī)模擬技術(shù)所采用的數(shù)據(jù)來(lái)自中國(guó)地震臺(tái)網(wǎng)中心，時(shí)間跨度為100年，具有一定的可靠性。隨機(jī)模擬技術(shù)具體采用的是復(fù)合泊松模型與復(fù)合負(fù)二項(xiàng)模型，前者較后者保守，反映了地震風(fēng)險(xiǎn)的一般情況，而后者能更好的反映地震風(fēng)險(xiǎn)的極端情況。文中所指地震風(fēng)險(xiǎn)損失以年度震級(jí)和來(lái)表示，震級(jí)累積和越高，表明地震風(fēng)險(xiǎn)損失越大。

在繪制出地震風(fēng)險(xiǎn)損失的超越概率曲線的情況下，首先，假設(shè)超越概率 0.9、0.5、0.1 作為分擔(dān)層次的劃分依據(jù)，以此設(shè)計(jì)出了一個(gè)包含個(gè)人、保險(xiǎn)人、再保險(xiǎn)人與政府的四層地震風(fēng)險(xiǎn)損失分擔(dān)機(jī)制。在泊松分布下，個(gè)人與保險(xiǎn)人可以承擔(dān)70%的風(fēng)險(xiǎn)損失，政府只需承擔(dān)30%的風(fēng)險(xiǎn)損失;在負(fù)二項(xiàng)分布下，政府需要承擔(dān)絕大多數(shù)風(fēng)險(xiǎn)損失(65%)。說(shuō)明巨災(zāi)風(fēng)險(xiǎn)的方差越大，個(gè)人與保險(xiǎn)人越難以應(yīng)對(duì)，政府參與風(fēng)險(xiǎn)損失分擔(dān)機(jī)制越具有必然性。其次，本文分別通過圖表形式反映了政府容忍度分別為0.1、0.2、0.3、0.4 下個(gè)人容忍度與保險(xiǎn)市場(chǎng)分擔(dān)比例的關(guān)系。

本文的主要目的在于提供一個(gè)通過隨機(jī)模擬技術(shù)對(duì)巨災(zāi)風(fēng)險(xiǎn)進(jìn)行評(píng)估，進(jìn)而對(duì)巨災(zāi)風(fēng)險(xiǎn)損失分擔(dān)機(jī)制進(jìn)行劃分的方法。超越概率曲線具有較強(qiáng)的直觀性，在具備確定的風(fēng)險(xiǎn)容忍度的條件下，通過隨機(jī)模擬技術(shù)下的超越概率曲線做決策具有一定的合理性。隨機(jī)模擬技術(shù)可以針對(duì)不同的巨災(zāi)風(fēng)險(xiǎn)，產(chǎn)生不同的超越概率曲線，以反映不同巨災(zāi)風(fēng)險(xiǎn)的特點(diǎn)。所劃分的巨災(zāi)風(fēng)險(xiǎn)損失分擔(dān)機(jī)制依賴于各個(gè)主體的風(fēng)險(xiǎn)容忍度，本文只呈現(xiàn)了不同風(fēng)險(xiǎn)容忍度下各個(gè)主體的分擔(dān)比例，缺乏對(duì)最優(yōu)風(fēng)險(xiǎn)容忍度的探討，這也是今后進(jìn)一步研究的方向。

References)

［1］謝世清.巨災(zāi)壓力下的公共財(cái)政:國(guó)際經(jīng)驗(yàn)與啟示［J］.當(dāng)代財(cái)經(jīng)，2009，(2):36－ 40.［Xie Shiqing.Public Finance with Catastrophe:International Experience and Suggestion［J］.Modern Finance and Economy，2009，(2):36－40.］

［2］姚慶海.沉重叩問:巨災(zāi)肆虐，我們將何為?［J］.交通企業(yè)管理，2006，(10):30.［Yao Qinghai.Heavy Inquiries:How Can We Deal with Catastrophe?［J］.Transportation Enterprise Management，2006，(10):30.］

［3］卓志，吳婷.中國(guó)地震巨災(zāi)保險(xiǎn)制度的模式選擇與設(shè)計(jì)［J］.中國(guó)軟科學(xué)，2011，(1):17－24.［Zhuo Zhi，Wu Ting.Selection and Design for Earthquake Catastrophe Insurance System in China ［J］.China Soft Science，2011，(1):17－24.］

［4］趙苑達(dá).巨災(zāi)保險(xiǎn)制度模式分析與我國(guó)巨災(zāi)保險(xiǎn)制度的架構(gòu)［J］.財(cái)貿(mào)經(jīng)濟(jì)，2009，(9):70－76.［Zhao Yuanda.Analysis on Catastrophe Insurance Pattern and Design for China’s Pattern ［J］.Finance＆Trade Economics.2009，(9):70－76.］

［5］Cummins J D，Doherty N，Lo A.Can Insurers Pay for the‘big one’?Measuring the Capacity of the Insurance Market to Respond to Catastrophic Losses［J］.Journal of Banking ＆ Finance，2002，26(2):557－583.

［6］Niehaus G.The Allocation of Catastrophe Risk［J］.Journal of Banking＆ Finance，2002，26(2):585－596.

［7］Swiss R E.Disaster Risk Financing:Reducing the Burden on Public Budgets［R］.Swiss Re Focus Report，2008.

［8］Cummins J D.CAT Bonds and Other Risk-Linked Securities:State of the Market and Recent Developments［J］.Risk Management and Insurance Review，2008，11(1):23－47.

［9］Clarke D，Grenham D.Migration and Global Environmental Change［R］.Working Paper，2011.

［10］Tsai C H，Chen C W.An Earthquake Disaster Management Mechan-ism Based on Risk Assessment Information for the Tourism Industry—A Case Study from the Island of Taiwan［J］.Tourism Management，2010，31(4):470－481.

［11］中國(guó)精算師協(xié)會(huì).精算模型［M］.北京:中國(guó)財(cái)政經(jīng)濟(jì)出版社，2010.［CAA.Actuarial Models［M］.Beijing:China Financial＆Economic Publishing House，2010.］

［12］中國(guó)地震臺(tái)網(wǎng)中心［DB/OL］.http://www.cenc.ac.cn/.［CENC［DB/OL］.http://www.cenc.ac.cn］

［13］樓寶棠.中國(guó)古今地震災(zāi)情總匯［M］.北京:地震出版社，1996.［Lou Baotang.A Comprehensive Compilation of Historic and Recent Earthquakes Disaster Status in China［M］.Beijing:Dizhen Press，1996.］

［14］姚鵬.我國(guó)巨災(zāi)風(fēng)險(xiǎn)損失分擔(dān)機(jī)制研究［D］.武漢:武漢大學(xué)，2012.［Yao Peng.Study on the Sharing Mechanisms of Catastrophe Risk Loss in China［D］.Wuhan:Wuhan University，2012.］