基于稀疏重建和壓縮感知波束形成的高分辨DOA估計(jì)

陳玉鳳, 黃建國, 蘇建軍

?

基于稀疏重建和壓縮感知波束形成的高分辨DOA估計(jì)

陳玉鳳, 黃建國, 蘇建軍

(西北工業(yè)大學(xué) 航海學(xué)院, 陜西 西安, 710072)

利用空域目標(biāo)的稀疏性，建立了基于正弦域的DOA壓縮感知模型，并根據(jù)壓縮感知理論設(shè)計(jì)了一種隨機(jī)壓縮采樣方式，從而構(gòu)造了一種新的測量矩陣。同時(shí)將普適的高斯隨機(jī)測量矩陣進(jìn)行近似QR分解得到新的測量矩陣，使得該矩陣具有更好的約束等容(RIP)常數(shù)。應(yīng)用新構(gòu)造的測量矩陣，采用奇異值分解(SVD)提取信號子空間，得到低維形式的接收數(shù)據(jù)矩陣，從而提出了2種不同類別的DOA估計(jì)算法：基于QR分解和奇異值分解的多測量矢量欠定系統(tǒng)正則化聚焦求解算法(QR-SVD-MFOCUSS)和壓縮感知波束形成算法(RSVD-CSB、QRSVD-CSB)。與多測量矢量欠定系統(tǒng)聚焦求解(MFOCUSS)等算法相比，QR-SVD-MFOCUSS算法在低信噪比條件下適用且運(yùn)算量顯著降低；與傳統(tǒng)的最小方差無畸變響應(yīng)(MVDR)算法和壓縮感知(CS)波束形成算法相比，基于隨機(jī)測量矩陣和奇異值分解的壓縮感知波束形成算法(RSVD-CSB)和基于QR分解測量矩陣和奇異值分解的壓縮感知波束形成算法(QRSVD-CSB)算法具有更高的角度分辨率、更低的均方根誤差及更優(yōu)的估計(jì)性能等。

方位估計(jì); 壓縮感知; QR分解; 波束形成

0 引言

波達(dá)方向估計(jì)(direction-of-arrival, DOA)是高分辨陣列信號處理的重要研究內(nèi)容之一, 被廣泛的應(yīng)用于聲源定位、無線通信、雷達(dá)、聲納和無線神經(jīng)網(wǎng)絡(luò)等諸多領(lǐng)域[1-2]。在過去的幾十年中, 有關(guān)學(xué)者研究和分析了大量有效的DOA估計(jì)算法, 其中有Capon提出的波束形成方法[3]以及Schimidt提出的多重信號分類法(multiple signal classification, MUSIC)[4]為代表的子空間類算法。但是, 這些方法都必須依靠數(shù)據(jù)的統(tǒng)計(jì)性能。因此, 算法的性能會(huì)隨著樣本數(shù)量的減少或者是信噪比的降低而急劇下降。由Donoho與Candes等人提出的壓縮感知(compressed sensing, CS)[5-6]理論是一個(gè)充分利用信號稀疏性或可壓縮性的全新信號采集、編碼理論。該理論表明, 當(dāng)信號具有稀疏性或是可壓縮性時(shí), 通過采集少量的信號投影值就可實(shí)現(xiàn)信號的準(zhǔn)確或近似重構(gòu)。

近幾年, 基于壓縮感知的DOA估計(jì)得到了廣泛的研究。文獻(xiàn)[7]利用空間的稀疏性, 提出了基于奇異值分解(singular value decomposition, SVD)的1重構(gòu)算法來實(shí)現(xiàn)DOA估計(jì)。該算法在已知信號源個(gè)數(shù)的先驗(yàn)信息條件下具有良好的估計(jì)性能, 即使在信號相關(guān)或是信號的角度間距很小的情況下, 依然具有較高的角度分辨率。但是, 當(dāng)信號源個(gè)數(shù)未知時(shí), 算法的性能則急劇下降。Cevher[8-9]等人利用多個(gè)時(shí)刻的陣元接收數(shù)據(jù)的隨機(jī)投影和由一個(gè)參考陣元得到的完整的波形記錄, 重構(gòu)一個(gè)稀疏的角空間場景, 從而實(shí)現(xiàn)了DOA估計(jì)。

隨著研究的不斷深入, 研究人員開始采用貝葉斯模型進(jìn)行信號重建。文獻(xiàn)[10]在已知逆伽瑪先驗(yàn)信息的前提下推導(dǎo)出基于多層遞階的壓縮感知貝葉斯模型。而文獻(xiàn)[11]則通過硬闕值迭代克服了基于壓縮感知貝葉斯模型的DOA估計(jì)中的協(xié)方差矩陣奇異的缺點(diǎn)。

本文通過對基于壓縮感知的DOA估計(jì)的研究, 提出了2種新的基于壓縮感知的高分辨DOA估計(jì)算法, 其中一種根據(jù)壓縮感知理論, 利用空域信號的稀疏性, 采用構(gòu)造的壓縮測量矩陣對空間信號進(jìn)行壓縮采樣; 另一種是基于QR分解和奇異值分解的多測量矢量欠定系統(tǒng)正則化聚焦求解(QR singular value decomposition multivectors FOCal undetermined system solver, QR-SVD- MFOCUSS)算法、基于最小方差無畸變響應(yīng)(mi- nimum variance distortionless response, MVDR)的壓縮感知波束形成和基于隨機(jī)測量矩陣和奇異值分解的壓縮感知波束形成(random singular value decomposition compressive sensing beamforming, RSVD-CSB)算法及基于QR分解測量矩陣和奇異值分解的壓縮感知波束形成(QR singular value decomposition compressive sensing beamforming, QRSVD-CSB)算法。與多測量矢量欠定系統(tǒng)聚焦求解(multi-vectors FOCal undetermined system solver, MFOCUSS)算法比, QR- SVD-MFOCUSS算法在低信噪比下適用且運(yùn)算量顯著降低; 與傳統(tǒng)的MVDR算法和CS波束形成算法相比, RSVD-CSB算法和QRSVD-CSB算法具有更高的角度分辨率和更優(yōu)的性能。

1 CS基本原理和信號建模

1.1 CS基本原理

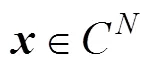
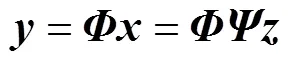
考慮加性噪聲, 式(1)可進(jìn)一步表示為

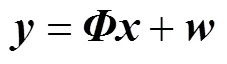
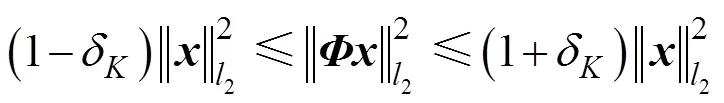
1.2 問題描述

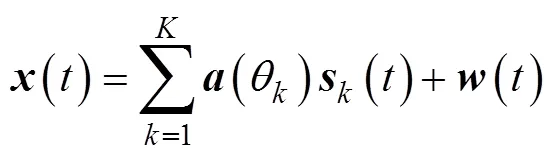
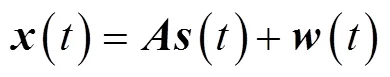
1.3 基于正弦域的DOA估計(jì)模型

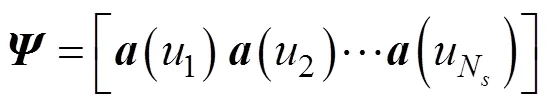
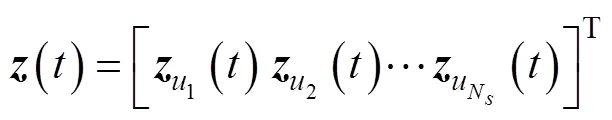
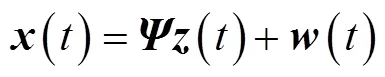
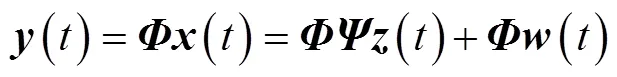
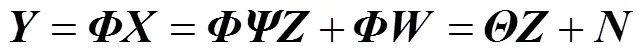
由等正弦劃分得到的陣列流行矩陣比等角度劃分得到的陣列流行具有更加顯著的近似正交性和更小的相關(guān)性因子, 因此更加滿足RIP和互不相干特性(mutual incoherence property，MIP)條件, 稀疏重建性能更優(yōu)。

2 測量矩陣的構(gòu)造

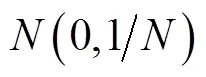
根據(jù)壓縮感知理論中對測量矩陣的要求設(shè)計(jì)了2種新的測量矩陣。

2.1 隨機(jī)測量矩陣

本節(jié)提出了一種新的壓縮采樣的方式, 該采樣方法有效地減小了陣列結(jié)構(gòu)的尺寸, 降低了運(yùn)算量。對應(yīng)測量矩陣構(gòu)造過程如下。

顯然本節(jié)的測量矩陣符合RIP條件。

2.2 基于QR分解的高斯矩陣

3 SVD-MFOCUSS 和CS波束形成

3.1 SVD-MFOCUSS

對式(11)的陣列接收數(shù)據(jù)進(jìn)行SVD分解

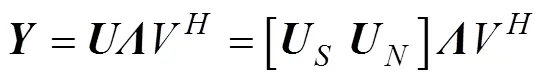
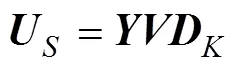
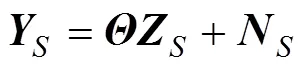
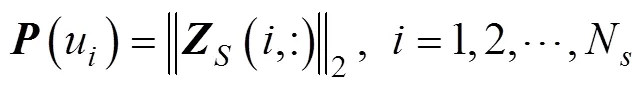
3.2 基于壓縮感知的波束形成

通過波束形成的方法推導(dǎo)基于壓縮感知的角譜估計(jì)公式。由MVDR算法推導(dǎo)出基于壓縮感知的角譜估計(jì)公式

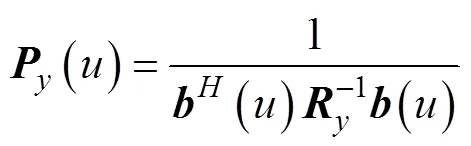
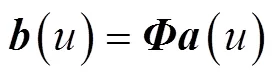
4 仿真結(jié)果與分析

通過仿真非相干信號的相近目標(biāo)和遠(yuǎn)離目標(biāo)等多種信號來驗(yàn)證算法的有效性, 并與傳統(tǒng)的MVDR算法、CS波束形成算法相比較分析算法性能。采用均方根誤差作為算法性能的指標(biāo), DOA估計(jì)的均方根誤差定義為

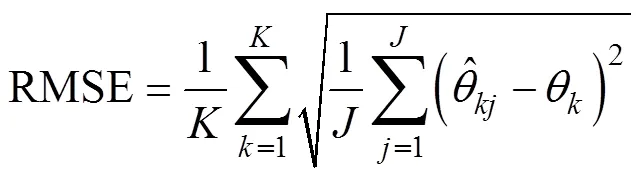
圖1為采用QR-SVD-MFOCUSS算法和MVDR算法得到的角譜估計(jì)。從圖中可看出, QR- SVD-MFOCUSS算法能夠?qū)?個(gè)非常鄰近的目標(biāo)進(jìn)行有效分辨, 而MVDR算法無法分辨2個(gè)非常鄰近的目標(biāo), 說明QR-SVD-MFOCUSS算法比MVDR算法具有更高的角度分辨率。

試驗(yàn)2: 圖2分別采用MVDR算法、RSVD- CSB 算法、QRSVD-CSB算法和CSB算法的空域譜輸出對比。由圖可知, 與CSB算法相比, RSVD-CSB 算法和QRSVD-CSB算法具有更尖銳的譜峰、更低的旁瓣; 與MVDR算法相比, RSVD-CSB 算法和QRSVD-CSB算法具有更高的角度分辨率。

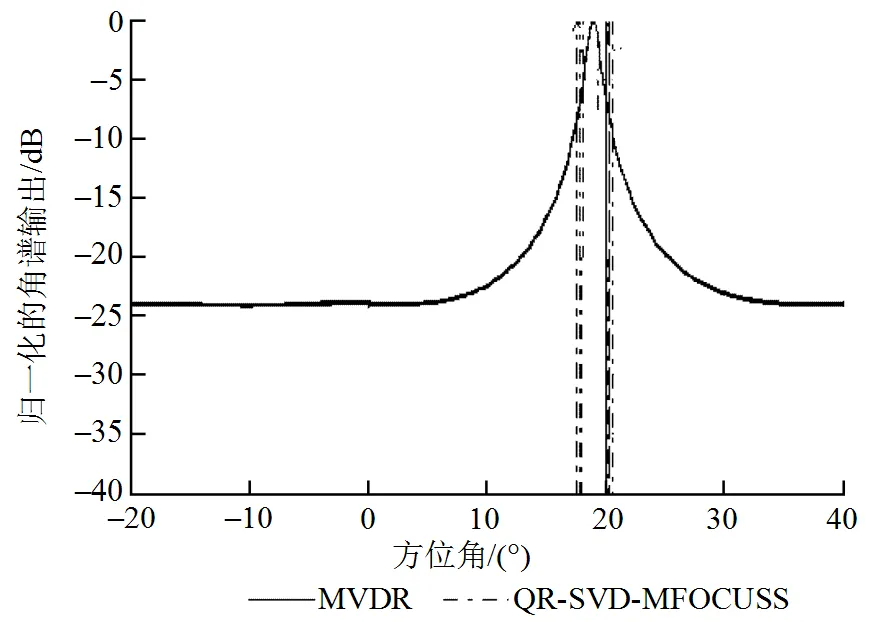
圖1 采用QR-SVD-MFOCUSS算法和MVDR算法獲得的鄰近非相干信號的空域譜輸出

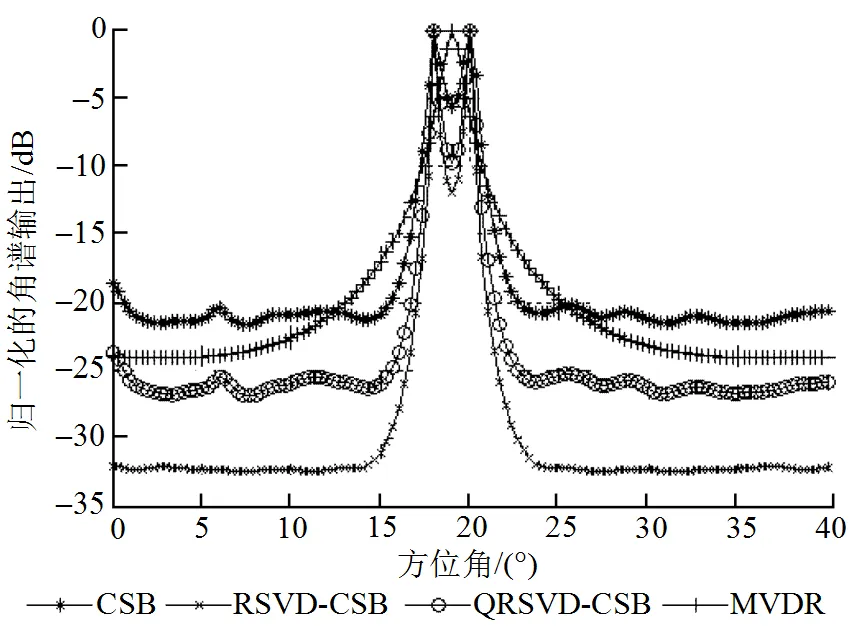
圖2 采用MVDR, RSVD-CSB, QRSVD-CSB和CSB算法所獲得的鄰近非相干信號的空域譜輸出

圖4為入射方位角在[8o, 20o]時(shí), 各種算法DOA估計(jì)的均方根誤差隨信噪比變化的關(guān)系曲線。從圖4可知, 當(dāng)信噪比較高時(shí), 各種算法均能對目標(biāo)角度進(jìn)行正確估計(jì), 但是隨著信噪比的降低, MVDR算法性能不斷下降, 而RSVD-CSB 算法和QRSVD-CSB算法在低信噪比的情況下仍然具有較好的估計(jì)性能, 且明顯小于MVDR的DOA估計(jì)均方根誤差。當(dāng)信噪比低于－15 dB時(shí), QRSVD-CSB算法估計(jì)性能急劇下降。

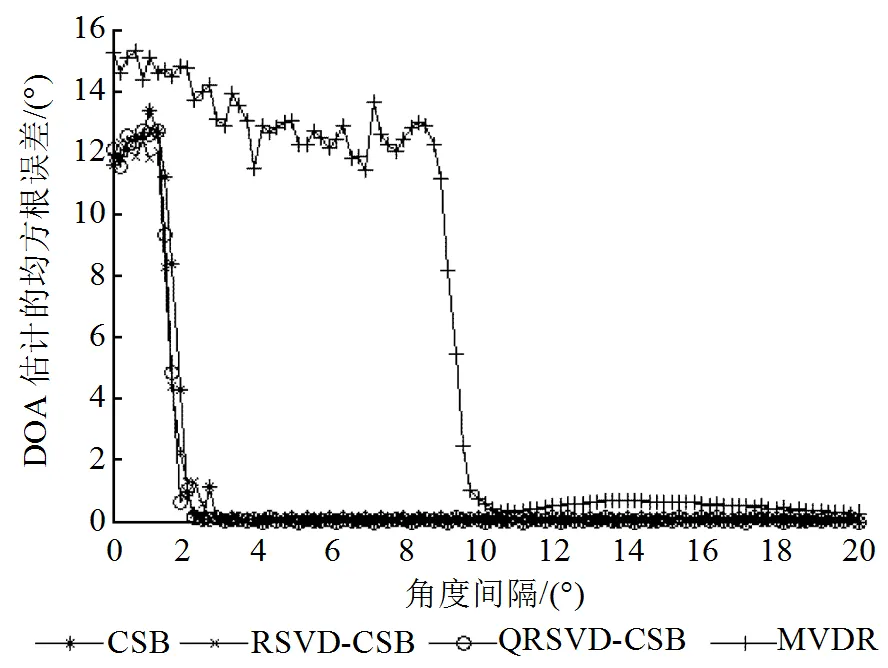
圖3 DOA估計(jì)的均方根誤差隨角度間隔變化曲線

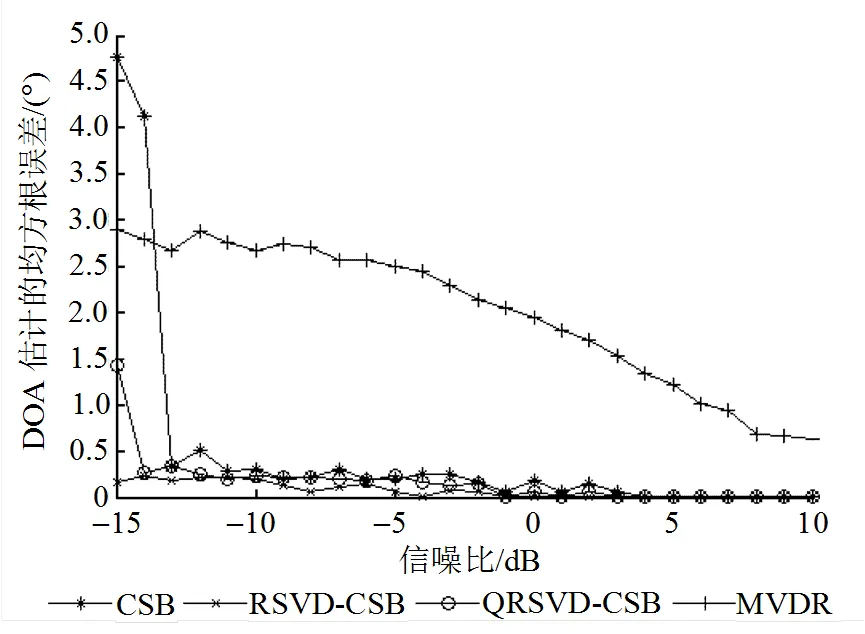
圖4 DOA估計(jì)的均方根誤差隨信噪比變化曲線

5 結(jié)束語

本文提出了2種新的測量矩陣, 一種是設(shè)計(jì)新的壓縮采樣方式, 另一種則為基于近似QR分解的高斯隨機(jī)測量矩陣。根據(jù)這2種新的測量矩陣, 分別采用壓縮感知的重構(gòu)算法和壓縮感知的波束形成算法計(jì)算角譜, 從而得到DOA估計(jì)角度。比較傳統(tǒng)的MVDR算法, 本文提出的QR-SVD-MFOCUSS算法、RSVD-CSB 算法和QRSVD-CSB算法具有更高的角度分辨率, 在低信噪比時(shí)具有更加穩(wěn)定的性能, 同時(shí)顯著縮減了計(jì)算量。

[1] Krim H, Viberg H. Two Decades of Array Signal Processing Research: the Parametric Approach[J]. IEEE Signal Processing Magazine, 1996, 13(4): 67-94.

[2] Stoica P, Moses R. Introduction to Spectral Analysis[M]. 2th ed. Upper Saddle River. NJ: Prentice-Hall, 2004.

[3] Capon J. High-Resolution Frequency-Wave number Spectrum Analysis[J]. Proceeding of the IEEE, 1969, 57(10): 1110-1125.

[4] Schmit R. Multiple Emitter Location and Signal Parameter Estimation[J]. IEEE Transaction on Antennas and Propagation, 1986, 34(3): 276-280.

[5] Donoho D. Compressed Sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306.

[6] Candes E, Romberg J, Tao T. Robust Uncertainty Principles: Exact Signal Reconstruction from Highly in Complete Frequency Information[J]. IEEE Transactions On Information Theory, 2006, 52(2): 489-509.

[7] Malioutov D, ?etin M, Willsky S A. A Sparse Signal Reconstru- ction Perspective for Source Localization with Sensor Arrays [J]. IEEE Transactions Signal Processing, 2005, 53(8): 3010-3022.

[8] Gurbuz A, Cevher V, McClellan J. Compressive Beamforming Method[C]//IEEE International Conference on Acoustics, Speech and Signal Processing, 2008: 2617-2620.

[9] Cevher V, Gurbuz A, McClellan J, et al. Compressive Wireless Arrays for Bearing Estimation[C]//IEEE International Conference on Acoustics Speech and Signal Processing, 2008: 2497-2500.

[10] Ji S, Xue Y, Carin L. Bayesian Compressive Sensing[J]. IEEE Transactions Signal Processing, 2008, 56(6): 2346-2356.

[11] Sun L, Wang H L. Direction-of-Arrive Estimation Based on Modified Bayesian Compressive Sensing Method[C]//Proceeding on WCSP, 2011: 1-4.

[12] Candes E J, Wakin M B. An Introduction to Compressive Sampling[J]. IEEE Signal Processing Magazine, 2008, 25(2): 21-30．

[13] Szarek S. Condition Numbers of Random Matrices[J]. Jou- rnal of Complexity, 1991, 7(2): 131-149.

[14] Cand S E, Tao T. Decoding by Linear Programming[J]. IEEE Transactions on Information Theory, 2004, 51(12): 4203- 4215.

[15] Catter S F, Rao B D, Engan K, et al. Sparse Solution to Linear Inverse Problems with Multiple Measurement Vertors[J].IEEE Transaction on Signal Processing, 2005, 53(7): 2477-2488.

High Resolution Direction-of-Arrive Estimation Based on Sparse Reconstruction and Compressive Sensing Beamforming

CHEN Yu-feng, HUANG Jian-guo, SU Jian-jun

(College of Marine Engineering, Northwestern Ploytechnical University, Xi′an 710072, China)

A novel compression perception model is established by making use of the spatial sparsity. A random compression matrix is constructed by designing a new compressive sampling way with compressive sensing(CS) theory. And another compression matrix is obtained by applying approximate QR decomposition to Gaussian random matrix in order to get a better restricted isometry property(RIP) constant. Singular value decomposition(SVD) is adopted on the data matrix to extract signal subspace for getting low dimensional form of receiving data matrix. Two different kinds of methods for DOA estimation are proposed based on the new compression matrices. One is for CS recovery, i.e. QR singular value decomposition multi-vectors FOCal undetermined system solve(QR-SVD-MFOCUSS); the other is for CS beamforming, i.e. random singular value decomposition compressive sensing beamforming(RSVD-CSB) and QR singular value decomposition compressive sensing beamforming(QRSVD-CSB). Simulation results show that, compared to the multi-vectors FOCal undetermined system solver(MFOCUSS) algorithms, QR-SVD-MFOCUSS is suitable for low signal-to-noise ratio(SNR) condition with significant reduction of computational burden; and compared to the minimum variance distortionless response(MVDR) algorithms and the CS beamforming algorithms, the proposed method possesses higher angular resolution, lower root mean square error(RMSE), better estimation performance, and so on.

direction-of-arrival estimation; compressive sensing(CS); QR decomposition; compressive sensing(CS) beamforming

TJ630.34; TN911.7

A

1673-1948(2013)02-0110-05

2012-05-12;

2012-06-28.

國家自然科學(xué)基金(60972152); 國家重點(diǎn)實(shí)驗(yàn)室基金(9140C230309110C23); 西北工業(yè)大學(xué)基礎(chǔ)研究基金(JC201027).

陳玉鳳(1986-), 女, 在讀碩士, 主要研究方向?yàn)樾盘柵c信息處理.

(責(zé)任編輯: 楊力軍)