PZT壓電式微傳感器的結(jié)構(gòu)優(yōu)化

田開云，譚曉蘭

（北方工業(yè)大學(xué)機電工程學(xué)院，北京 100041）

0 引言

目前，MEMS壓力傳感器[1]應(yīng)用比較多的有壓阻式壓力傳感器和電容式壓力傳感器，應(yīng)用壓電效應(yīng)制成的壓電式微傳感器[2]由于不僅可以作為傳感器，在輸入電荷產(chǎn)生電場的情況下，還可以作為制動器，因此，壓電式微傳感器具有廣闊的應(yīng)用前景[3]。

目前對于壓電懸臂梁式微傳感器[4-5]的優(yōu)化主要集中在假設(shè)形狀已經(jīng)確定的條件下（一般為矩形），通過改變復(fù)合懸臂梁的某一尺寸參數(shù)為變量，其他保持不變的情況下，得出該尺寸參數(shù)對輸出電壓的影響。但由于在優(yōu)化分析前已固定復(fù)合懸臂梁的結(jié)構(gòu)為矩形線性結(jié)構(gòu)，因此從理論上來說并不能保證所得到結(jié)果為最優(yōu)結(jié)果。

本文試圖在已經(jīng)給定壓電材料用量的情況下，通過建立數(shù)學(xué)模型，并用遺傳算法對模型進行求解，得出壓電懸臂梁的最佳長度l，和偏轉(zhuǎn)角度α，在不改變各層厚度的情況下，得出最大的感應(yīng)電荷，從而保證在力F 一定的情況下，能夠提高傳感器的靈敏度。

1 壓電懸臂梁式微傳感器的工作原理與彎曲特性仿真

1.1 工作原理

當(dāng)微懸臂梁的端部受到作用力時，梁會發(fā)生彎曲形變。梁中的壓電ZnO 薄膜層在受到力的作用時，由壓電效應(yīng)，會在z 軸方向產(chǎn)生極化電荷。通過上、下電極層將電荷導(dǎo)出并輸入到電荷放大器（或電流放大器），再將電荷信號放大并轉(zhuǎn)換成電壓信號進行信號處理。

1.2 壓電懸臂梁彎曲特性仿真

為了得到壓電材料在懸臂梁結(jié)構(gòu)時，自由端受力時產(chǎn)生的感應(yīng)電荷分布，先建一個簡單模型對壓電懸臂梁材料的彎曲特性進行模擬仿真，如圖1 所示，紅色部分為底電極，上部分開間隔的各自獨立的上電極，長度50 mm，厚度1 mm，在懸臂梁的末端施加100 μN 的壓力后，仿真得到懸臂粱的彎曲曲線分別為圖2和圖3。

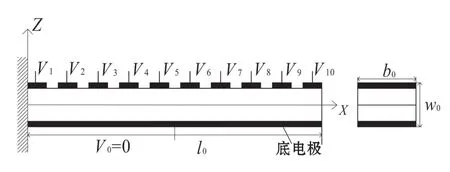
圖1 壓電懸臂梁仿真模型

如圖2 所示的懸臂梁在固支端A 附近的應(yīng)變最小，在自由端B 處的應(yīng)變最大，而圖3 則顯示出在B處的電壓最小，近乎為0，反而在固支端A附近的電壓達到最大值。

因此，如果把懸臂梁做成矩形式的線性結(jié)構(gòu)，并不能有效改善提高傳感器的靈敏度[6]。因此必須結(jié)合形狀優(yōu)化來綜合提高傳感器的靈敏度。

圖2 懸臂粱的彎曲曲線

圖3 懸臂梁電壓分布曲線

2 變截面式壓電微傳感器的建模與優(yōu)化

2.1 建模

由1.2 對壓電微懸臂梁的彎曲特性仿真可知，懸臂梁根部靠近固定裝置的一側(cè)，產(chǎn)生的感應(yīng)電荷最多，而在施加力的自由端一側(cè)產(chǎn)生的感應(yīng)電荷極少，末端甚至幾乎為0，又由于傳感器的靈敏度為：

由公式（1）可知，在自由端載荷F 不變的情況下，壓電懸臂梁產(chǎn)生的感應(yīng)電荷越多，則靈敏度越大。

本文的創(chuàng)新點在于：設(shè)計了一般情況下的變截面復(fù)合懸臂梁，并建立優(yōu)化模型，如圖4所示。

圖4 變截面復(fù)合梁

考慮到懸臂梁受力時振動的穩(wěn)定性，把變截面的傳感器模型設(shè)置為對稱結(jié)構(gòu)。對于任意截面懸臂梁（截面如圖5所示），控制壓電材料的總面積s，通過協(xié)調(diào)梯形截面參數(shù)b0、b1、l 不變，使得壓電懸臂梁在常力F 作用下，產(chǎn)生的電荷最大，從而提高傳感器的靈敏度。引入偏轉(zhuǎn)角α。

圖5 變截面梁的俯視圖

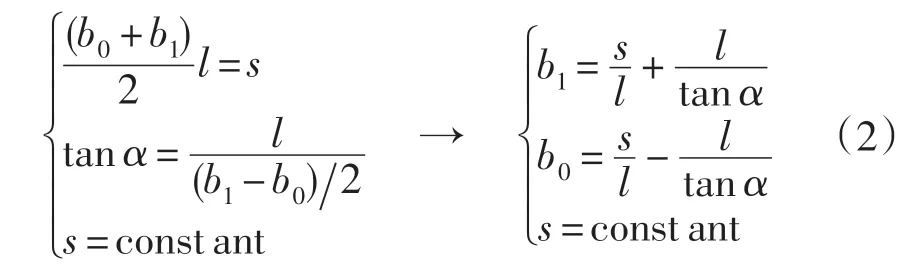
表1 為要進行懸臂梁結(jié)構(gòu)形狀優(yōu)化的初始模型參數(shù)，而要進行的優(yōu)化即為在其它條件不變的情況下，求出最佳的懸臂梁長度l，和角度α，使得在力F 的作用下，輸出電荷Q 最大。建立的優(yōu)化模型如下：

表1 壓電懸臂梁模型初始參數(shù)

2.1.1 目標函數(shù)：壓電懸臂梁力—電荷轉(zhuǎn)化關(guān)系的推導(dǎo)

對于PZT壓電材料，其壓電系數(shù)dij用矩陣表示，壓電方程為：

根據(jù)壓電懸臂梁的結(jié)構(gòu)，圖4 所示，梁的z軸方向承受作用力，對于薄膜符合材料層，可以認為梁發(fā)生純彎曲變形，忽略σ2、σ3、τ4、τ5、τ6。

公式（4）化簡為：

由公式（5）可知，只要計算出復(fù)合材料層中PZT 層中的應(yīng)力分布σ1，對公式（5）兩邊積分，即可求出在力F 作用下，傳感器產(chǎn)生的感應(yīng)電荷Q。故需先求出σ1。

在坐標為x 處，變截面懸臂梁在此處的寬度為bx，參考圖5變截面梁的俯視圖，可得出：

同時，在坐標x 處，距離中性軸的的縱向坐標為z 時，由彎曲產(chǎn)生的應(yīng)力σz：

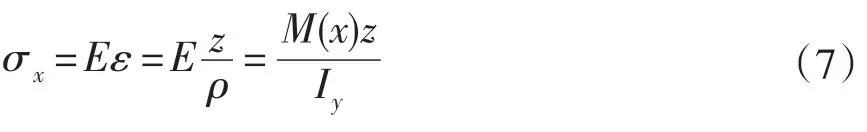
式（7）中：E 為梁的彈性模量；ρ 為梁彎曲后的曲率半徑；z 為距中性面的Z 向坐標；M（x）為距離原點x 處的力矩；Iy為此截面相對于中性軸的慣性矩。

因此，只要求出中性面的位置z0和截面相對于中性軸的慣性矩Iy，就可把公式（7）代入（4）求出截面內(nèi)的感應(yīng)電荷密度，最后通過積分即可求得在力F 作用下產(chǎn)生的電荷量Q。

根據(jù)等效截面法，把復(fù)合懸臂層各層的厚度等效為Si 的厚度，得出中性層距復(fù)合梁底層的高度為z＇：

式（8）中hi為懸臂梁各層的厚度，復(fù)合梁等效成si 梁后的等效二次慣性矩I＇：

將公式（6）、（8）、（9）帶入公式（7），可得復(fù)合懸臂梁受力F 的作用時，離原點x 處，PZT 壓電層受到的平均應(yīng)力σx，為：

將公式（10）代入壓電方程（5），并對整個具有上、下電極的壓電層進行積分，可得復(fù)合微懸臂梁受力F 的作用時，產(chǎn)生的電荷總量Q：

式（1）中：m 為引入的中間變量。

2.1.2 求解約束條件：

由于懸臂梁是純彎曲[7]，當(dāng)在自由端施加壓力F 后，在坐標x 處產(chǎn)生彎矩M（x），在截面處的應(yīng)力分布如圖6 所示，任意點的正應(yīng)力與該點到中性軸的距離成正比，即沿高度方向，正應(yīng)力按直線規(guī)律變化。

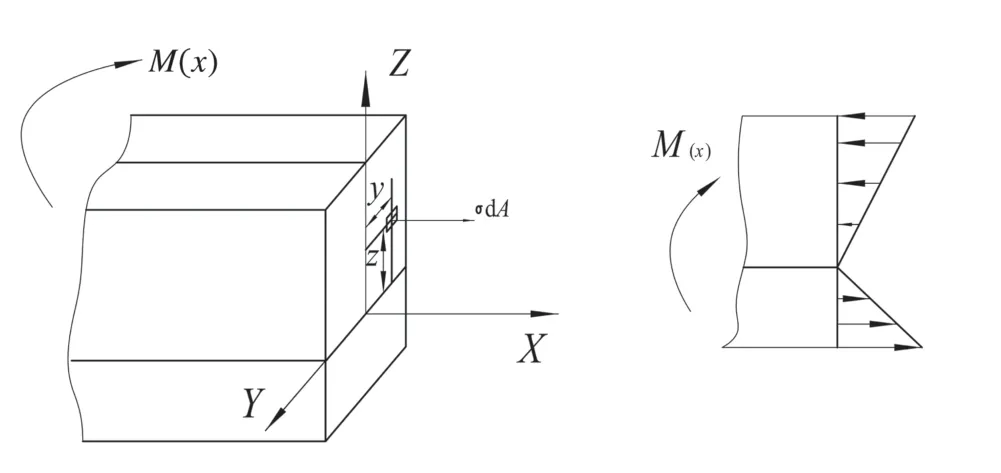
圖6 懸臂梁彎曲時的應(yīng)力分布

設(shè)各層的正應(yīng)力最大為σimax（其中i max 代表是第i 層的最大應(yīng)力，從底部算起，分別為第1層，第2 層……），由公式（6）可知，在懸臂梁固定端，產(chǎn)生的彎矩最大，同理根據(jù)圖7，在每一層薄膜最靠近懸臂梁上下端面時，產(chǎn)生的軸向應(yīng)力最大，因此，只需校核此處的應(yīng)力是否滿足許用應(yīng)力條件。

把公式（11）、（12）代入初始的優(yōu)化模型（3）得：

2.2 模型求解

本模型屬于多變量非線性規(guī)劃約束問題極大值求解，應(yīng)用自適應(yīng)懲罰函數(shù)法[8]，把約束問題轉(zhuǎn)化為非約束問題后，應(yīng)用遺傳算法求解。

圖7 遺傳算法流程

2.2.1 構(gòu)造懲罰函數(shù)

由優(yōu)化模型（17）構(gòu)造輔助函數(shù)為：

把公式中的后一項作為懲罰函數(shù)p（α、l）

其中Ki（i=1、2……5）為懲罰因子，通常取較大的值，因此模型（13）可轉(zhuǎn)化為如下問題：

為了較好的解決懲罰因子的確定問題，將懲罰因子選取為自變量（α、l）的函數(shù)，并且為了加快收斂速度，借鑒了“多級懲罰”的思想[8]——對違反約束大的段給予較大的懲罰而違反約束小的段給予較小的懲罰，按下式構(gòu)造懲罰函數(shù)：

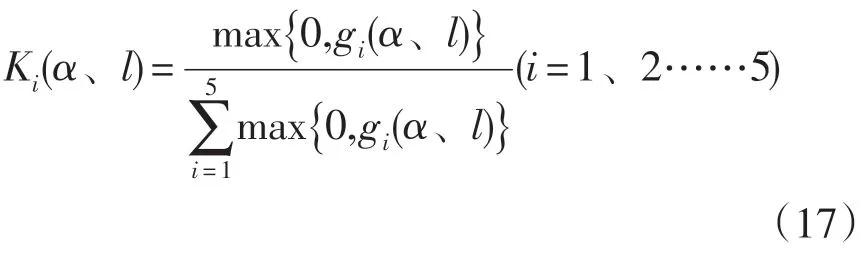
輔助函數(shù)（18）變形的：

2.2.2 基于懲罰函數(shù)法的遺傳算法

（1）參數(shù)設(shè)置

群體大小M=80，終止進化代數(shù)G=100，交叉概率pc=0.8，變異概率pm=0.1。

（2）編碼

先確定染色體二進制編碼串的長度，在matlab編程中，調(diào)用如下函數(shù)求解各變量的字符串長度：

代入公式（20），得：L=L_α+L_l=8+10=18。

（3）解碼

（4）選擇和遺傳

①選擇算子：輪盤選擇算子；②交叉算子：單點交叉；③變異算子：基本位變異。

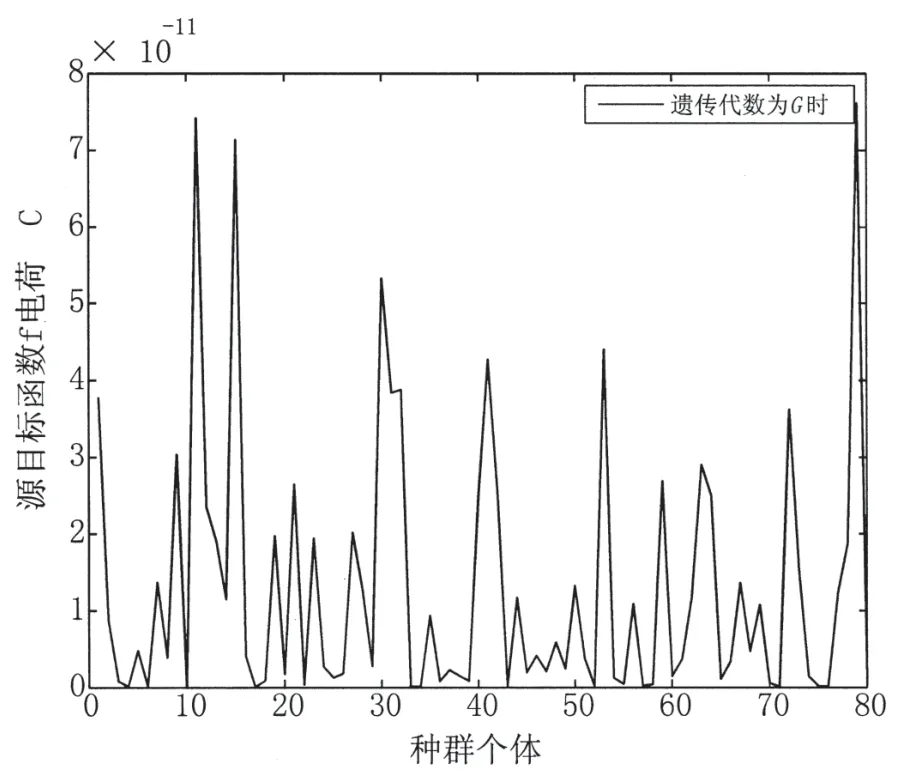
圖8 最大遺傳代數(shù)時，目標函數(shù)值得分布圖

3 結(jié)論

由遺傳算法[9]的優(yōu)化結(jié)果可知，當(dāng)l=1.13×10-3m，α=1.206，得到的感應(yīng)電荷Q1=7.485×10-11C，而在相同的壓電材料s 下，初始模型l0=1.6×10-3m，α0=π 2 時，初始感應(yīng)電荷Q0=6.693 7×10-11C，而由公式（1）得：傳感器的靈敏度與感應(yīng)電荷成正比，即優(yōu)化后的傳感器靈敏度提高了11.82%。

［1］田裕鵬，姚恩濤，李開宇.傳感器原理［M］.北京：科學(xué)出版社，2007.

［2］章吉良，周勇，戴旭涵.微傳感器［M］.上海：上海交通大學(xué)出版社，2005.

［3］格雷戈里T.A.科瓦奇.張文棟，董海峰，熊繼軍，等譯.傳感器與微執(zhí)行器全書［M］.北京：科學(xué)出版社，2003.

［4］張奇，任權(quán)，靳鵬云，等.基于微懸臂梁的傳感技術(shù)研究［J］.現(xiàn)代科學(xué)儀器，2010（2）：180-183.

［5］梁明富，趙翔.基于MEMS 技術(shù)硅微懸臂梁制作工藝研究［J］.新技術(shù)新工藝，2009（4）：27-30.

［6］黃樹森，李昕欣，王躍林，等.MEMS 傳感器性能提高相關(guān)技術(shù)研究［J］.儀器與儀表，2003，（1）：8-25.

［7］范存新.材料力學(xué)［M］.重慶：重慶大學(xué)出版社，2011.12.

［8］陳立周.機械優(yōu)化設(shè)計方法：3 版［M］.北京：冶金工業(yè)出版社，2005.

［9］雷英杰，張善文，李續(xù)武，等.MATLAB 遺傳算法工具箱及應(yīng)用［M］.西安：西安電子科技大學(xué)出版社，2005.