需求不均衡的制梁臺座規模優化算法改進研究

李艷茹,唐元寧,周國華

需求不均衡的制梁臺座規模優化算法改進研究

李艷茹1,唐元寧2,周國華2

(1.西南交通大學交通運輸與物流學院,成都610031;2.西南交通大學經濟管理學院,成都610031)

根據箱梁預制工藝的要求,模具的周轉周期T2通常為3～5 d,而文獻[1]中制梁臺座規模優化算法僅適合于模具的周轉周期T2=1 d的情況。針對文獻[1]的局限性,試圖通過作圖、試算和歸納等一系列工作,找出適用于T2=[1,T1]時計算最優制梁臺座數和模具數的通用算法,進一步擴大了算法的適用性。同時,結合文獻[1]的工程實例,利用Matlab語言編程驗證了改進算法的可行性。

預制梁場;制梁臺座;模具周轉周期;需求不均衡;

預制梁是大型橋梁工程和高速鐵路橋梁建設工程不可缺少的重要構件之一,它往往在預制梁場進行生產,其生產能力受預制梁場的制梁臺座數約束,而生產能力又直接影響整個建設工程的工期[1-2],故制梁臺座的規模優化對預制梁場的合理規劃和設計具有重要意義,間接對整個高速鐵路建設工程產生一定的影響。我國現階段預制梁場的制梁臺座規模的確定,大多是根據技術人員多年的工程施工經驗來確定,人為因素較大,常常會因為缺少計劃被迫對實施方案進行臨時調整,從而造成施工管理混亂或資源浪費,嚴重影響工程進度并增加工程成本[3-5]。也有些確定方法具有理論依據,但考慮因素較為單一,很多文章只考慮了架梁需求均衡的情況或是只考慮了制梁臺座數量,而忽視模具的數量[7-12]。即使文獻[1]綜合考慮到以上眾多因素,探討了需求不均衡的預制梁場制梁臺座規模和模具數量的確定方法,但此方法僅適合于模具的周轉周期T2=1 d的情況。而事實上,根據箱梁預制工藝的要求,模具的周轉周期T2通常為3～5 d,此時文獻[1]的方法不再適用。因此,針對文獻[1]的局限性,本文通過作圖、試算和歸納等一系列工作,找出了適用于T2=[1, T1]時計算最優制梁臺座數和模具數的通用算法,進一步擴大了算法的適用性。同時,結合文獻[1]的工程實例,利用Matlab語言編程驗證了改進算法的可行性。

1 制梁臺座規模的原優化算法

1.1 問題描述及特點分析

某預制梁場承擔了某橋梁工程預制箱梁的生產任務,其中箱梁總需求數為D榀,架梁總工期為T(d),分成n次架梁作業,第i次架設的梁數量為di,第i次架梁作業和第i-1次架梁作業的時間間隔為ti。設單榀箱梁完成整個預制工序所需時間為T1,模具的周轉周期T2= 1 d,要求在滿足架梁進度前提下,確定最優的預制梁臺座和模具的數量,以節約生產用地及建設成本[1,6]。

該問題具有以下幾個特點[1]:

(1)n次架梁作業可看作n個階段的生產作業,第i次架設箱梁數就是第i階段的箱梁需求量,第i階段的時長為ti;

(2)第i階段的需求量di來自于第i階段生產出來的成品箱梁數量;

(3)第i階段生產出來的成品箱梁數量不僅來源于本階段的產量,也來源于第i-1階段的在制梁及成品梁數量。

1.2 最小的制梁臺座數計算

最小制梁臺座數量的計算和模具數量的計算可參考文獻[1]給出的計算模型和計算過程,并以工程實例來驗證:當T2=1 d時,該算法相較于傳統算法具有一定的優勢且是可行的。

1.3 原優化算法的局限性

文獻[1]只考慮了T2=1 d的情況,那么,當T2＞1 d時呢?根據文獻[1],可以把確定模具數量的公式g=ceiling(q/T1,1)中的數據1用字母T2來代替(因為已知T2=1 d),此時,g的算法有以下2種可能的推測。

(1)推測一

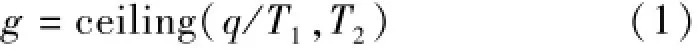
式中,ceiling(number,significance)函數表示將參數number向上舍入(沿絕對值增大的方向)為最接近的significance的倍數;g為模具數;q為制梁臺座數; T1為箱梁預制周期;T2為模具周轉周期。

這一推測不具有可行性,這里以具體數據來說明。假設,當q=24,T1=8,T2=3,由推測一計算得g= ceiling(q/T1,T2)=3。此時制梁臺座沒有被充分利用,可以從兩方面進行解釋:①和文獻[1]計算結果相比,q和T2都有所增大,為了使制梁臺座充分利用,相應地,模具數量g也應增大。但是,從計算結果來看,g仍為3,故制梁臺座沒有被充分利用;②制梁臺座數對制梁速率的影響是q/T1=24/8=3,即每天制梁數量為3榀,模具數對制梁速率的影響是g/T2=3/3=1,即每天制梁數量為1榀。可見,模具數不足成了制梁效率的瓶頸,在該模具數下,制梁臺座被閑置,未充分利用。

(2)推測二

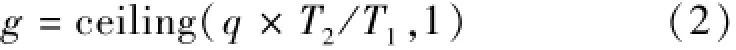
式(2)中參數同推測一。

為了使制梁臺座在一個周期內盡可能不閑置,必須有制梁臺座數對制梁速率的影響不大于模具數對制梁速率的影響,即有q/T1≤g/T2,從而得到g≥q× T2/T1,所以最小的模具數g=ceiling(q×T2/T1,1)。

推測二可以有效使得制梁臺座在一個周期內盡可能不閑置,但在這種情況下,文獻[1]中vk的計算方法又不具可行性了,下面仍以文獻[1]中的算法來進行驗證。

將推測二g的計算方法應用到文獻[1]中的例子(僅有一點不同的是T2=3 d),其他步驟和文獻[1]相同,此時可求得q=18,g=7。按照文獻[1]中vk的計算方法,前2 d每天可生產箱梁7榀,2 d共可生產箱梁14榀。而實際上,由于T2=3,第1天生產7榀箱梁是可以的,而第2天雖然有閑置制梁臺座,但是沒有閑置的模具,生產的箱梁為0榀,那么2 d共生產箱梁為7榀,這與文獻[1]不符,可見文獻[1]中vk的計算方法是行不通的。綜上所述,文獻[1]中vk的計算方法只適用于T2=1 d的情況,由于模具周期為1,使得模具每天都有閑置,且閑置數目都是7,所以只要制梁臺座有閑置就可以制梁。但是當T2＞1 d,就必須考慮模具是否空閑。

2 制梁臺座規模優化算法的改進

2.1 最小的制梁臺座數計算

在改進算法中,問題的描述和特點分析同原優化算法一致,所不同的是,改進算法中假設模具的周轉周期T2可以取[1,T1]的任何值。由于模具周轉周期可以不為1 d,導致了文獻[1]中確定g、m和vk的計算方法不再適用。其中,原文的計算方法如下。

(1)模具數量的計算:g=ceiling(q/T1,1)(前文已證明);

(2)模具與制梁臺座的匹配關系m值的計算:①若m=int(q/g)≠q/g,根據e=q mod g,則e套模具每套對應m+1個制梁臺座,g-e套模具每套對應m個制梁臺座進行生產。②若m=int(q/g)=q/g,則每套模具對應m個制梁臺座進行生產,此時e=0;

(3)k子過程第ck周期開始的第jk天內能產出成品梁數的計算

相關參數的含義見文獻[1]。

通過作圖、試算和驗證發現,以上確定g、m和vk的計算方法不適用于T2＞1 d的情況,故本文的改進算法是基于文獻[1]的計算方法,通過改進g、m和vk三個參數的計算方法,使得新算法更具普適性。

具體改進計算如下。

(1)模具數量g的確定

由推測二可得,為使模具在一個周期內盡量不閑置,則相應的模具數g為

g=ceiling(q·T/T,1)=ceil(q·T/T)(3)

式(3)中ceil函數表示向上取整,其他參數含義同推測一。

(2)模具與制梁臺座的匹配關系m,n值的確定

在一個模具周轉周期T2內,前m天每天產出的成品梁數目為ceil(g/T2)-1,后n天每天產出的成品梁數目為ceil(g/T2),該時段內產出的成品梁數目受模具數的制約,即有m,n滿足的關系式如下

解得

(3)vk的確定

k子過程第ck周期開始的第jk天這一天能產出成品梁數量uk為

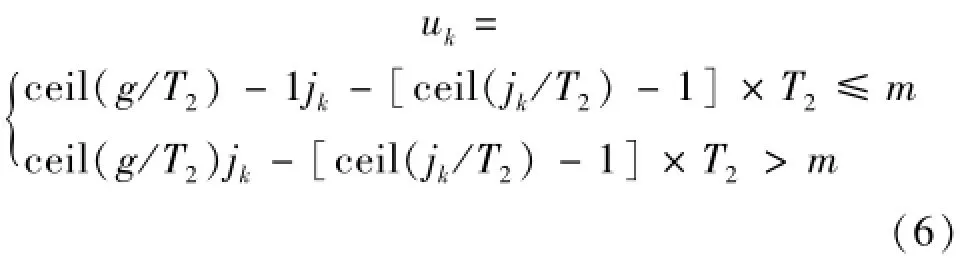
式(6)中,jk天內模具周轉ceil(jk/T2)-1次后剩余天數不大于m時,每天的成品梁數目為ceil(g/ T2)-1,否則為ceil(g/T2)。

k子過程第ck周期開始的jk天內能產出成品梁數量vk為

式中,vk為1～jk天每天產出的成品梁數目累計之和。

(4)除以上3個參數的計算有所改進,其他參數(如ck、jk等)的計算方法不變,仍參照文獻[1]。

2.2 案例驗證

本文擬引用文獻[1]的工程實例進行改進算法的驗證,即某架梁工程需要成品箱梁320榀,制梁總工期為150 d,分5次架梁作業,每次架梁需求及相鄰架梁時間間隔見表1。

表1 成品箱梁需求

基于以上工程實例的已知條件,分別求解T1= 8 d,T2=[1,T1]時,相匹配地最優制梁臺座數和最優模具數量。本文利用Matlab語言實現改進算法的計算過程,求解見表2。

表2 T1=8 d,T2=[1,T1]時的q、g

從表2可以看出,當T2=1 d時運行程序得q=19, g=3,和文獻[1]的計算結果相同,這表明改進后的算法是包含文獻[1]中T2=1 d的情況。另外,隨著模具周轉周期T2的增加,需要的模具數量也隨之增多,甚至當T2增加一定數值后還會引起制梁臺座數量的增多,這表明模具周轉周期T2極大地影響著模具數量g,同時對制梁臺座數量q也有一定的影響。最后,當模具的周轉周期T2增加到與制梁周期T1一致時,此時需要的模具數量g就與制梁臺數量q一樣多,才能滿足生產要求。

3 結論

針對文獻[1]的局限性,對文獻[1]中g、m和vk的計算方法進行了有效改進,提出適用于T2=[1, T1]時計算最優制梁臺座和模具數量的通用算法,較文獻[1]更具適用性;而且通過工程實例的應用,表明了模具周轉周期T2的取值直接影響著制梁臺座的數量。當然,影響制梁臺座規模的控制性因素有很多,除了本文所述的模具周轉周期、模具數量、箱梁預制周期等,還與架梁速率、存梁臺座規模、搬移梁設備的工效、天氣氣候、混凝土原材料及配合比、養護方式、混凝土強度增長速度等密切相關。今后研究的方向,可考慮更多的控制因素綜合作用下制梁臺座的規模優化問題。

[1] 方必和,徐慶.需求不均衡的預制梁場梁臺規模優化算法研究[J].工程與建設,2008(3):298- 300.

[2] 黃龍華,劉杰文.東海跨海大橋大型構件預制場及設施布置的技術特點[J].交通科技,2004(1):7- 9.

[3] 甄寶山.現場制梁預制場選擇與布置[J].鐵道建筑技術,2000 (5):27- 29.

[4] 梁志堅.預應力混凝土空心板梁的預制施工技術[J].工程建設與設計,2006(3):61- 63.

[5] 黃建陽.大規模T型梁現場預制施工與管理[J].中國港灣建設, 2004(2):39- 45.

[6] 徐慶.大型橋梁工程預制梁場設計及生產優化研究[D].合肥:合肥工業大學,2008:31- 33.

[7] 紅軍,曹新岡.高速鐵路大噸位箱梁預制場的規劃與設計[J].建材技術與應用,2009(1):30- 32.

[8] 葛敏.武廣鐵路客運專線制梁場設置方案[J].鐵道標準設計, 2010(1):116- 117.

[9] 姜麗雯.鐵路客運專線預制梁場的規劃設計研究[J].鐵道標準設計,2007(6):8- 12.

[10]薛寧鴻,張文格.高速鐵路客運專線預制梁場規劃建設及施工管理綜述[J].鐵道標準設計,2010(S1):85- 88.

[11]李寶濤.淺談鐵路客運專線梁場規劃設計與優化[J].科技情報開發與經濟,2011(21):189- 192.

[12]李利方.武廣鐵路客運專線預制箱梁梁場建設規模的研究[J].鐵道建筑,2010(1):84- 86.

Study on Im proved Optim ization A lgorithm for the Scale of Girder-fabrication Bed in Uneven Demand

LIYan-ru1,TANG Yuan-ning1,ZHOU Guo-hua2
(1.School of Transportation and Logistics,Southwest Jiaotong University,Chengdu 610031,China; 2.School of Econom ics and Management,Southwest Jiaotong University,Chengdu 610031,China)

According to the requirements of box girder prefabrication process,the turnover cycle ofmold is usually 3～5 days,but the optimization algorithm for the scale of girder-fabrication bed in the literature[1]is only suitable for thosemodeswith turnover cycle of1 day.So,contrary to the limitations of the literature[1],after a series ofwork includingmapping,calculating,generalizing,this paper proposes universal algorithm for computing the optimal number of the girder-fabrication bed and itsmold when the turnover cycle is the any integer at the interval1 and T1,so as to further expand the applicability of the algorithm.Simultaneously,in combination with those project examples in literature[1],the feasibility of this improved algorithm is verified by Matlab programming.

girder-prefabrication yard;girder-fabrication bed;turnover cycle ofmold;uneven demand

U445.47

A

1004- 2954(2013)07- 0054- 03

2012- 12- 13;

2013- 01- 05

鐵道部科技研究開發計劃重點課題(2011G010-D);中央高校基本科研業務費專題項目(SWJTU12ZT12)

李艷茹(1987—),女,碩士研究生,E-mail:liyanru102@ 126.com。