電調諧式微帶線濾波器的設計

任鎳，張澤宇

（武漢船用電力推進裝置研究所，武漢 430064）

0 引言

隨著高速信號處理技術的發展，濾波器作為最基本的信號處理元件之一在各種控制系統中起著非常重要的作用。電調諧濾波器由于其中心頻率可變、調諧方式靈活、構成方式多樣等優點受到越來越多的關注，本文在電調諧濾波器原理的基礎上[1]，研究了微帶線外部耦合系數及級間耦合系數對電調諧式濾波器的影響，并基于提取參數法設計出了一種調諧范圍寬、插損小的電調諧濾波器。

1 抽頭式電調諧濾波器設計

本文基于濾波器設計的提取參數法[2]，它適用于各種不同的耦合濾波器物理結構。濾波器等效電路如下圖1、圖2所示。

由圖1、圖2可知，假定各諧振器的諧振頻率ω，諧振器間耦合系數Mij，影響濾波器響應特性的主要參數就是：輸入輸出端口阻抗RL和RC。結合等效模型，抽頭式梳狀線濾波器端口阻抗RL和RC的大小取決于抽頭線的位置，諧振頻率ω取決于加載電容的大小，級間耦合系數Mij則取決于耦合微帶線的線間距。

圖1 n階耦合諧振器的等效電路

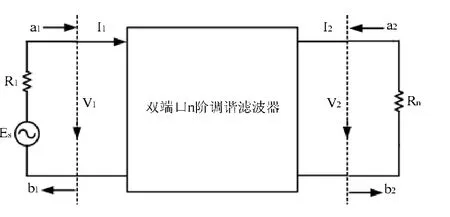
圖2 n階耦合諧振器的雙端口等效圖

可以利用耦合結構設計法[4]來確定梳狀線濾波器的物理尺寸參數。梳狀線濾波器設計參數如下[5]。設定濾波器相對帶寬值FBW為4%，低通原型的歸一化值根據性能指標設定為g0=1、g1=0.8430、g2=0.6220、g3=0.6220。

那么濾波器外部品質因數：

耦合系數：

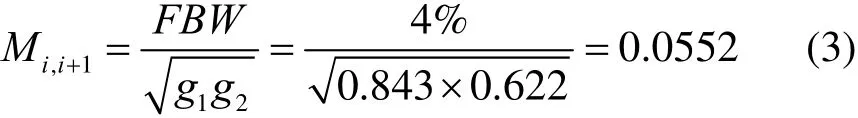
其中，i為濾波器的級數，Qe1和Qen為輸入輸出諧振器的外部品質因數，Mi,i+1為相鄰諧振器間的耦合系數。

2 設計仿真

2.1 外部耦合系數和級間耦合系數的仿真

Ansoft HFSS是一種基于有限元方法的三維結構電磁場仿真軟件，具備任意三維無源結構的全波電磁場分析求解能力以及強大的數據處理能力。本文在Ansoft HFSS中建立梳狀線濾波器單端口三維模型和梳狀線濾波器級間耦合三維模型，如圖3和4所示。

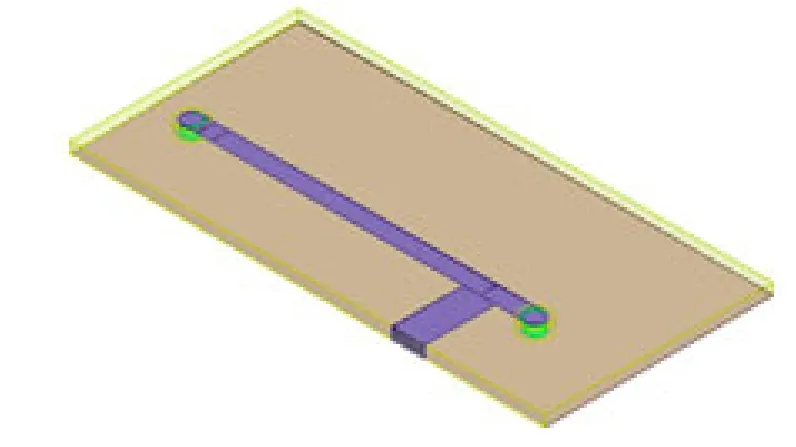
圖3 梳狀線濾波器單端口三維模型

通過仿真計算，可以得出外部耦合系數與抽頭對地距離的關系曲線，從而確定抽頭對地距離為3.3 mm，通過級間耦合系數與微帶線間距關系曲線從而確定微帶線間距3.4 mm。

2.2 濾波器整體電路聯合仿真

本文通過在 Agilent公司開發的 ADS（Advanced Design System）軟件仿真版圖和電路聯合模型，抽頭線梳狀線濾波器模型如圖5所示。

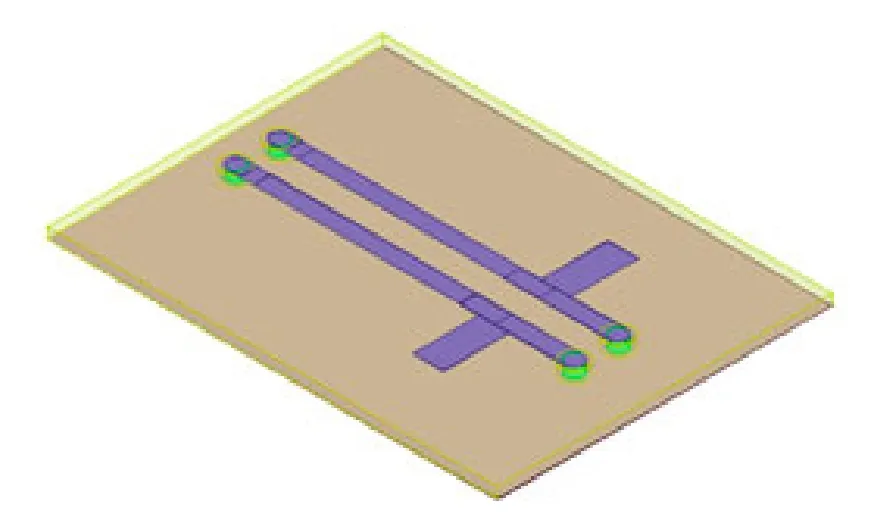
圖4 梳狀線濾波器級間耦合三維模型

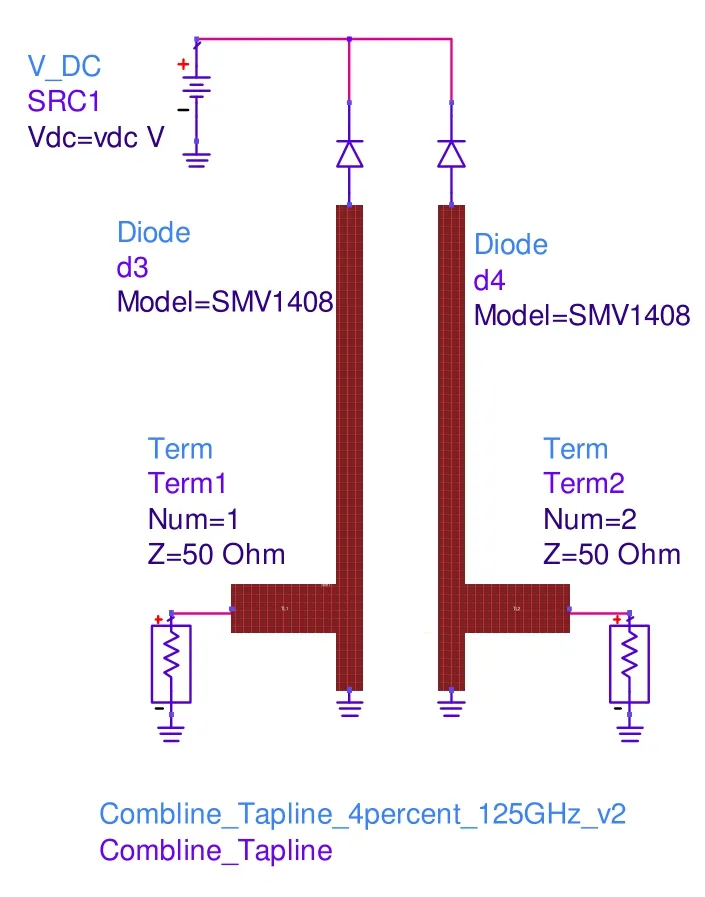
圖5 梳狀線濾波器模型

再對其進行仿真優化后，得出了梳狀線濾波器的參數曲線，如圖6所示。

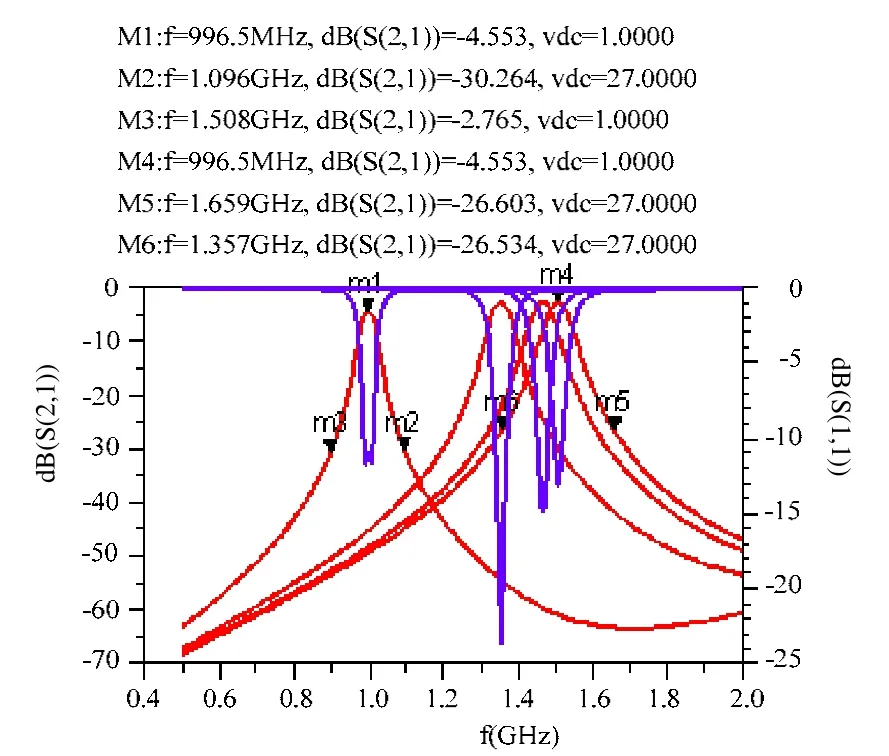
圖6 入實際模型后的梳狀線濾波器的仿真曲線

結合圖6可得，電調諧濾波器的頻率調諧范圍為0.997~1.503 GHz，符合本文所預期的頻段；插入損耗最大為4.554 dB，符合IL<5 dB的要求；相對帶寬為4.1%~4.2%，略大于4%；端口駐波比<2；帶外抑制>25 dB，滿足項目設計的需要。

需要注意的幾點是，濾波器的插損隨頻率的變化而變化，主要是由于等效串聯電阻的影響。濾波器的低頻端回波損耗特性并不是很好，這是由于在設計時所需用的是中心頻率為1.25 GHz的帶通濾波器，因此諧振器的長度和抽頭對地距離以及耦合間距都是固定不變的 ，而抽頭位置決定外部耦合，因此在低頻端呈現過耦合狀態，在高頻端呈現欠耦合狀態。

3 結束語

通過提取參數法對濾波器模型進行了仿真設計，設計出了1~1.5 GHz 的電調諧梳狀線濾波器。仿真結果顯示此濾波器電調諧頻率范圍寬、結構簡單體積小巧、插入損耗低。設計過程發現品質因數更高的等效串聯電阻可以減小濾波器的插入損耗，改進電調諧微帶線濾波器低頻和高頻下的駐波系數，同時通過改進等效串聯電阻的偏置電路可以減小偏置電路對濾波器帶寬的影響。

[1] 李曉陸. 短波頻率管理技術[J]. 艦船電子技術,2003, (5), 53-55.

[2] Penalva G. T., Risueno G. L., Alonso J. I. A simple method to design wide-band electronically tunable combline filters[J]. IEEE Trans, 2002, (50): 172-177.

[3] Jia-Sheng Hong. Microstrip Filters for RF/Microwave Applications[J]. New York: John Wiley&Sons, 2001,(10): 12-15.

[4] Matthaei G. Comb-line band-pass filters of narrow or moderate bandwidth [J]. The Microwave Journa1,1993(1): 35-38.

[5] Thomas A. Dimensions of microstrip coupled lines and interdigital structures [J]. IEEE Transaction on Microwave Theory and Techniques, 1977: 405-410.