城市隧道口交通優(yōu)化方案研究
徐曉丹,林 麗
(南京林業(yè)大學(xué)汽車與交通工程學(xué)院,南京210037)
城市隧道使城市道路交通形成立體交通模式,消除了城市道路交叉口車流、人流的相互影響,減少了地面車流的干擾,使交通流能夠快速地通過路段,減少了道路的占用時間。我國的相關(guān)設(shè)計規(guī)范[1]規(guī)定了隧道出口與平面交叉口的距離要滿足具體的設(shè)計要求,但是由于城市地下道路構(gòu)造上的特點(diǎn),決定了其交通受限于出入口,幾乎所有的城市隧道都不同程度地存在著出入口交通瓶頸問題[2]。嚴(yán)重時造成城市隧道及其周邊道路交通阻塞,影響了道路的通行能力。目前,城市隧道出口的對外銜接組織形式有多種,本文選用的“隧道+地面”形式主要是車輛駛出城市隧道出口后在較短距離內(nèi),立即進(jìn)入信號交叉口區(qū)域的這樣一種情況,具體組織形式如圖1所示。在此基礎(chǔ)上,分析觀測數(shù)據(jù)與通行能力計算結(jié)果,形成城市隧道出口銜接路段長度模型,并結(jié)合實(shí)例仿真驗(yàn)證。隧道出口銜接路段的合理設(shè)置,有利于提高銜接路段的通行能力,便于交通組織和交通管理,同時對于提高行車安全也具有重要意義。
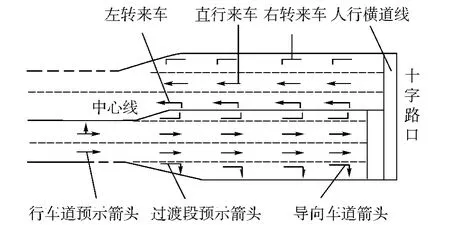
圖1 出入口與十字型路口銜接[3]Fig.1 The entrance and exit link up with intersection
1 城市隧道出口安全距離的確定
1.1 城市隧道出口安全距離的影響因素
將隧道出口段滿足車輛安全行駛所需的距離定義為隧道出口安全距離 (簡稱L安)。影響安全距離的因素有很多,但是根據(jù)研究表明,駕駛員在駕駛過程中接收的所有信息中,憑借瞳孔所獲取的占80%~90%,所以駕駛員的瞳孔是獲取外界信息的主要方式,由于駕駛員受到隧道進(jìn)出口明暗適應(yīng)的影響,其駕駛行為存在一定的危險性;另外,隧道出口線形直接會使車輛產(chǎn)生加速或減速。
(1)駕駛?cè)艘曈X適應(yīng)能力分析。首先定義駕駛?cè)斯膺m應(yīng)過程中的瞬時盲期現(xiàn)象為視覺震蕩。通過瞳孔面積最大瞬態(tài)速度值 (MTPA)指標(biāo),將瞳孔面積變化速度及換算視覺震蕩持續(xù)時間結(jié)合,能合理解釋隧道進(jìn)出口路段視覺負(fù)荷。
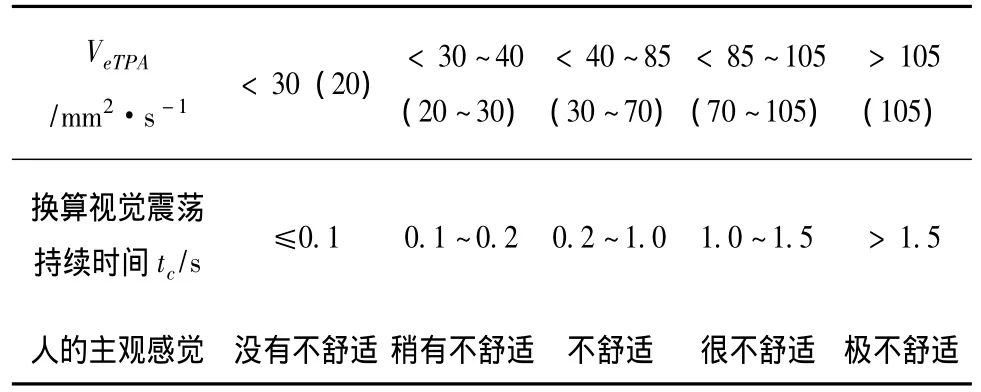
表1 VeTPA與視覺舒適度關(guān)系[4]Tab.1 Relationship between VeTPAand visual comfort degree of tunnel entrance and exit

表2 隧道進(jìn)出口行車試驗(yàn)換算視覺震蕩持續(xù)時間Tab.2 Conversion duration for visual turbulence of tunnel entrance and exit by driving experiment
綜合考慮城市隧道的限制條件,結(jié)合道路通行能力及車速限制等城市道路環(huán)境的安全因素,主要考慮了城市隧道出口視覺震蕩對行車安全的影響。由表1、表2可知,當(dāng)換算視覺震蕩持續(xù)時間大于1.5 s時,駕駛員的主觀感覺為極不舒適;城市隧道出口的一般限速V為40~60 km/h,根據(jù)L安=V×tc,當(dāng)tc取1.5 s時,算出的隧道出口安全距離為17~25 m,所以為了保證安全,取換算視覺震蕩持續(xù)時間tc為2 s,得到隧道出口安全距離公式L安=2V,V為隧道出口的設(shè)計車速(規(guī)定的最大行駛車速,暫不考慮線形產(chǎn)生的加速度)。

圖2 出口加速度與線形危險度關(guān)系[7]Fig.2 Relationship between the export acceleration and the alignment risk degree
(2)道路線形的影響分析。在不同的道路交通環(huán)境下,道路線形對車輛的行駛速度有較大影響,且不同的線形指標(biāo)對車速的影響程度也不一樣。為綜合反映道路線形與車速變化的關(guān)系,引入線形危險度的概念[5]。隧道出口加速度與線形危險度的關(guān)系如圖2所示。
可能受到道路條件和照明條件的影響,加速度與線形危險度有一定的離散性,但是仍可以得出結(jié)論:出口線形危險度越大(線形越差),其加速度值越大,即車速變化越大,行車越不安全。當(dāng)車輛駛出隧道時,駕駛?cè)藭鶕?jù)前方線形采取駕駛操作,當(dāng)線形較好時會采用較大的加速行為,當(dāng)線形差時會采用較小的加速行為,甚至?xí)p速,這時隧道出口外與隧道出口處存在車速差[6]。
1.2 隧道出口車速的變化
駕駛?cè)诵睦硇袨椤缀尉€形和道路環(huán)境等多方面要素最終都以車輛運(yùn)行速度的形式反映出來。因此,本文將車速作為建立隧道出口道路線形、駕駛?cè)艘曈X影響和道路交通安全的“橋梁”。當(dāng)車速有較大落差時,往往會使駕駛?cè)舜胧植患埃瑢?dǎo)致行車事故,而這種速度的不連續(xù)一般是由于線形突變所致。車速的變化影響安全距離的變化,道路線形和駕駛員的視覺震蕩現(xiàn)象都是以車速變化的方式體現(xiàn),本文在建立隧道出口安全距離模型中,將車速作為重要參量。
1.3 安全距離分析與確定
受到視覺震蕩的影響,假設(shè)駕駛員在這段時間內(nèi)不采取任何駕駛操作,則車輛在隧道出口的坡道上減速,其加速度值與隧道坡度i有關(guān),即得隧道出口安全長度L安公式:
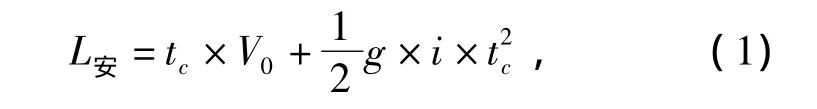
式中:tc為視覺震蕩持續(xù)時間,取2 s;V0為車輛剛出隧道時的初速度 (取隧道出口設(shè)計車速),m/s;g為重力加速度,取9.8 m/s2;i為計算范圍內(nèi)的平均坡度。
城市隧道出口與相鄰交叉口之間的銜接段長度比高速公路隧道出口銜接段長度短很多,城市隧道出口的最大縱坡不超過6%[8],在視覺震蕩期間,根據(jù)公式 (1)中的第二項(xiàng),可知0.5×9.8×6%×22=1.176 m,值較小,出口縱坡對車速的影響程度可以考慮不計,因此公式1可調(diào)整為:

在公式 (2)中,2 s為視覺震蕩持續(xù)時間(tc)。由此,可以明顯看出,影響隧道出口安全距離的因素最終用車輛行駛速度來體現(xiàn)。
2 交叉口排隊長度的確定
信號交叉口制約了城市主干路的通行能力,由于信號交叉口的通行能力低于路段通行能力,交通量稍微過大就會誘發(fā)交通擁擠,導(dǎo)致車輛在交叉口排隊。信號交叉口的排隊長度,能反映交叉口車流的運(yùn)行情況,它對評價交叉口的運(yùn)行效率、現(xiàn)狀信號配時方案的優(yōu)劣等都有重要意義。
2.1 排隊長度模型選取
本文選定SIGNAL94的優(yōu)化模型[9-12]作為基本框架,該模型只有離散系數(shù)需要標(biāo)定,模型精度高,且利用現(xiàn)有觀測的數(shù)據(jù)可以很好地對模型參數(shù)進(jìn)行修正。通過分析其在實(shí)際交通流變化情況下的實(shí)用性,建立符合信號交叉口交通流特性的排隊長度優(yōu)化模型。
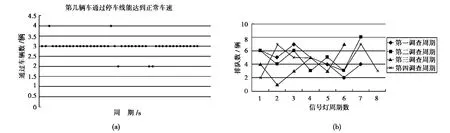
圖3 各信號燈周期排隊車輛數(shù)Fig.3 Length of queues in the each signal cycle
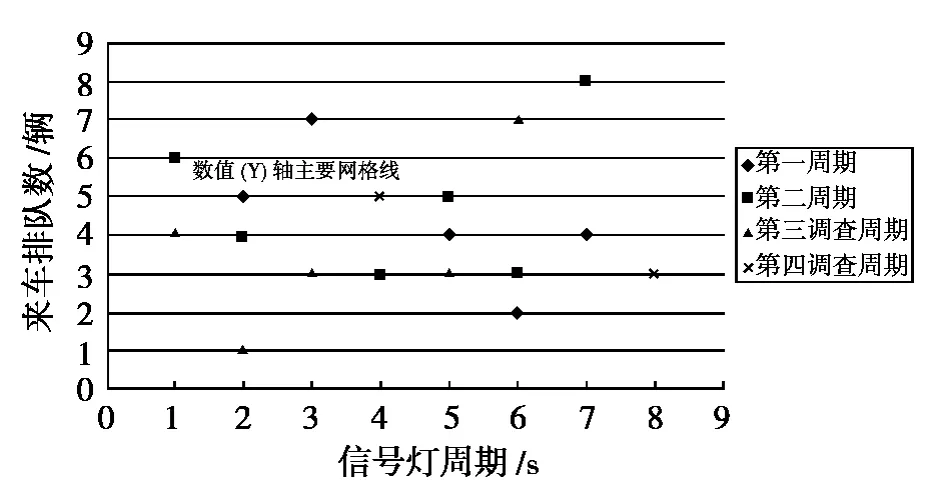
圖4 來車排隊分布散點(diǎn)圖Fig.4 Scatter diagram of queuing vehicles
模型中最關(guān)鍵的是確定路口飽和流率和確定車輛到達(dá)率。飽和流率是指當(dāng)交叉口有相當(dāng)長的車輛排隊等待時,有效綠燈時間內(nèi)通過的最大小時車輛流率。車輛到達(dá)率是指單位時間內(nèi)到達(dá)交叉口的車輛數(shù)。經(jīng)優(yōu)化后的SIGNAL94公式模型:
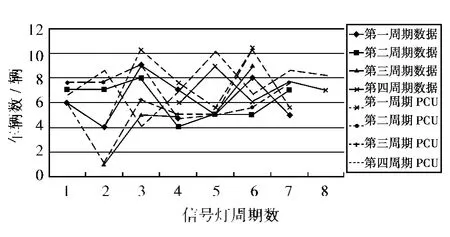
圖5 各信號燈周期放行車輛數(shù)Fig.5 Vehicles in green light period
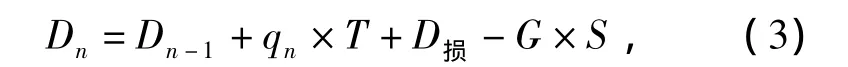
式中:Dn為第n周期的最大排隊長度,輛;Dn-1為第n-1周期滯留下來的車輛數(shù),輛(無二次排隊,Dn-1=0);qn為第n周期的車輛到達(dá)流率,輛/s;T為信號燈周期的長度,s;G為綠燈時長,s;S為飽和流率,輛/s;D損為啟動損失時間通過的車輛數(shù),輛。
其中,T、G是通過實(shí)際觀測;D損是通過數(shù)據(jù)后,繪制散點(diǎn)圖如圖3所示;qn、S是通過實(shí)測后擴(kuò)樣得到如圖4和圖5所示。對調(diào)查數(shù)據(jù)進(jìn)行處理后得出,在交叉口有效綠燈時間里,根據(jù)連續(xù)5 s以上車流通過的車輛到達(dá)數(shù),可以計算出飽和流率與車輛到達(dá)率。得到車輛到達(dá)率的統(tǒng)計分布如圖6所示。
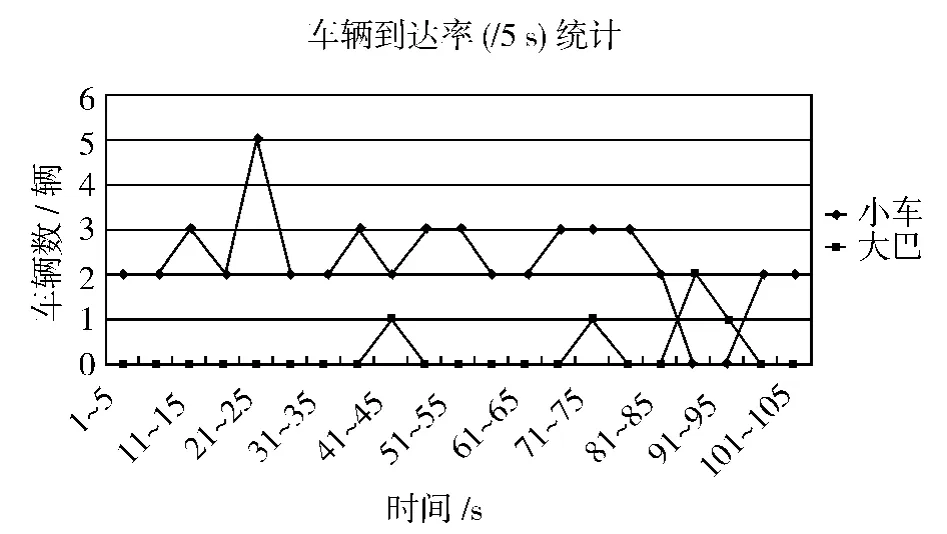
圖6 車輛到達(dá)率統(tǒng)計Fig.6 Statistical graph of approach flow rate
2.2 交叉口排隊長度的確定
由于排隊長度L排隊=Dn×L間(車頭間距),Dn根據(jù)公式 (3)得出,由此,交叉口排隊長度公式為:

在本次研究中,車輛能在交叉口功能區(qū)順暢通行的評判標(biāo)準(zhǔn)為不發(fā)生二次排隊。根據(jù)對采集的玄武湖隧道出口車輛到達(dá)率、交叉口信號配時等相關(guān)數(shù)據(jù)的分析,建立了交叉口排隊長度模型。
3 隧道出口銜接段長度模型確定
3.1 城市隧道出口銜接段長度定義
城市隧道出口銜接段長度由隧道出口安全距離和交叉口通行能力兩者共同影響確定,因此定義城市隧道出口(洞口開始)與交叉口停車線之間的這段距離為城市隧道出口銜接段長度,簡稱L銜接。
3.2 銜接段長度模型建立
通過前兩部分的研究,發(fā)現(xiàn)對城市隧道出口安全距離及交叉口排隊長度起主要影響作用的是車速和車輛到達(dá)率兩個因素,綜合考慮,優(yōu)化整合成如下模型:式中:a為調(diào)節(jié)交叉口車輛到達(dá)率對模型的影響程度;b為調(diào)節(jié)隧道出口車輛速度對模型的影響程度。
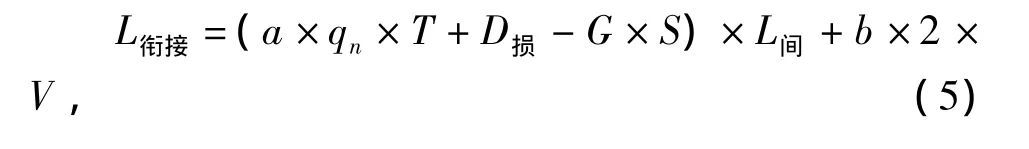
通過MATLAB對數(shù)據(jù)進(jìn)行處理,可以分析得出系數(shù)a與b之間關(guān)系圖像如圖7所示。
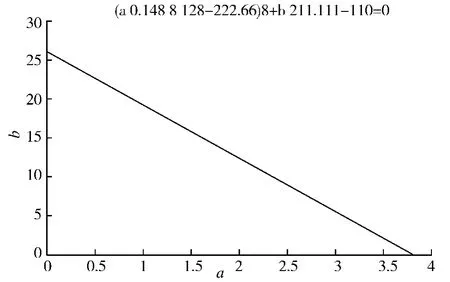
圖7 銜接長度符合要求時的a、b關(guān)系圖Fig.7 Relation graph of a and b when the connected-link meet the requirement
根據(jù)玄武湖隧道出口銜接的中央路—新模范馬路交叉口實(shí)測數(shù)據(jù),實(shí)際分別計算的兩段長度L安與L排隊之和是小于100 m的。根據(jù)分析結(jié)果,L銜接為100 m、110 m、120 m時,a、b線性相關(guān)且斜率相等,即:

在交叉路口流率、信號燈配時與隧道設(shè)計速度一定時,b≥1時,a>1(如圖7所示),這時長度滿足所研究的通暢與安全的要求,無需改進(jìn);當(dāng)b<1,a≥1時,說明隧道出口安全距離實(shí)際值小于理論值,則要適當(dāng)降低隧道設(shè)計車速以保證行車安全;當(dāng)b≥1,a<1時,說明交叉口排隊長度不滿足理論要求,則要對信號燈進(jìn)行配時優(yōu)化。
綜上所述,隧道出口處距交叉口停車線的實(shí)際長度L實(shí)際小于理論值L理論時 (L實(shí)際<L理論),根據(jù)公式 (5)對信號燈配時以及隧道設(shè)計車速進(jìn)行調(diào)整,使其滿足要求。
4 驗(yàn)證可靠度
4.1 建立仿真
針對提出的長度計算模型,借助VISSIM進(jìn)行交叉口交通流仿真。具體以鼓樓隧道出口為例,該隧道出口與玄武湖隧道出口的組織形式相似,在很短距離內(nèi)直接與中央路-傅厚崗交叉口銜接,工作日高峰時期經(jīng)常出現(xiàn)嚴(yán)重的排隊現(xiàn)象。以隧道出口實(shí)測的現(xiàn)狀交通量數(shù)據(jù)為基礎(chǔ),建立仿真模型,得到現(xiàn)狀仿真效果如圖8所示。

圖8 隧道出口銜接相鄰交叉口Fig.8 Situation of the exit of urban connecting the nearest intersection
4.2 檢測數(shù)據(jù)輸出
現(xiàn)狀排隊長度與改善后排長度檢測數(shù)據(jù)見表3和表4。
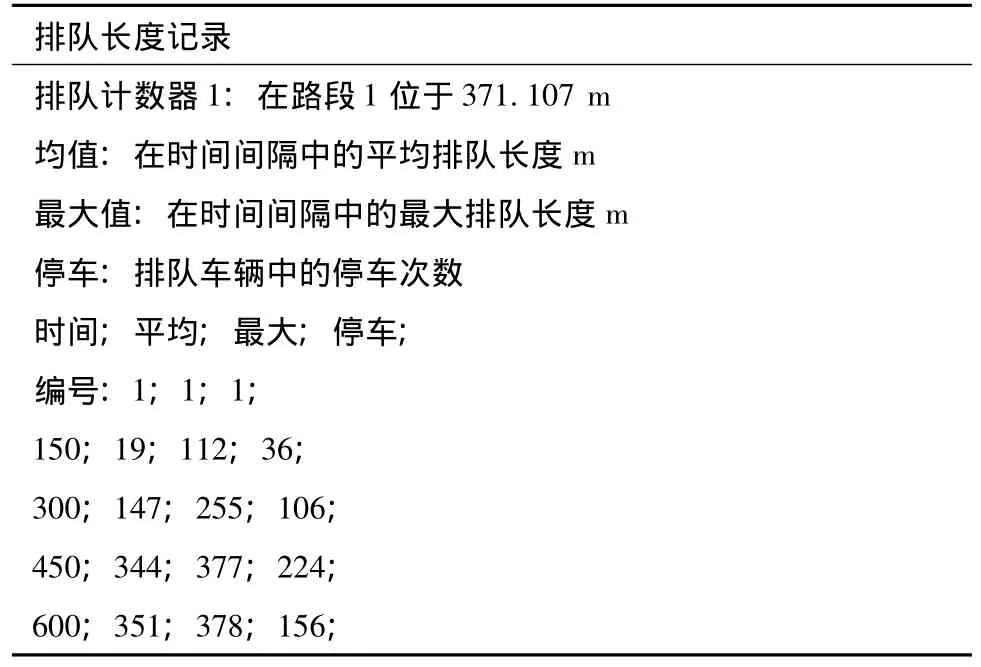
表3 現(xiàn)狀排隊長度檢測數(shù)據(jù)輸出表Tab.3 Output of the detected queues at present
4.3 仿真結(jié)果分析
VISSIM的排隊計數(shù)器可以提供三類數(shù)據(jù):平均排隊長度;最大排隊長度;排隊車輛的停車次數(shù)。這里所指的排隊是從上游路段或連接器的排隊計數(shù)器的設(shè)置位置開始計數(shù),直至排隊狀態(tài)下的最后一輛車。從圖8可以看出,在現(xiàn)狀交通管理?xiàng)l件和道路條件下,高峰時段鼓樓隧道出口(南進(jìn)口)交叉口出現(xiàn)了嚴(yán)重的排隊現(xiàn)象,已經(jīng)排到隧道里面,故該段隧道出口銜接段長度設(shè)置有待完善。通過改善優(yōu)化后,重新建立仿真,得到仿真效果如圖9所示,在該銜接段長度上,排隊長度已經(jīng)減小。由輸出數(shù)據(jù)表3和表4中也可以看出兩種情況的排隊長度是有差別的,故證明該銜接段長度模型有可行性。
4.4 具體改善措施
為了盡量減少工程量,對現(xiàn)狀的銜接段長度不做大的改動,根據(jù)鼓樓隧道出口與其相鄰交叉口的實(shí)例仿真,利用建立的銜接段長度模型,可以提出相應(yīng)的交通管理改善方案。為減少隧道出口車輛的排隊長度,同時采取以下3種措施。
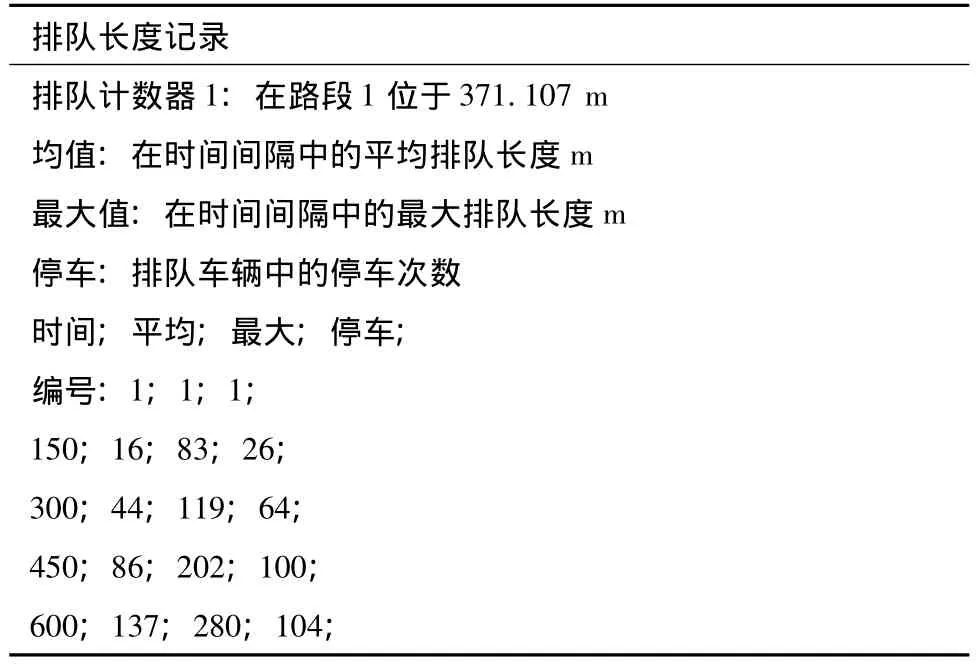
表4 改善后排隊長度檢測數(shù)據(jù)輸出表Tab.4 Output of the detected queues after improvement
(1)調(diào)整中央路—傅厚崗交叉口信號配時,盡量增加南北向直行的綠燈時長,提高中央路的通暢性,減少車輛排隊長度。
(2)拓寬傅厚崗東側(cè)一個出口車道,保證東西向不發(fā)生延誤。
(3)適當(dāng)降低隧道的設(shè)計車速,從而減少隧道出口車輛的排隊長度。
5 結(jié)束語
本文從城市隧道出口交通流特性出發(fā),根據(jù)駕駛?cè)艘曈X適應(yīng)能力、隧道出口道路線形及車速等因素的分析,確定隧道出口的安全距離;并通過對相鄰交叉口的排隊延誤分析,提出了適應(yīng)此類交通流特性的排隊優(yōu)化模型。該模型分別考慮了隧道出口和交叉口兩個方面的不同因素,在已建城市隧道出口實(shí)際銜接長度不滿足理論值的情況下,為減少對銜接路段的施工,可通過現(xiàn)狀交通流相關(guān)數(shù)據(jù)帶入長度模型,改變交叉口信號配時、限制隧道出口車速等相關(guān)交通管理措施,來緩解交通擁擠,提高行車效率與安全性,同時該長度模型對新建隧道出口銜接路段設(shè)計有重要參考價值。以上研究是根據(jù)玄武湖隧道出口的數(shù)據(jù)而進(jìn)行的分析,具有一定的特殊性,隨著研究和實(shí)踐的深入,模型將會得到進(jìn)一步的完善。
[1]DGJ08-96,城市道路平面交叉口規(guī)劃與設(shè)計規(guī)程[S].
[2]劉 韻.城市地下快速道路建設(shè)動因分析[J].地下空間與工程學(xué)報(增刊),2006,2(8):1293 -1296.
[3]李素艷,楊東援,趙婭麗.地下道路出入口交通組織研究[J].地下空間與工程學(xué)報,2007,3(4):781 -786.
[4]杜志剛,潘曉東,楊 軫,等.高速公路隧道進(jìn)出口視覺震蕩與行車安全研究[J].中國公路學(xué)報,2007,20(5):101 -105.
[5]郭忠印.公路隧道進(jìn)出口運(yùn)行安全研究——中期報告[R].上海:同濟(jì)大學(xué),2005.
[6]郭忠印,孔令旗.隧道進(jìn)出口運(yùn)行安全研究[R].上海:同濟(jì)大學(xué),2008.
[7]楊 軫,郭忠印.隧道進(jìn)出口車速變化研究[J].上海公路,2006,1:48 -51.
[8]DG/TJ08-2033-2008,道路隧道設(shè)計規(guī)范[S].
[9]雋志才,魏麗英,李 江.信號交叉口排隊長度宏觀模擬的自適應(yīng)分析法[J].中國公路學(xué)報,2000,13(1):77 -80.
[10]周學(xué)農(nóng).排隊長度模型比較及動態(tài)方法研究[J].交通運(yùn)輸系統(tǒng)工程與信息,2006,6(1):91 -95.
[11]顏桃為,馬健霄,馬 亮.信號交叉口安全評價體系研究[J].森林工程,2010,26(1):49 -52.
[12]榮 建,何 民,陳春妹.信號交叉口排隊長度動態(tài)計算方法研究[J].中國公路學(xué)報,2002,15(3):101 -104

