漸開線直齒圓柱齒輪設計中的接觸應力研究

杜 鈞，張 英，趙堂春

（北京電子科技職業學院自動化工程學院，北京 100176）

0 引 言

齒輪傳動機構中，輪齒是齒輪直接參與工作的部位，常見的失效現象多發生于輪齒上，設計中的接觸應力分析是強度校核的重要基礎。

1 設計應滿足的條件

1.1 一對漸開線齒輪正確嚙合的條件分析

一對漸開線齒廓雖能保證確定的傳動比，但不表明任意兩個漸開線齒輪都能搭配起來進行正確嚙合傳動。要實現運動和動力的傳動，必須滿足一定條件。圖1出示一對漸開線齒輪的嚙合瞬間，此時有兩對齒參與嚙合，兩輪齒工作側齒廓的嚙合點分別為K和K'。為了保證確定的傳動比，兩嚙合點K和K'必須同時落在嚙合線N1N2上；否則，將出現卡死或沖擊的現象。這一條件可表述為和分別為齒輪1和齒輪2相鄰同側齒廓沿公法線上的距離，稱為法向齒距，用pn1、pn2表示。因此，一對齒輪實現定比傳動的正確嚙合條件為兩輪的法向齒距相等。又由漸開線性質知，齒輪法向齒距與基圓齒距相等，則該條件又可表述為兩輪的基圓齒距相等，即pb1=pb2.若將 pb1=πm1cosα1和 pb2=πm2cosα2，代入則得 ： m1cosα1=m2cosα2.

式中：m1、m2和α1、α2分別為兩輪的模數和壓力角。由于齒輪模數和壓力角都已標準化，可取：m1=m2=n.α1＝α2=α.兩輪的法向齒距相等，因此，漸開線直齒圓柱齒輪的正確嚙合條件最終表述為：兩輪的模數和壓力角分別相等。

1.2 實現連續傳動的條件分析

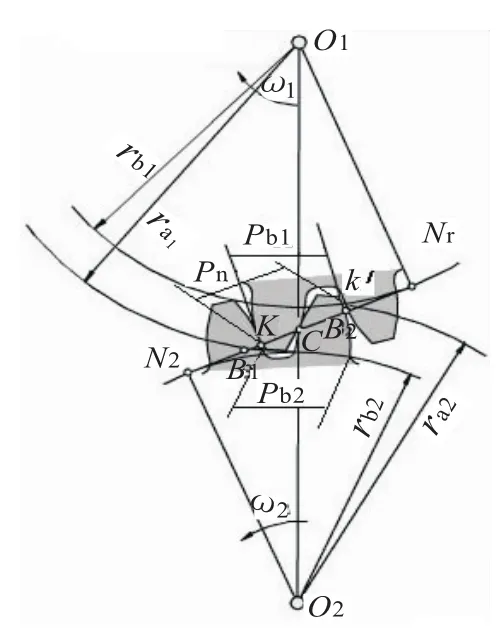
圖1 一對漸開線齒輪的嚙合

1）一對漸開線齒輪嚙合傳動的過程：齒輪傳動通過輪齒交替嚙合實現。見圖1，主動輪o1順時針方向轉動，推動從動輪o2逆時針方向轉動。一對輪齒的開始嚙合點是從動輪齒頂圓η2與嚙合線 N1N2的交點 B2，這時主動輪的齒根與從動輪的齒頂接觸，兩輪齒進入嚙合。隨著嚙合傳動進行，兩齒廓的嚙合點將沿著嚙合線向左下方移動，直到主動輪的齒頂圓η1與嚙合線的交點B1，主動輪的齒頂與從動輪的齒根即將脫離接觸，兩輪齒結束嚙合，B1點為終止嚙合點。線段B1B2為嚙合點的實際軌跡，稱為實際嚙合線段。若兩輪齒頂圓加大時，點B1、B2分別趨于點N1、N2，實際嚙合線段將加長。但因基圓內無漸開線，故點B1、B2不會超過點N1、N2，故點N1、N2稱為極限嚙合點。線段N1N2是理論上最長的實際嚙合線段，稱為理論嚙合線段[1]。

2）連續傳動應滿足的條件：為保證齒輪定傳動比的連續性，僅有兩輪基圓齒距相等的條件是不夠的，還須滿足B1B2≥Pb。否則，當前一對齒廓在點B1分離時，后一對齒廓尚末進入點B2嚙合，這使前后兩對輪齒交替時將會引起沖擊，無法保證傳動的平穩性。兩漸開線曲面的彈性體在齒廓傳動壓力下相互接觸，都會產生接觸應力，這種傳遞動力的高副機構工作中往往出現交變應力。受交變接觸應力的機器零件在一定的條件下會出現疲勞點蝕現象，點蝕擴散到一定程度，零件就不能再用了，失效了，稱為疲勞點蝕破壞。齒輪傳動中的疲勞點蝕是其常見的一種失效形式，又因這種交變應力，進而會產生齒廓的塑性變形和齒廓折斷等失效現象，要保證漸開線直齒圓柱齒輪正確嚙合和連續傳動，接觸應力的分析是設計的關鍵，所以，兩對齒輪的重合度對接觸應力存在著一定的影響[1]。

3）重合度：實際嚙合線段B1B2與基圓齒距pb的比值稱為重合度εα，見圖2。

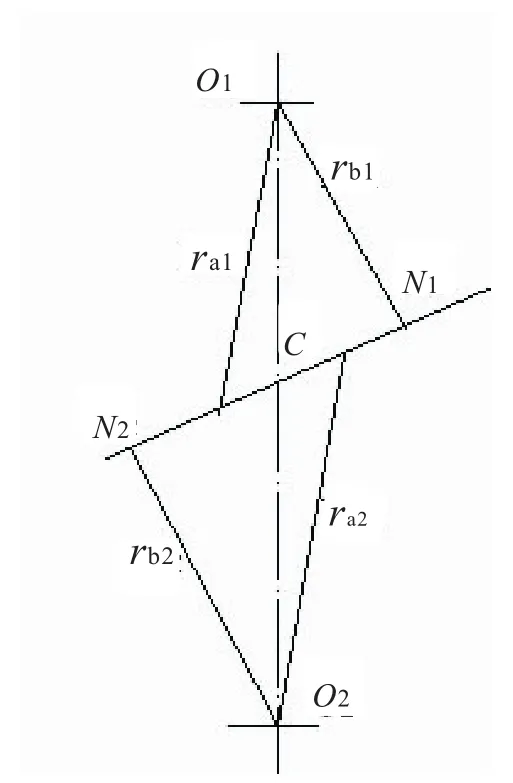
圖2 重合度

重合度表達為：εα=(B1B2)/pb≥1.實際應用中，εα值應大于或等于一定的許用值[εα]，即 εα≥[εα].其中許用重合度[εα]的值是隨齒輪的使用要求和制造精度而定，推薦的[εα]值可查找相應標準[2]，常用的見表1。

表1 [εa]推薦表

一對外嚙合齒輪的實際嚙合線段B1B2=B1P+B2P.由于B1P=B1N1-PN1=mz1cosα(tgαa1-tgα')/2.B2P=B2N2-PN2=mz2cosα(tgαa2-tgα')/2.可得：

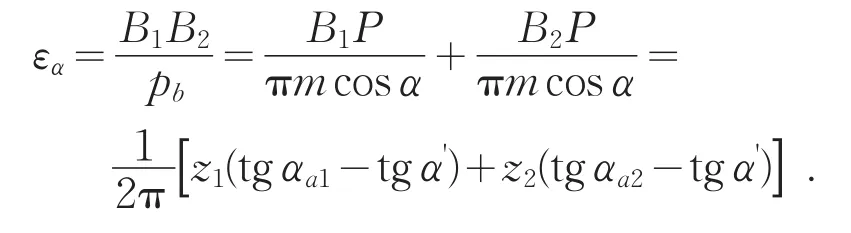
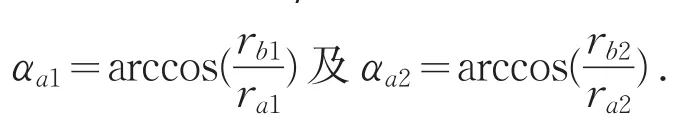
4）兩齒廓的嚙合傳動中，重合度的物理意義：重合度的大小表明同時參與嚙合的輪齒對數的多少。見圖3的εα=1.3情況，實際嚙合線B1B2的B2A1和A2B1（長度各為0.3Pb）段有兩對輪齒同時在嚙合，即為雙齒嚙合區；而在節點P附近A1A2段（長度為0.7Pb），只有一對輪齒在嚙合，即為單齒嚙合區[2]。總之，εα值愈大，表明同時參加嚙合輪齒的對數愈多，在相同載荷的條件下其應力分布較為分散，不僅對提高齒輪傳動的承載能力和傳動的平穩性都有重要意義，而且能夠減弱疲勞點蝕破壞，提高齒輪的使用壽命。

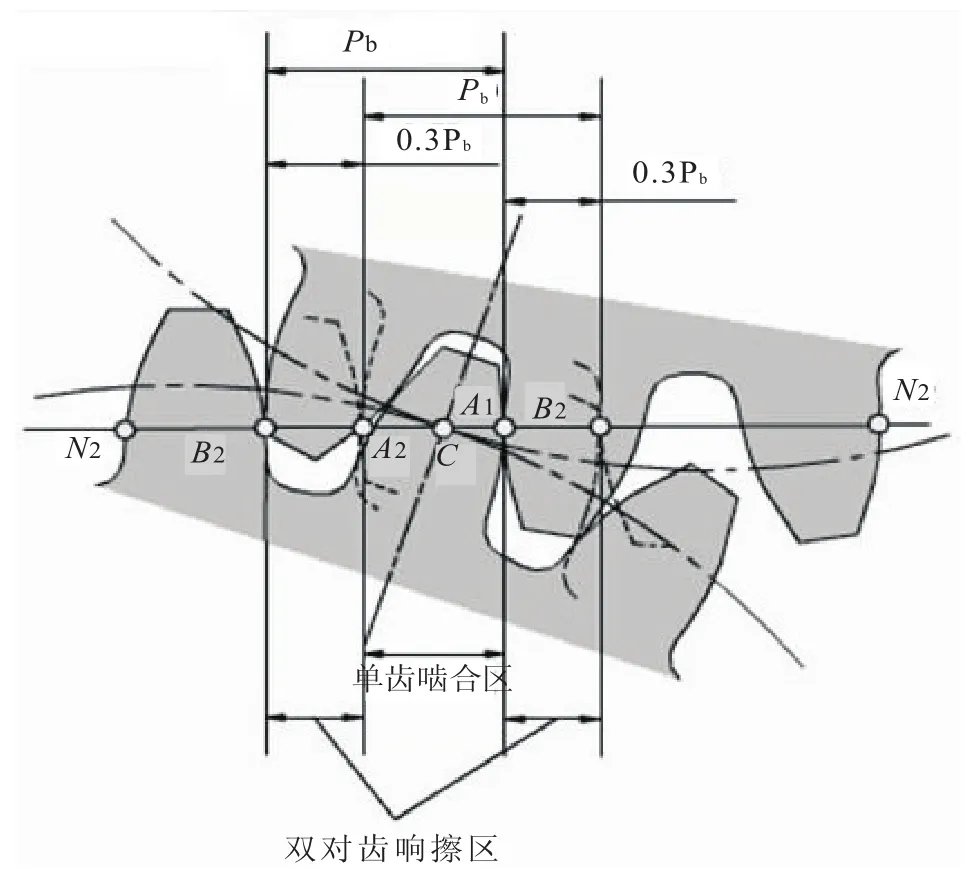
圖3 重合度的意義

2 軸線平行的兩圓柱體接觸時的接觸應力

軸線平行的兩圓柱體接觸時，變形前二者沿一條直線接觸，受壓力P后，接觸處發生了彈性變形，接觸線變成寬度2b的矩形面，見圖4，接觸面上的單位壓力按橢圓柱規律分布[3]。變形最大的x軸上壓力最大，以P0表示，接觸面上其余各點的壓力按半橢圓規律分布，見圖5，半橢圓柱的體積等于總壓力P，故

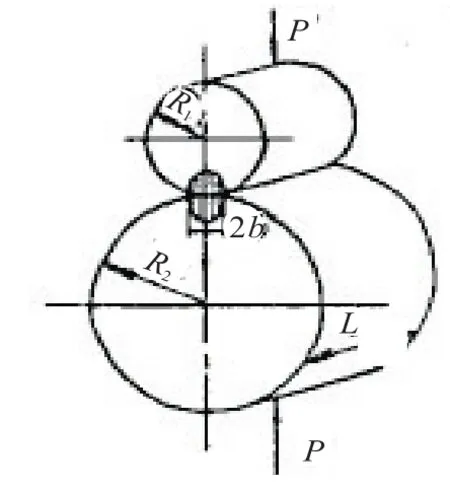
圖4 兩圓柱體接觸

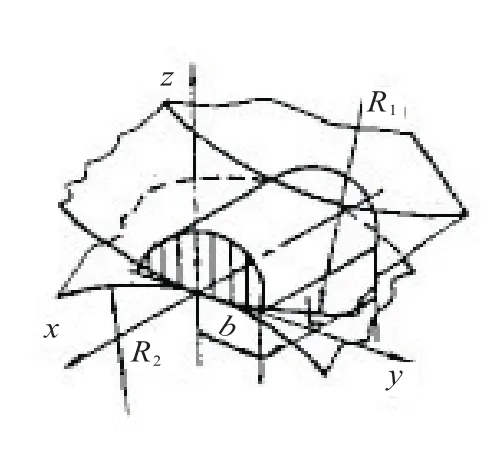
圖5 兩圓柱體接觸的壓力分布

最大單位壓力：

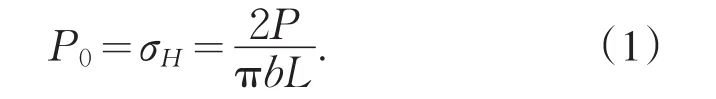
由赫茲公式知：

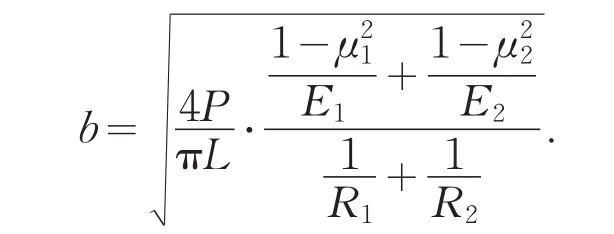
代入式（1）得

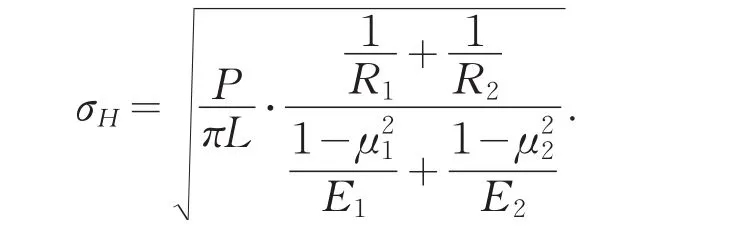
若兩圓柱體的材料均為鋼時，E1＝E2＝E，μ1＝μ2＝0.3，取

.則接觸應力為：

3 齒輪傳動齒廓的接觸應力分析

一對齒輪在節點處接觸，相當于半徑為ρ1、ρ2的兩個圓柱體接觸，見圖6，則其曲率半徑為：

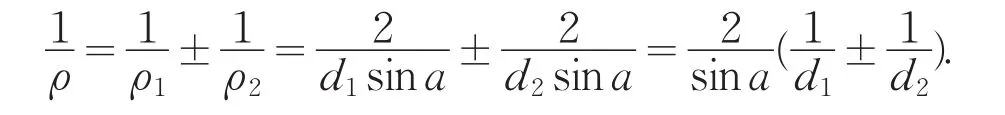
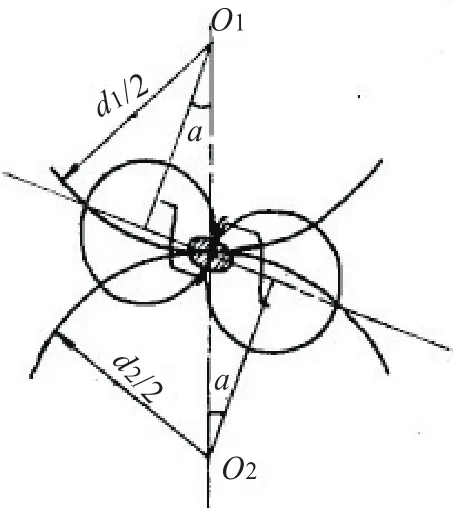
圖6 一對齒輪在節點處接觸的接觸應力

4 結束語

1）經對漸開線曲面間高副接觸應力的分析，并用赫茲公式可知，齒輪材料確定的條件下，齒輪的結構與接觸應力有著直接關系，在相同載荷的情況下，其分度圓的直徑越大，可承受的接觸應力就會有所提高；壓力角越大，可承受的接觸應力值會下降。2）對于齒輪傳動，通常是工作在較高的接觸壓力下，使其經過多次接觸應力循環后，局部表面將有小片或小塊金屬剝落、形成麻點或凹坑，使零件工作時噪音增大，振動加劇。如果在其結構設計時，根據上述接觸應力赫茲公式分析，進行相應結構考慮，對于提高齒輪使用壽命很有實際意義。

[1] 周亞焱，程友斌.機械設計基礎[M].北京:化學工業出版社,2008:107-108.

[2] 韓建友.機械原理[M].北京:高等教育出版社,2007：279-282.

[3] 劉鴻文.材料力學[M].北京:高等教育出版社,1984：268-270.