基于兩種改進方法的電能質量綜合評估

何吉彪，程浩忠，姚良忠，Masoud Bazargan

（1.上海交通大學電氣工程系電力傳輸與功率變換控制教育部重點實驗室，上海 200240；2.國網電力科學研究院，南京210061；3.阿爾斯通電網集團研究與技術中心，斯塔福德ST17 4LX，英國）

我國現有七項電能質量標準，分別對電壓偏差、頻率偏差、諧波、間諧波、電壓三相不平衡度、電壓波動與閃變、暫時過電壓和瞬態過電壓進行了限定，且目前電能質量測量儀能夠判斷這些電能質量指標是否滿足標準要求[1]。但如何從總體上對電能質量做出綜合評價現在仍然是研究的難點和熱點之一。

文獻[2]在國家標準規定的相關電能質量指標限值基礎上，建立了同一尺度下的統一型電能質量指標體系，提出了一種基于雷達圖法的電能質量綜合評估方法。文獻[3]通過主觀權重和客觀權重的組合來構建電能質量的綜合指標，但其客觀權重的確定方法還值得商榷。文獻[4]用二階段線性規劃的方法得到各項指標權值，然后采用概率統計的方法將各項指標綜合量化，得到綜合評價電能質量的唯一量化指標。文獻[5]構造出模糊神經識別網絡，構建了電能質量綜合評估的模糊神經網絡模型。目前的電能質量評估方法逐漸趨向于復雜化，在實際推廣應用中可能會造成一定的困難。

本文通過分析AHP中判斷矩陣的不一致性與比較矩陣的關系，調整對一致性影響最大的元素，得到合理的權值。分別以電能質量國標中的規定值和限制值作為加權TOPSIS的絕對理想解和絕對負理想解，改進了加權TOPSIS法只對各個評價對象排序而無法進行定性分級的不足，同時解決了逆序的問題。該綜合評估方法操作簡便易行，可以根據不同類型的負荷的敏感程度來確定各單項指標的不同權重，所得評估結果客觀，合理。

1 層次分析法和加權TOPSIS法的改進

1.1 層次分析法的改進

層次分析法是一種定性與定量相結合的決策分析方法。它的基本思路可以分為以下4個步驟。

（1）將復雜的問題層次化，形成由目標層、準則層、指標層和方案層組成的遞階層次結構；

（2）采用“1-9標度法”，規則如表1所示，形成判斷矩陣；

（3）檢驗判斷矩陣的一致性；

（4）通過逐層計算，得到方案層對目標層的權重，確定出最優方案。

表1 判斷矩陣標度及含義Tab.1 Scale and meaning of judgment matrix

AHP法的關鍵是要給出一個具有一致性的判斷矩陣A=（aij）n×n。通過設定一個比較矩陣P，可對影響最大的元素進行微調，改進判斷矩陣的一致性。

改進判斷矩陣一致性的方法步驟如下。

步驟1 由評估專家給出判斷矩陣An×n的上三角元素，根據aij=1/aji的準則確定下三角元素，保證A為正互反矩陣；

步驟2 計算判斷矩陣A的排序權值ω；

步驟3求出比較矩陣P=（pij）n×n，

令

稱矩陣P=（pij）n×n為判斷矩陣A的比較矩陣；

步驟4 將矩陣P中絕對值最大的元素pij的下標 i，j對應記為 s，t；

步驟5 當pst>0時，若ast為整數，令ast′=ast-1，若ast為分數，令ast′=1/（1/ast+1）；

當 pst<0 時，若 ast為整數，令 ast′=ast+1，若 ast為分數，令ast′=1/（1/ast-1）；

步驟6 令 ats′=1/ast′，aij′=aij，i，j=1，2，…，n且 i，j≠s，t；

（7）計算新生成矩陣 A′=（aij′）n×n的 CR 值，若CR（A′）<0.1，A′即為所求；否則，將矩陣 A′代入步驟1繼續求解。

進行上述求解步驟的原因是矩陣A為完全一致性矩陣的充要條件是矩陣P中元素全部為0，即pij=0。因為，若判斷矩陣A為完全一致性矩陣，則有 aij= ωi/ωj，從而 pij=0（i，j=1，2，…，n）；若有 pij=0（i，j=1，2，…，n），從而 aij= ωi/ωj，即 A 為完全一致性矩陣。

由此可知，判斷矩陣A是否為完全一致性矩陣可由P中是否存在不為0的元素判斷。aij對A的不一致性的影響越大則對應的pij偏離0越大。一般情況下，專家給出的判斷矩陣不會出現較大偏差，可通過對影響最大的元素增減1來逐步改進判斷矩陣的一致性。當pij>0時，aij偏大，應該減小；當pij<0時，aij偏小，應該增大。

1.2 加權TOPSIS法的改進

1.2.1 加權TOPSIS法及逆序問題

在多指標的決策問題中，TOPSIS法是一種逼近理想解的排序方法，借助于多指標問題中的正理想解和負理想解對方案集中的各方案進行排序。在歐氏空間中，離正理想解距離越近、而離負理想解距離越遠的方案越優。正理想解是方案集中并不存在的虛擬的最佳方案，其每個指標值都是決策矩陣中該指標的最優值；負理想解則是虛擬的最差方案，其每個指標值都是該指標的最差值。而加權TOPSIS法強調了參與評估的各指標重要性的不同，使評價結果更趨合理。

逆序是指當使用加權TOPSIS法時，n個方案x1，x2，…，xn的評價結果是方案xi優于xj（i≠j），但是當增加（或減少）若干個方案后，得出的結果卻是方案xj優于xi，這就是逆序問題[7]。逆序問題將使得原來所做的所有工作（包括最后的決策結果）都變得毫無意義。

假設有兩個指標均為高優指標，每一個屬性的權值相等，即w1=w2=0.5；設有5個可行方案，分別為

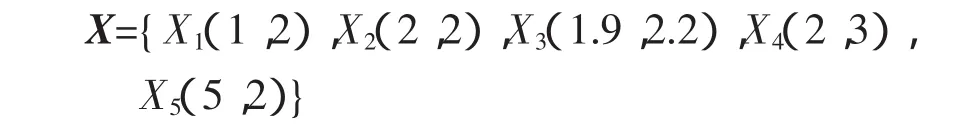
按照傳統的TOPSIS法進行計算，當考慮前4個方案時，規范化預處理各方案的原始數據，有

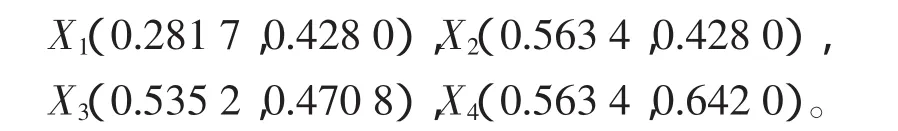
最后的排序結果為

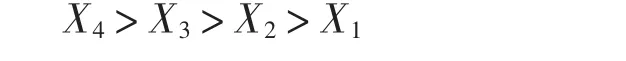
當考慮5個方案時，對方案的原始數據進行規范化預處理，有

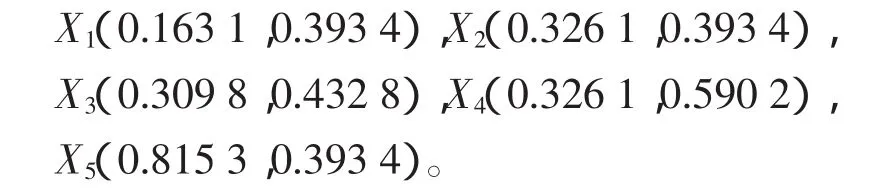
最后的排序結果為

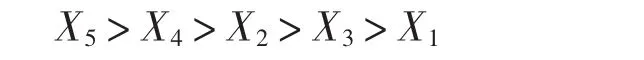
由上面兩次的結果可知，X2和X3在方案增加前后的排序不同，即出現了逆序。對于給定的兩組方案的數據，雖然指標值的變化都是保序變化，但是在兩次決策中的理想解是不同的。在只有前4個方案的方案集中，多指標問題的正理想解為（0.563 4，0.642 0），負理想解為（0.281 7，0.428 0）；當方案集中有5個方案時，多指標問題的正理想解為（0.815 3，0.590 2），負理想解為（0.163 1，0.393 4）。可見方案的增加（或減少）造成的影響是引起了正理想解、負理想解和參照標準的改變，從而可能導致逆序的產生。

如果簡單地將加權TOPSIS法應用于電能質量的綜合評估，除了存在逆序問題之外，還有一個問題是，它只能對各個評估對象進行排序，選出電能質量較好的一個，但是不能評估其好壞程度，無法與電能質量的國標值聯系，以國標值為參考進行評估。

1.2.2 加權TOPSIS法的改進

由上述分析可知，正理想解和負理想解的改變是TOPSIS法產生逆序的一個很重要的原因。為了克服這一缺點，引入絕對正理想解和絕對負理想解，同時結合電能質量評估的特點，將電能質量國標中的規定值作為絕對正理想解，限制值作為絕對負理想解，添加到評價對象的數據矩陣中一起進行運算處理，不僅可以對各評估對象進行排序，克服逆序問題，還能以國標為準則判斷對象是否合格并進行定性分級。

改進后的加權TOPSIS法的步驟如下。

（1）以電能質量國標中的規定值為理想解，限制值為負理想解；

（2）將理想解和負理想解指標與各評估對象的數據一起進行同趨勢化和歸一化處理；

（3）計算理想解與負理想解之間的距離D；

（4）計算各評估對象與理想解和負理想解間的距離Di+和Di-；

（5）計算各評估對象與理想解的接近程度Ci；

（6）根據D與Di+的關系判斷評價對象是否合格，由Ci對合格的評估對象進行分級評估。

2 基于改進AHP和加權TOPSIS法的電能質量綜合評估

上文對層次分析法和加權TOPSIS法的改進進行了闡述，基于兩者的電能質量綜合評估的具體方法如下。

假設針對m個評估對象的電能質量情況進行綜合評估，評價的電能質量指標類型為n個，則數據矩陣為 Xm×n。

（1）運用改進的AHP法求解各電能質量指標的權值，得到權值相量 ω =（ω1，ω2，…，ωn）T。

（2）將n個電能質量指標對應的國標中的規定值和限制值分別設定為理想解和負理想解。

（3）數據的同趨勢化和歸一化。

將理想解與負理想解加入到評估對象的指標數據矩陣中，得矩陣為 X（m+2）×n。

一般的電能質量指標為低優指標，如頻率偏差、閃變、諧波畸變率等，都是數值越小越好。如果有不同趨勢的指標，可用倒數法或插值法將所有指標同趨勢化，所得矩陣為 X′（m+2）×n。

同趨勢化后，為了消除計量單位的影響，需要按照式（2）進行向量歸一化處理，得到歸一化矩陣Z中元素為

分別用 Z+=（Z1+，Z2+，…，Zn+）和 Z-=（Z1-，…，Zn-）表示評價指標的理想解與負理想解。+為處理后的第j個電能質量指標的國標規定值為處理后的第j個電能質量指標的國標限制值。

（4）計算理想解與負理想解之間的距離D。

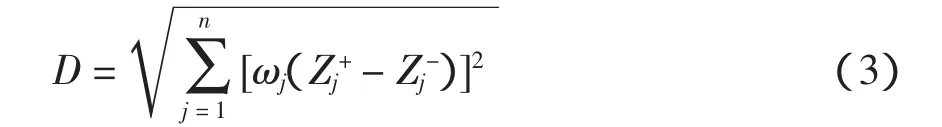
（5）計算各評估對象的指標值與理想解及負理想解之間的距離和，計算公式為

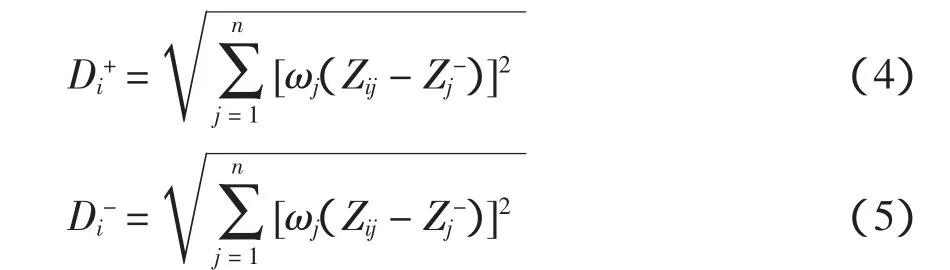
（7）計算合格的評估對象與理想解的接近程度為

圖1 電能質量綜合指標分級Fig.1 Grading of power quality comprehensive indexes

3 實例應用分析

用本文提出的電能質量綜合評估方法對兩個光伏發電系統的電能質量情況進行評估。這兩個光伏發電系統分別安裝于兩個110 kV變電站的站用電系統中，系統A容量為4.8 kW，系統B容量為30 kW。評估的基礎為在光伏發電系統并網點測得的實際數據。

案例中選取的電能質量指標為兩個系統的電能質量測量結果中共有的指標，包括電壓偏差、閃變、諧波畸變率、三相不平衡度、頻率偏差；經過專家調查，按表1規則給出判斷矩陣A。如果采用更多的單項評估指標，可采用相同的方法進行評估，只是判斷矩陣的維數不同。

用第1.1節的方法求得的權重相量為

ω =（0.1844 0.1063 0.4589 0.1844 0.0660）T

將兩個光伏發電系統測得的各項電能質量指標數據與國標規定值和限制值一起同趨勢化和歸一化后，所得的矩陣為

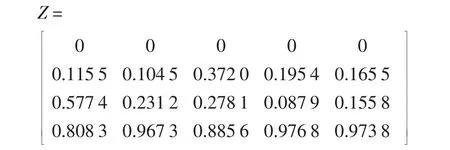
其中第一行為理想解，最后一行為負理想解。

用式（3）～式（5）計算得到兩個光伏發電系統的電能質量評估結果如表2所示。

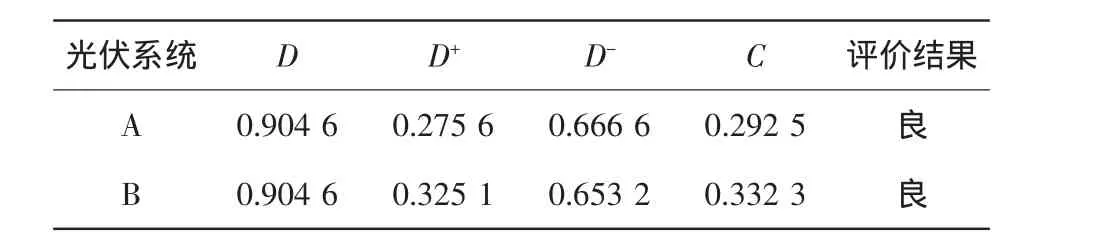
表2 評估結果Tab.2 Results of evaluation

首先兩個系統的D+值均小于D值，表明兩個系統的指標值均合格。再根據圖1的分級標準，兩個光伏發電系統的電能質量綜合評估結果均為良。系統A的C值小于系統B的C值，說明系統A的電能質量綜合評估結果比系統B更接近于國標的規定值，更遠離國標的限制值，所以光伏發電系統A的電能質量綜合情況優于系統B。系統A的容量小于系統B，評估結果說明了光伏發電系統容量增大將對所接入的電網的電能質量造成更大的影響，體現了該方法的合理性。

4 結論

（1）通過分析判斷矩陣的不一致性與比較矩陣的關系，簡單有效地改進了判斷矩陣的一致性，得到更為合理的指標權重。

（2）將電能質量國標的規定值設為理想解，限制值設為負理想解，解決了將加權TOPSIS法應用于電能質量評估時可能產生的逆序問題，以及彌補了只對各個評價對象排序而無法進行定性分級的不足，結合改進AHP所得的權值，使得評估方法更加簡便，具有實用性。

（3）通過案例的實際應用，得到了綜合性的分級評估結果，證明了這種方法的簡便易行，可以客觀、全面、合理地對評估對象的電能質量進行綜合評估，具有較好的應用價值。

[1]譚家茂，黃少先（Tan Jiamao，Huang Shaoxian）.基于模糊理論的電能質量綜合評價方法研究（Research on synthetic evaluation method of power quality based on fuzzy theory）[J].繼電器（Relay），2006，34（3）：55-59.

[2]李國棟，李庚銀，楊曉東，等（Li Guodong，Li Gengyin，Yang Xiaodong，et al）.基于雷達圖法的電能質量綜合評估模型（A comprehensive power quality evaluation model based on radar chart method）[J].電力系統自動化（Automation of Electric Power Systems），2010，34 （14）：70-74.

[3]劉兵，李群湛，董祥（Liu Bing，Li Qunzhan，Dong Xiang）.基于時變權重的電能質量綜合評估研究（Comprehensive assessment study of the power quality based on the timevarying weight）[J].電力系統保護與控制（Power System Protection and Control），2009，37（14）：6-9.

[4]熊以旺，程浩忠，王海群，等（Xiong Yiwang，Cheng Haozhong，Wang Haiqun，et al）. 基于改進 AHP 和概率統計的電能質量綜合評估（Synthetic evaluation of power quality based on improved AHP and probability statistics）[J].電力系統保護與控制（Power System Protection and Control），2009，37（13）：48-52，71.

[5]周林，栗秋華，劉華勇，等（Zhou Lin，Li Qiuhua，Liu Huayong，et al）.用模糊神經網絡模型評估電能質量（E－valuation of power quality by fuzzy artificial neural network）[J]. 高電壓技術 （High Voltage Engineering），2007，33（9）：66-69.

[6]陶順，肖湘寧（Tao Shun，Xiao Xiangning）.電力系統電能質量評估體系架構（Infrastructure of the power quality assessment system of power systems）[J].電工技術學報（Transactions of China Electrotechnical Society），2010，25（4）：171-175.

[7]黃德才，鄭河榮（Huang Decai，Zheng Herong）.理想點決策方法的逆序問題與逆序的消除（Study on the problem and elimination of rank reversal existing in ideal point multiple attribute decision making）[J].系統工程與電子技術（Systems Engineering and Electronics），2001，23（12）：80-83.

[8]張弛，程浩忠，奚珣，等（Zhang Chi，Cheng Haozhong，Xi Xun，et al）.基于層次分析和模糊綜合評價法的配電網供電模式選型（A study of distribution network feeding modes selection based on analytic hierarchy process and fuzzy comprehensive evaluation）[J].電網技術（Power System Technology），2006，30（22）：67-71.

[9]周群艷，田澎，田志友（Zhou Qunyan，Tian Peng，Tian Zhiyou）.基于幾何一致性指數的判斷矩陣一致性改進（Consistency improvement of comparison matrix based on geometric consistency index）[J].西南交通大學學報（Journal of Southwest Jiaotong University），2006，41（2）：236-240.

[10]Tanaka H，Tsukao S，Yamashita D，et al.Multiple criteria assessment of substation conditions by pair-wise comparison of analytic hierarchy process[J].IEEE Trans on Power Delivery，2010，25（4）：3017-3023.

[11]張曉花，陳星鶯，劉皓明，等（Zhang Xiaohua，Chen Xingying，Liu Haoming，et al）.一種新策略在電能質量綜合評價中的應用（Application of a novel strategy in the comprehensive evaluation of power quality）[J].電力系統及其自動化學報（Proceedings of the CSU-EPSA），2008，20（6）：41-46.

[12]胡文錦，武志剛，張堯，等（Hu Wenjin，Wu Zhigang，Zhang Yao，et al）.風電場電能質量分析與評估（Analysis and evaluation on the electric power quality of the wind farm）[J].電力系統及其自動化學報（Proceedings of the CSU-EPSA），2009，21（4）：82-87.