復合材料層合板的振動模態試驗研究

漆文凱，程 博，劉 磊

（南京航空航天大學能源與動力學院，南京210016）

復合材料層合板的振動模態試驗研究

漆文凱，程 博，劉 磊

（南京航空航天大學能源與動力學院，南京210016）

采用逐點激勵單點測試（SISO）的方法，在自由狀態和一端固支狀態下對無損傷和含開孔損傷的復合材料層合板進行了模態試驗和模態識別。根據測量得到的試驗件的頻率、阻尼和振型等模態參數，分析了層合板在不同邊界條件下開孔損傷位置和開孔損傷大小對層合板的振動特性的影響。結果表明：復合材料層合板具有優越的阻尼特性；試驗獲得的振動特性與相關文獻中的結果一致；開孔損傷位置和開孔損傷大小對層合板的振動特性有明顯影響。

復合材料層合板；模態試驗；固有頻率；阻尼

0 引言

層合結構復合材料構件廣泛應用于現代結構設計中，其振動特性由于諸如非線性因素、材料的不均勻性和阻尼機理的復雜性等，單純采用有限元法，其計算的準確性（甚至于可能性）受到限制。在20世紀60～70年代發展起來的現代模態試驗分析技術彌補了有限元分析技術的某些不足。A.S.Hadi and J.N. A shton[1]從理論、試驗2方面對纖維方向、纖維體積分數與單向玻璃纖維/環氧樹脂復合材料阻尼特性的關系進行了研究；李頂河等[2]對一端固支含圓形孔損傷平面編織層合板的固有動力特性進行了試驗，研究了損傷尺寸對一端固支纖維雙向層合板固有頻率的影響規律；Vaidya[3]對3維空心結構機織E玻璃纖維復合材料進行了振動測試，利用半功率法得出所需阻尼比的值；李典森等[4]采用懸臂梁自由振動衰減試驗方法研究3維編制復合材料的振動阻尼特性，分析編織角、纖維體積分數和編織結構對3維編織復合材料振動阻尼特性的影響；楊和振[5]對復合材料層合板一端固支條件下的動力響應進行測試，采用隨機子空間法識別模態參數，分析了環境條件變化對復合材料層合板振動特性(固有頻率、阻尼以及振型)的影響；Berthelot[6]對玻璃纖維和芳綸纖維復合材料一端固支條件下的動力響應進行測試，通過激光測振儀拾振，獲得所需頻響函數、固有頻率和模態振型等；Hao[7]對復合材料黏彈性夾層梁簡支條件下的剛度和模態進行了分析，將采集信號輸送到LMS-Cada-X數據軟件分析，然后對頻響函數曲線進行擬合得到模態參數值；姚學峰等[8]利用試驗模態分析方法對碳纖維/環氧樹脂編織結構增強復合材料的動態特性進行了試驗研究，確定了編織復合材料梁、管的振動模態參數與傳遞函數；肖漢林、周心桃[9]對復合材料圓柱殼在自由懸掛的邊界條件下進行了振動模態試驗研究，討論了不同鋪層角度、脫層方式、脫層大小對復合材料結構的固有頻率、振型的影響。駱志高等[10]對自制的、1 種45#鋼和尼龍66為主要成分的金屬塑料復合材料進行了模態試驗，測試其在受迫振動條件下的響應頻率與阻尼比。

本文采用逐點激勵單點測試（SISO）方法，對無損傷、開孔損傷情況下的復合材料層合板試驗件進行動力響應試驗，通過測試層合板試驗件的頻響函數曲線，對其進行模態識別，獲得相應的固有頻率和模態阻尼。通過試驗分析開孔位置、開孔大小等對層合板振動特性的影響規律，為復合材料層合板結構動力響應的理論分析和建模提供試驗依據。

1 試驗理論基礎

多年來，眾多學者提出的各種模態參數識別方法，大體上可分為時域法和頻域法2類。時域法是1種從時域響應數據中直接識別模態參數的方法，頻域法則是在測量頻響函數基礎上，利用最小二乘估計萃取模態參數的方法，也有人稱之為機械導納法或傳遞函數法。目前，工程中模態識別多采用頻域模態識別法這一公認的比較成熟和有效的方法，與時域模態識別法相比，頻域模態識別法的物理意義更加的明確，與此對應的信號采集和模態分析軟件模塊也很成熟，選擇較多。

黏性阻尼系統的振動微分方程為

對其進行傅里葉變換得到系統在頻率域中的運動微分方程

式中：（K-ω2M+jωC）為阻抗矩陣，其倒數即為傳遞函數矩陣。

由振動理論可知，對線性時不變系統，系統的任一點響應均可表示為各階模態的響應的線性組合。設系統的自由度為N，因此可對l點的響應寫成線性組合形式

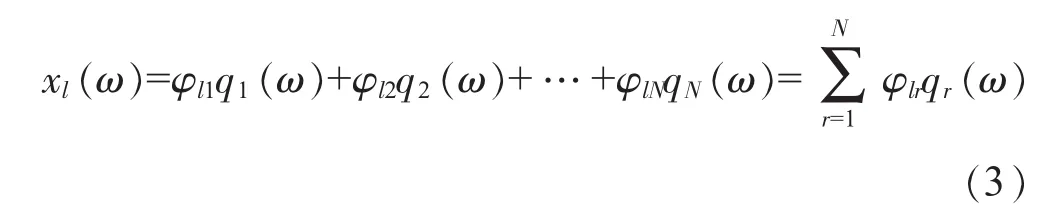
式中：φlr為第l個測點第r階模態的振型系數。

由式（2）可得第r階模態坐標為

對于單點激勵情況，設激勵作用于p點，則激勵力向量變為

則第r階模態坐標為

物理坐標中，系統任意一點l的響應為

因此測量點l與激勵點p之間的頻響函數為

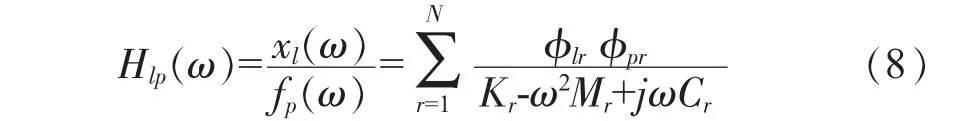
稍作變換后可得傳遞函數

式中：φlr、φpr分別為l、p 2點在第r階模態下的振型；Mr為模態質量；ωr為第r階自然頻率；ζr為第r階模態對應阻尼比。

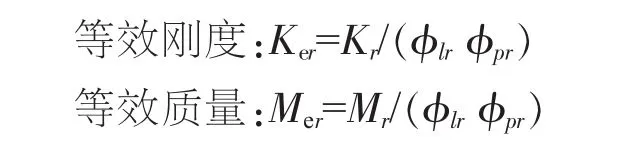
2 試驗描述

2.1 試驗方法與測試系統

2.1.1 自由狀態

在對結構系統進行模態試驗時，特別是結構部件，對于其實際的邊界條件，一般很難準確模擬，因而試驗時基本都設為“自由狀態”。因為在一般情況下，可以用軟橡膠繩懸掛來實現“自由狀態”，較其他狀態易于實現。而且，當結構處在自由狀態時，自由度是最多的，可以求得此無邊界約束狀態時的模態。只有未經約束的結構部件，才能與其他結構部件相連接實現所期望的約束，進行綜合模態分析。除自由狀態外，任何支承邊界都是有約束的邊界，或已經伴有自由度的縮減，從自由狀態過渡到自由度縮減或約束模態就容易得多。本文采用逐點激勵單點測試（SISO）的方法來進行層合板自由狀態下的模態試驗。層合板測試系統和測試網格劃分如圖1、2所示。

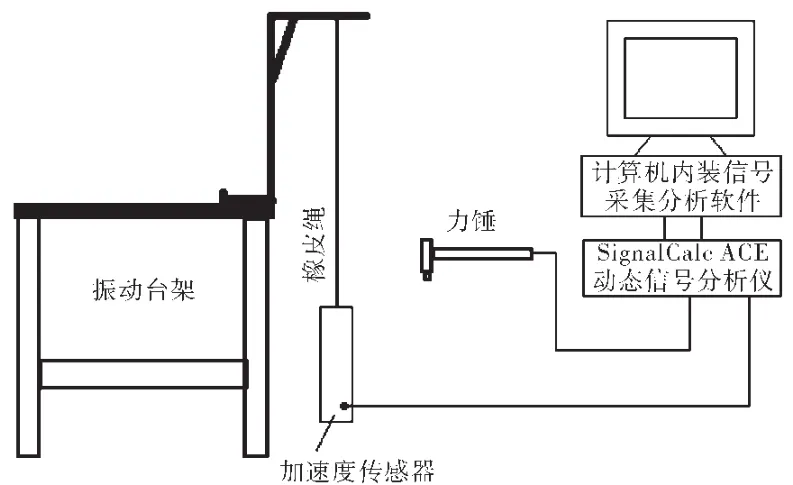
圖1 自由狀態層合板模態試驗測試系統

圖2 層合板測點網格劃分

2.1.2 一端固支狀態

通過夾緊塊裝置將層合板一端固定在振動臺架上，采用逐點激勵單點測量的方法對層合板進行模態試驗，對層合板劃分柵格來進行激勵點的變換，通過力錘和加速度傳感器獲得層合板一端固支狀態頻響函數，從而通過動態信號分析儀識別相應的模態參數。一端固支層合板模態試驗測試系統如圖3所示。

圖3 一端固支層合板模態試驗測試系統

采用美國SignalCalc ACE實時動態信號分析儀對層合板進行模態試驗和模態識別。用蜂蠟將加速度傳感器黏連于1號點位背面對應位置，連接好各測試設備；按標定值設置加速度傳感器和力錘的靈敏度，設定采樣頻率為2 kHz,平均采樣次數為3，選擇力窗，逐點激勵，采集繪制幅頻特性曲線（UFF）；試驗時，先用力錘對1號點分別進行3次脈沖激勵，采樣完成后保存數據，并繼續對2～18號點進行上述測試。

2.2 測試試件參數

試件為層合板T300/BMP316，鋪層方式均為[0]16,單層厚度為0.125 mm，自由狀態時有效長度為200 mm，一端固支時有效長度為180 mm，寬度為48 mm，

材料性能：E1=128.8 GPa；E2=E3=8.3 GPa；G12=G13=

4.1 GPa；G23=4.1 GPa，v=0.355，ρ=1578 kg/m3。

2.3 試驗數據采集及處理

圖4 層合板試驗簡化模型

采用ICATS模態分析軟件識別層合板的模態頻率、模態振型、模態阻尼。首先得將層合板測試點幾何模型導入ICATS建立試驗簡化模型，如圖4所示。

圖5 FRF模態參數識別

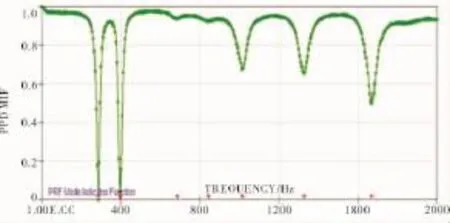
圖6 MIF頻響函數曲線模態識別

讀取UFF文件轉化為ICATS所需FRF文件，將FRF頻響函數曲線集成為1個.CRD文件，圈定頻響函數曲線峰值點來識別模態，擬合圓判斷所識別峰值的可靠性，如圖5所示；手動識別完模態參數后與MIF函數識別進行對比，如圖6所示，完成最終可靠模態的確定（其中遲滯阻尼η=2ξ）。讀取幾何參數文件和模態參數文件，動畫顯示各階模態振型、模態頻率和模態阻尼，通過動畫對層合板各階模態進行分析。

3 試驗結果及分析

3.1 自由支承試驗數據分析

通過軟橡膠繩懸掛層合板試驗件的方式來模擬層合板的自由狀態，對各試驗件進行模態試驗，測出了相應的模態參數。

表1 層合板不同開孔位置時模態振型（自由支承）

3.1.1 層合板不同開孔位置試驗數據分析

層合板不同開孔位置時，模態振型見表1。固有頻率和模態阻尼見表2。

從表1、2中可見，在自由狀態下對于單向層合板得出以下結論：

表2 層合板不同開孔位置時固有頻率和模態阻尼ξ（自由支承）

（1）此層合板的扭轉剛度比較小，扭轉振動模態比彎曲振動模態提前。

（2）開孔位置變化時，層合板的振型基本保持一致。

（3）對于低階振動，開孔損傷將使層合板的固有頻率普遍降低；對于高階振動，開孔損傷將使層合板的固有頻率普遍提高。

（4）層合板中間開孔損傷時的固有頻率變化量普遍高于兩端開孔時的固有頻率，說明自由狀態時，層合板的開孔位置越靠近中部對振動模態的影響越大。

（5）近懸掛端開孔試件和遠懸掛端開孔試件是開孔位置完全對稱的同一批規格材料，理論上自由支承時這2種試件的固有頻率應幾近相同，說明同一批材料不同試件之間振動特性差異的存在，應作為振動特性試驗分析的考慮因素。

3.1.2 層合板開孔大小不同試驗數據分析

層合板開孔大小不同時固有頻率和模態阻尼見表3。

從表3中可見，在自由狀態下對于單向層合板，固有頻率與開孔位置有關系。在中間開孔時，孔徑大小變化對固有頻率的影響都比較明顯；對于低階振動，開孔損傷將使層合板的固有頻率普遍降低；對于高階振動，開孔損傷將使層合板的固有頻率普遍提高；在開孔尺寸不是很大時，含開孔損傷層合板固有頻率隨孔徑變化不明顯，固有頻率隨著孔徑的增大而普遍降低。

3.2 一端固支試驗數據分析

表3 層合板開孔大小不同時固有頻率和模態阻尼ξ（自由支承）

表4 層合板不同開孔位置固有頻率和模態阻尼ξ（一端固支）

3.2.1 層合板不同開孔位置試驗數據分析

層合板不同開孔位置時固有頻率和模態阻尼見表4。

從表4中可見，在一端固支條件下，對于單向層合板不同開孔位置時損傷得出以下結論：

（1）固支狀態對層合板的扭轉剛度影響比較大，扭轉振動模態比彎曲振動模態滯后。

（2）固支狀態下開孔損傷基本都使得層合板固有頻率降低，對低階振動頻率影響不大，但對高階振動頻率影響卻較大。

（3）在一端固支情況下，靠近固支端開孔基本比自由端開孔固有頻率降低的多，說明固支端開孔對剛度的影響比自由端大。文獻[11]的數值模擬結果也表明，當穿孔損傷靠近固支端時，穿孔損傷對層合板剛度的影響要比對質量的影響強，穿孔使層合板固有頻率降低；當穿孔損傷遠離固支端時，穿孔損傷對層合板質量的影響要比對剛度的影響強，穿孔使層合板固有頻率增加。

表5 層合板開孔大小不同時模態振型（一端固支）

3.2.2 層合板開孔大小不同試驗數據分析

層合板開孔大小不同時，模態振型見表5，固有頻率和模態阻尼見表6。

從表5、6可見，在一端固支條件下對于單向層合板開孔大小不同變化時，層合板的振型基本保持一致；隨著開孔尺寸的增大，層合板的固有頻率基本是逐漸下降；孔徑很小時，層合板各階頻率變化不是很大。

表6 層合板開孔大小不同時固有頻率和模態阻尼ξ（一端固支）

4 結論

（1）在不同邊界條件下，開孔損傷對層合板固有頻率的影響不同。對于自由狀態，開孔損傷使層合板的低階固有頻率降低，高階固有頻率提高；對于懸臂狀態，開孔損傷使層合板固有頻率降低，低階固有頻率影響較小，高階固有頻率影響較大。

（2）當開孔位置變化時，層合板的振型基本保持一致。對于自由狀態，中間開孔損傷時的固有頻率變化量普遍高于兩端開孔時的固有頻率，說明自由狀態時，層合板的開孔位置越靠近中部對振動模態的影響越大；對于懸臂狀態，當穿孔損傷靠近固支端時，穿孔損傷對層合板剛度的影響要比對質量的影響強，穿孔使層合板固有頻率下降；當穿孔損傷遠離固支端時，穿孔損傷對層合板質量的影響要比對剛度的影響強，穿孔使層合板固有頻率增加。

（3）隨著開孔尺寸的增大，層合板的固有頻率基本呈逐漸降低的趨勢。

[1]Hadi S A，Shton J N.Measurement and theoretical modeling of the damping properties of a unidirectional glass-epoxy composites[J].Composite Structure,1996, 34（4）:381-385.

[2]李頂河，王軒，馮振宇，等.含孔損傷平面編織層合板固有頻率研究[J].玻璃鋼/復合材料，2009（1）:15-19. LI Dinghe,WANG Xuan,FENG Zhenyu，et al.Studay on natural frequency of plain woven fabric laminate with cutout [J].Fiber Reinforced Plastics/Composites,2009 （1）:15-19.(in Chinese)

[3]Vaidya A S,Uddin N.Vibration response of 3-D space accessible sandwich composite [J].Journal of Reinforced Plasticsand Composites,2009,28（13）: 1587-1599.

[4]李典森，盧子興，李嘉祿，等.三維編織復合材料振動阻尼特性的實驗研究[J].機械強度，2009,31（2）:211-214. LI Diansen,LU Zixing,LI Jialu，et al.Experimental research on the vibration damping propertiesof 3D braided composites[J].Journal of Mechanical Strength, 2009,31（2）:211-214.(in Chinese)

[5]楊和振，Park Hanil，李華軍．溫度變化下復合材料層合板的試驗模態分析 [J].復合材料學報，2008，125（12）：149-155．YANG Hezhen,Park Hanil,LI Huajun.Experimental modal analysis of the composite laminates with temperature variation [J].Acta Materiae Compositae Sinica，2008，125（12）：149-155．(in Chinese)

[6]Berthelot J M,Assarar M,Sefrani Y,et al.Damping analysis of composite materials and structures[J].Composite Structures,2008（85）3:189-204.

[7]HAO Min，RAO Mohan D．Vibration and damping analysis of a sandwich beam containing a viscoelastic constraining layer[J].Journal of Composite Materials,2005, 39（18）：1621-1643．

[8]姚學峰，姚振漢，戴福隆，等.編織結構復合材料動態特性的實驗模態分析[J].復合材料學報，1998,15（4）:107-112. YAO Xuefeng,YAO Zhenhan,DAI Fulong，et al.Experimetal modal ayalysis on dynamic characteristics of braided structral composites[J].Acta Materiae Compositae Sinica,1998,15（4）:107-112.(in Chinese)

[9]肖漢林，周心桃.含脫層復合材料圓柱殼的振動模態實驗分析[J].船海工程，2010,39（4）:11-13. XIAO Hanlin,ZHOU Xintao.Experimental investigation on vibration mode of composite cylindrical shells with delamination[J].Ship&Ocean Engineering,2010,39（4）: 11-13.(in Chinese)

[10]駱志高，陳保磊，龐朝利.金屬塑料復合材料的減振性能模態實驗分析研究 [J].噪聲與振動控制，2010,（2）:

Research of Vibration Modal Experiment for Composite Laminates

QI Wen-Kai,CHENG Bo,LIU Lei
（College of Energy and Power Engineering,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China）

The modal experiment and modal identification of composite laminates with no damage and a hole damage were performed in the free state and the end fixed supported state by the method of point by point to excite and one point to test(SISO).The influence of opening damage location and damage size on the vibration performance of composite laminates was analyzed in different boundary conditions based on the modal parameters i.e. frequency,damping and modal shape.The experimental results show that composite laminates has superior damping characteristics,and its vibration characteristics are also consistent with the results in the literature.

composite laminates;modal experiment;natural frequency;damping

漆文凱（1970），男，工學博士，副教授，研究方向為航空發動機結構強度與振動。

航空科學基金（2013ZB52019）資助

2013-05-15