平面選址問(wèn)題的螢火蟲(chóng)算法

程 魁， 馬 良

（上海理工大學(xué)管理學(xué)院，上海 200093）

平面選址問(wèn)題的螢火蟲(chóng)算法

程 魁， 馬 良

（上海理工大學(xué)管理學(xué)院，上海 200093）

平面選址問(wèn)題是工程設(shè)計(jì)、線路布置、項(xiàng)目選址等工作中經(jīng)常碰到的典型組合優(yōu)化難題，根據(jù)群集智能優(yōu)化原理，給出一種基于人工螢火蟲(chóng)群優(yōu)化算法的求解方法，并針對(duì)平面選址問(wèn)題進(jìn)行求解.為避免算法陷入局部極值，將一種鄰域搜索的局部搜索方法引入螢火蟲(chóng)算法中.通過(guò)對(duì)典型平面選址問(wèn)題的仿真實(shí)驗(yàn)和與其它算法的比較，表明算法可行有效，且具良好的全局優(yōu)化能力.

平面選址；螢火蟲(chóng)群優(yōu)化算法；優(yōu)化算法

1 算法思想

GSO算法是一種新型群智能優(yōu)化算法，并在2009年成功地將其應(yīng)用在函數(shù)數(shù)值優(yōu)化問(wèn)題上.近年來(lái)，國(guó)外諸多學(xué)者已將GSO算法應(yīng)用在尋找危險(xiǎn)信號(hào)源的位置、網(wǎng)絡(luò)機(jī)器系統(tǒng)定位多個(gè)氣味源、追逐多個(gè)移動(dòng)信號(hào)源［8-9］等諸多方面.在基本的GSO算法中，每只人工螢火蟲(chóng)分布在目標(biāo)函數(shù)的定義空間內(nèi)，這些人工螢火蟲(chóng)各自攜帶自身的螢光素，并且擁有各自的視野范圍，稱(chēng)為區(qū)域決策范圍.區(qū)域決策范圍的大小會(huì)受鄰居數(shù)量的影響，當(dāng)鄰居密度較低，螢火蟲(chóng)的決策半徑會(huì)加大，以利于尋找更多的鄰居；反之，決策半徑減小.在螢火蟲(chóng)的運(yùn)動(dòng)當(dāng)中，每一只螢火蟲(chóng)以一定的概率向其鄰域范圍內(nèi)的鄰居螢火蟲(chóng)前進(jìn).螢火蟲(chóng)j要成為螢火蟲(chóng)i的鄰居螢火蟲(chóng)，必須滿(mǎn)足j在i的鄰域范圍之內(nèi)，并且j的熒光素要高于i.最終，通過(guò)螢火蟲(chóng)群的不斷運(yùn)動(dòng)，越來(lái)越多的螢火蟲(chóng)會(huì)聚集在適應(yīng)度值最高的螢火蟲(chóng)周?chē)瑥亩_定目標(biāo)函數(shù)的最優(yōu)值.

在GSO當(dāng)中每一次迭代都由兩個(gè)階段組成，第一階段是螢光素更新階段，第二階段是螢火蟲(chóng)的運(yùn)動(dòng)階段.

在熒光素更新階段中，每一只螢火蟲(chóng)對(duì)熒光素的更新式為

式中，li（t）為第t代第i個(gè)螢火蟲(chóng)的熒光素值；p為熒光素值的消失率，p∈（0，1）；γ為熒光素更新率；f（xi（t））為函數(shù)適應(yīng)度值.

在螢火蟲(chóng)運(yùn)動(dòng)階段中，螢火蟲(chóng)i以一定的概率選擇鄰域范圍內(nèi)的螢火蟲(chóng)j，并朝其運(yùn)動(dòng)，概率選擇式為

螢火蟲(chóng)i在其鄰域內(nèi)按照交叉換位策略進(jìn)行位置更新，運(yùn)動(dòng)的最后進(jìn)行決策域范圍的更新式為

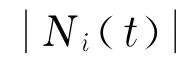
在鄰域搜索中，當(dāng)前解（x，y）鄰域定義為

其中，搜索半徑r＞0（取0.1），θ在［0，2π］之間隨機(jī)生成.由以上表述可知，求解選址問(wèn)題的人工螢火蟲(chóng)群優(yōu)化算法的步驟可概括如下：

a.初始化所有螢火蟲(chóng)的位置，鄰域范圍和相關(guān)參數(shù)值.

b.計(jì)算螢火蟲(chóng)的適應(yīng)度值.

c.利用式（1），更新螢火蟲(chóng)的熒光素值和鄰域范圍.

d.螢火蟲(chóng)在其鄰域內(nèi)按照交叉換位策略更新位置，按式（3）更新動(dòng)態(tài)決策域范圍.

e.對(duì)當(dāng)前解進(jìn)行鄰域搜索.

f.滿(mǎn)足最大迭代次數(shù)，則輸出當(dāng)前最好結(jié)果，否則，返回b.

2 仿真實(shí)驗(yàn)

為驗(yàn)證算法的運(yùn)行效果，用MATLAB7.0為算法編寫(xiě)了程序，并在PC系列機(jī)的Windows 7環(huán)境下運(yùn)行.螢火蟲(chóng)算法的參數(shù)設(shè)置采用文獻(xiàn)［10］推薦的取值，即熒光素的初值L0=5，動(dòng)態(tài)決策域初值R0=3，動(dòng)態(tài)決策域的更新率β=0.08，鄰域個(gè)數(shù)nt=5，熒光素更新率γ=0.6，熒光素消失率ρ=0.4.測(cè)試算例來(lái)源于文獻(xiàn)［3］和文獻(xiàn)［11］，如表1所示.為公平起見(jiàn)，3種算法均采用本文定義的鄰域搜索方法.

2.1 無(wú)區(qū)域約束的平面選址問(wèn)題

運(yùn)行螢火蟲(chóng)算法求解，并與當(dāng)前求解該問(wèn)題效果最好的兩種智能優(yōu)化算法——人工蜂群算法（artificial bee colony algorithm，ABC）和引力搜索算法（gravitational search algorithm，GSA）進(jìn)行求解性能比較.具體的求解結(jié)果對(duì)比如表2所示，其中，人工蜂群算法和引力搜索算法的參數(shù)設(shè)置分別參考文獻(xiàn)［5］和文獻(xiàn)［6］.3種算法的群體規(guī)模均為50，最大迭代次數(shù)N均為1 000.

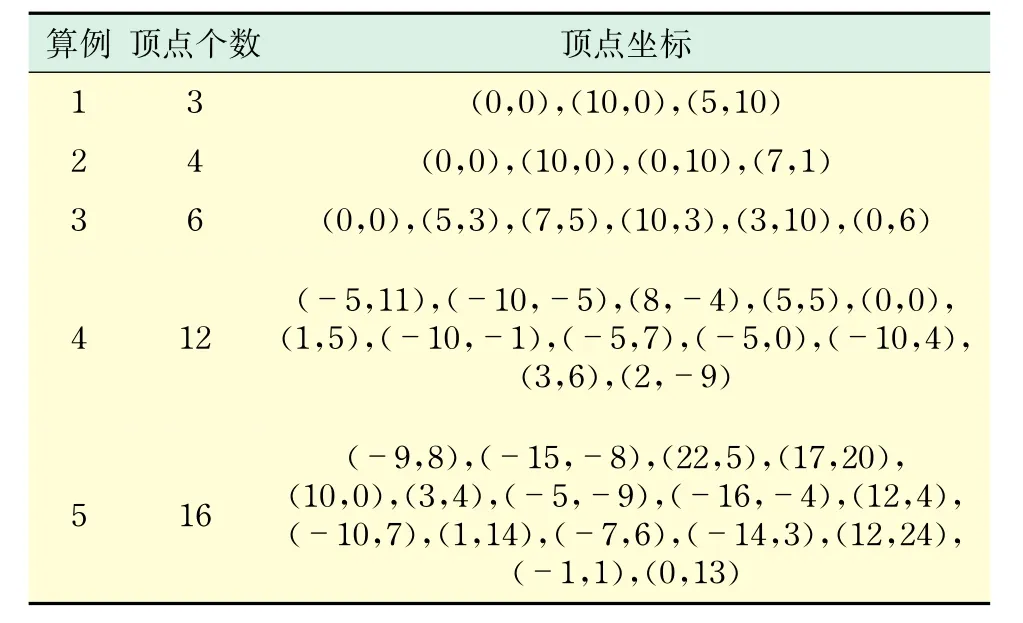
表1 測(cè)試算例Tab.1 Instances

表2 無(wú)約束情形求解結(jié)果Tab.2 Solutions under unconstrained situation

從表2可看出，在求解絕對(duì)值距離平面問(wèn)題時(shí)，對(duì)算例1和算例3而言，GSO算法的結(jié)果最好；對(duì)算例2而言，這3種算法的求解結(jié)果一樣；對(duì)算例4和算例5而言，GSO算法和GSA算法的結(jié)果一樣，都優(yōu)于ABC算法.在求解歐氏距離平面問(wèn)題選址時(shí)，對(duì)所有5個(gè)算例，GSO算法的求解結(jié)果都是最好的.總體而言，GSO算法的優(yōu)化性能要好于ABC算法和GSA算法.

為更好地說(shuō)明GSO算法在求解連續(xù)優(yōu)化問(wèn)題上的性能，選取算例3和算例5，做出3種算法求解歐氏距離最優(yōu)值的收斂性態(tài)如圖1所示（見(jiàn)下頁(yè)），無(wú)論是收斂速度還是求解精度，GSO算法都體現(xiàn)了令人滿(mǎn)意的性能.

2.2 有區(qū)域約束的平面選址問(wèn)題

為驗(yàn)證算法在該問(wèn)題上的有效性，將求解結(jié)果與蟻群算法（ant colony optimization，ACO）和人工蜂群算法（ABC）［5］的求解結(jié)果作對(duì)比.具體對(duì)比結(jié)果見(jiàn)表3（見(jiàn)下頁(yè)）.其中，算例4和算例5的區(qū)域約束分別為

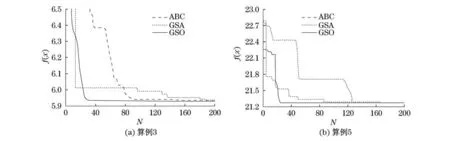
圖1 收斂性對(duì)比Fig.1 Convergence comparison

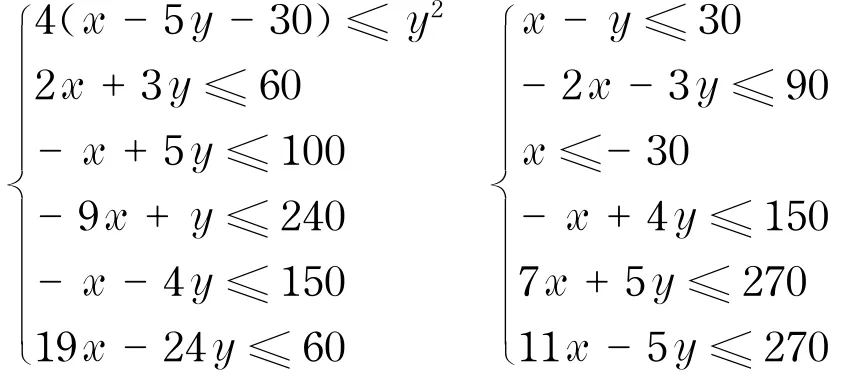
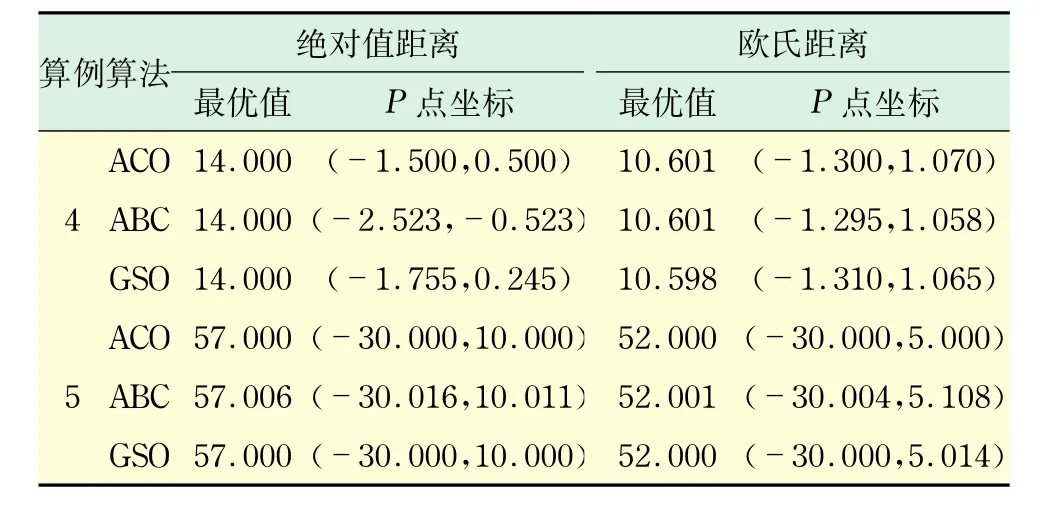
表3 有約束情形求解結(jié)果Tab.3 Solutions under constrained situation

由表3可知，對(duì)于算例4而言，在求解絕對(duì)值距離平面問(wèn)題時(shí)，3種算法求解結(jié)果一樣；在求解歐氏距離平面問(wèn)題時(shí)，GSO算法優(yōu)于其它兩種算法.對(duì)于算例5來(lái)說(shuō)，兩種形式下，GSO和ACO算法求解效果相同，均優(yōu)于ABC算法.因這類(lèi)算法出現(xiàn)時(shí)間不長(zhǎng)，理論基礎(chǔ)尚未完善，漸進(jìn)收斂性、魯棒性等性質(zhì)的嚴(yán)格數(shù)學(xué)證明尚有待于以后更深入的工作.

3 結(jié)束語(yǔ)

一系列數(shù)值試算結(jié)果表明，無(wú)論是求解無(wú)區(qū)域約束的平面選址問(wèn)題還是求解有區(qū)域約束的平面選址問(wèn)題，螢火蟲(chóng)算法都具有較為理想的收斂特性和尋優(yōu)能力，在實(shí)際操作上是行之有效的.螢火蟲(chóng)算法作為一種新型智能優(yōu)化算法，應(yīng)用領(lǐng)域還在不斷豐富，理論研究也有待探索.此外，將算法用于多目標(biāo)的平面選址問(wèn)題是下一步的研究工作.

［1］ 張?zhí)熨n.平面選址問(wèn)題概述［J］.運(yùn)籌學(xué)雜志，1985，4（1）：4-11.

［2］ 馬良.多目標(biāo)平面選址問(wèn)題的模擬退火算法［J］.系統(tǒng)工程理論與實(shí)踐，1997，17（3）：70-73.

［3］ 馬良，朱剛，寧愛(ài)兵.蟻群優(yōu)化算法［M］.北京：科學(xué)出版社.2008.

［4］ 邱模杰，馬良.約束平面選址問(wèn)題的螞蟻算法［J］.上海理工大學(xué)學(xué)報(bào)，2000，22（3）：217-220.

［5］ 樊小毛，馬良.約束平面選址問(wèn)題的蜂群優(yōu)化算法［J］.上海理工大學(xué)學(xué)報(bào)，2010，32（4）：378-380.

［6］ 劉勇，馬良.平面選址問(wèn)題的引力搜索算法求解［J］.計(jì)算機(jī)工程與應(yīng)用，2012，48（27）：42-44，62.

［7］ Krishnanand K N，Ghose D.Detection of multiple source locations using a glowworm metaphor with applications to collective robotics［C］∥Proc of IEEE Swarm Intelligence Symposium.Piscataway：IEEE Press，2005：84-91.

［8］ Krishnanand K N，Ghose D.A glowworm swarm optimization based multi-robot system for signal source localization［M］.Springer：Design and Control of Intelligent Robotic Systems，2009：53-74.

［9］ Krishnanand K N，Ghose D.Theoretical foundations for rendezvous of glowworm-inspired agent swarms at multiple location［J］.Robotics and Autonomous System，2008，7（56）：549-569.

［10］ 黃正新，周永權(quán).變步長(zhǎng)自適應(yīng)螢火蟲(chóng)群多模態(tài)函數(shù)優(yōu)化算法［J］.計(jì)算機(jī)工程與應(yīng)用，2012，48（8）：43 -47.

［11］ 蔣良奎.平面選址問(wèn)題的一種混合算法［J］.上海海運(yùn)學(xué)院學(xué)報(bào)，1999，20（4）：98-102.

（編輯：金 虹）

Artificial Glowworm Swarm Optimization Algorithm for Location Problem

CHENGKui， MALiang
（Business School，University of Shanghai for Science and Technology，Shanghai 200093，China）

The location problem is a typical combinatorial optimization problem in the work of engineering design，line routing，project location，etc.According to the principle of swarm intelligence，a new optimization algorithm based on the idea of glowworms-the glowworm swarm algorithm was presented to solve the location problem.To avoid getting stuck into local optima，a neighborhood search strategy was introduced into the artificial glowworm swarm optimization algorithm.Simulated tests of the location problem and comparisons with other algorithms show that the algorithm is feasible and effective and has strong global optimization ability.

location problem；artificial glowworm swarm optimization algorithm；optimization algorithm

O 211.1；N 94

A

1007-6735（2013）03-0205-04

2012-12-24

國(guó)家自然科學(xué)基金資助項(xiàng)目（70871081）；上海市研究生創(chuàng)新基金資助項(xiàng)目（JWCXSL1202）

程 魁（1989-），男，碩士研究生.研究方向：智能優(yōu)化.E-mail：iamchengkui＠126.com

馬 良（1964-），男，教授.研究方向：智能優(yōu)化、系統(tǒng)工程.E-mail：maliang＠usst.edu.cn