基于LDA的潛艇機械噪聲識別算法研究*
劉 杰 張福生 馮 達
(91388部隊92分隊 湛江 524022)
1 引言
目前暴露潛艇的主要特征是聲波信號。潛艇在水下的噪聲主要可以分為機械噪聲、水動力噪聲和螺旋槳噪聲,其中在潛艇常用的低速隱蔽工況下,機械噪聲通常是其水噪聲的主要來源[11~12]。所以研究潛艇噪聲源識別對于保證潛艇隱身性是至關重要的。而且,當機器出現故障時,其振動和聲信號特征一定會發生變化,所以通過對噪聲源的識別定位研究,能夠更好地對機器進行狀態檢測及故障診斷[2]。
由于潛艇機械設備異常復雜,在實際使用中,對其進行狀態檢測及故障診斷非常麻煩,一般情況下都是通過使用大量的測量傳感器對設備實行實時監測,但是傳感器各測量值之間必然存在相關性以及隨機誤差的影響,在使用中極不方便[6~8]。基于統計理論的線性判別分析算法(LDA)和主成分分析算法(PCA)[1],通過對大量樣本數據進行分析建模,克服了傳統的基于機理模型的監測診斷方法的缺點[3,11]。
線性判別分析算法是基于Fisher準則尋找一組將高維樣本投影到低維空間的最佳的判別投影向量,使所有的投影樣本類內離散度最小且類間離散度最大。主成分分析算法就是使用較少的綜合變量來代替原始數據中較多的變量,綜合變量之間互不相關,從而減少變量之間的冗余,同時最大限度的保持原始數據的信息。LDA算法是直接以分類為目的的特征提取方法,所以在噪聲的分類識別中要優于PCA算法。
在直接使用LDA算法進行噪聲特征提取的時候可能存在小樣本問題,導致無法建立正確的噪聲識別模型,所以本文先采用PCA對樣本進行降維,再使用LDA進行模型的建立[4~5]。建立模型后,通過將待測信號投影到模型空間上,再與已有的數據樣本庫進行比較,確定噪聲信號類別,達到狀態檢測及故障診斷的目的。
2 主成分分析
PCA是1901年由Pearson提出的一種多變量統計分析技術,是一種最優的正交線性變換,能夠將信號數據在一個較低維的空間進行處理,目前廣泛應用于信息壓縮。
設樣本信號集X=(x1,x2,…,xN),xi(i=1,2…,N)表示X中第i個信號向量,N表示樣本數目,M表示xi的維數。求解X的總體散度矩陣ST:
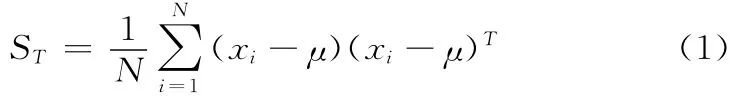
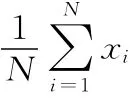
使用奇異值分解方法求解ST的特征值λi(i=1,2,…,M)及其對應的特征向量(主元)φi(i=1,2,…,M)。λi值的大小是按降序排列,即λ1≥λ2≥…≥λM,λi值越大表示對應的主元φi的貢獻度越大。
主元數目n(n≤M)通過交叉檢驗法或主元貢獻率累積和百分比ξ(CPV)的方法確定。本文采用CPV方法,其中ξ=0.9,取使式(2)成立的最小值L為n:

最后確定的主元組成的矩陣就是PCA投影子空間WPCA= (φ1,φ2,…,φn)。
3 線性判別分析

圖1 PCA和LDA對兩類問題投影子空間求解的比較[1]
LDA的原理就是尋找一個投影方向,所有樣本在這個方向的投影能夠實現類間離散度最大化和類內離散度最小化,即能夠使同類樣本盡量聚集,不同類樣本盡量分開。LDA是以分類為目的的特征提取方法,所以在識別分類別中要優于PCA,圖1給出了PCA和LDA分別在兩類問題上求解投影子空間的情況。
從中可以看出,經過LDA投影后的子空間分類能力明顯好于經PCA投影后的子空間。
因為LDA使用的是Fisher準則函數,所以LDA也稱為Fisher線性判別分析Fisher準則函數為

樣本類間離散度矩陣Sb定義為


樣本的類內離散度矩陣Sw定義為


如果Sw是非奇異的,投影矩陣WLDA定義為

WLDA=w{i|i=1,2,…,}m相當于通過式(7)求解:

其實質就是求解S-1wSb的特征值問題,WLDA= {wi|i=1,2,…,m}就是由最大的m(m≤n)個特征值對應的特征向量組成,n表示樣本維數,m表示WLDA的投影維數,m的大小一般通過實驗確定。
當N≥n時,即樣本的數量不小于樣本的維數時,Sw是非奇異的,但是在N<n時,Sw很可能是奇異的,這樣就無法對Sw求逆,即存在小樣本問題。為了克服這種缺陷,本文先使用PCA對原始樣本集進行降維,從而保證Sw的非奇異性。
4 算法模型
圖2給出了使用線性判別分析算法進行噪聲識別的整個流程。
設:
l為測量傳感器的個數;
ai(i=1,2,…,l)為第i個測量傳感器測量的參數個數;
m為每一個樣本信號的維數,m=a1+a2+…+al;
n為潛艇機械噪聲源的個數;
ki(i=1,2,…,n)為第i個機械噪聲源包含的信號數量(不同工況下的信號);
N:樣本信號的數量,N=k1+k2+…+kn。
噪聲訓練樣本集X∈RN×m,首先根據式(1)和式(2)確定WPCA矩陣,對WPCA矩陣進行LDA運算,得到WLDA矩陣,最后得到算法模型矩陣W=WTPCA·WTLDA。

圖2 基于LDA的噪聲識別流程圖
得到算法模型后,再將待測信號與已知信號庫(機械設備正常工況下的噪聲信號和所有已知故障情況下的噪聲信號)中所有信號分別投影到識別分類模型上一一進行相似度計算和比對,最后根據相似度的大小確定待測信號的類型,從而達到噪聲源的定位和故障診斷的目的。
相似度的計算可以采用歐氏距離、馬氏距離和歸一化互相關系數(Normalized Cross-Correlation,NCC)等方法。本文使用NCC計算相似度δ,計算公式如下:
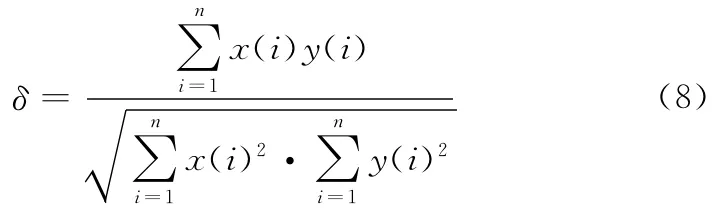
x和y表示兩個不同的信號向量,n表示向量的維數,0<δ≤1表示互相關系數,即相似度,當x=y時,δ=1,表示兩個完全相同的特征向量。δ越大表示兩個信號的相關性越大。
5 實驗結果與分析
利用四臺機械設備模擬潛艇噪聲源,通過改變設備的工況來模擬機械的故障噪聲,每臺設備使用四種不同的工況,共采用五個測量傳感器,每一個傳感器取四個參數作為特征值,這樣組成的訓練樣本集為16×20的矩陣。采用另外四臺機械設備,每臺設備使用十種不同工況模擬待測噪聲信號。實驗結果如圖3所示。m表示LDA模型的投影維數,P表示在不同m下的模型識別率:

從結果看,剛開始P隨著m的增加有明顯的提升,當m=6時P取得最大值0.825,隨著m的進一步增加,P有所下降,但趨于穩定,這是因為LDA是一種提取信號分類特征信息的算法,m值越大,會引入其他的干擾信息,m值過小,則不足以提取足夠的分類信息。

圖3 LDA模型識別率與投影維數的關系
通過改變訓練樣本集中機械設備的數量和每臺設備使用的工況數量進行實驗,測試影響LDA算法模型識別分類效果的主要因素。實驗結果如圖4和圖5所示。
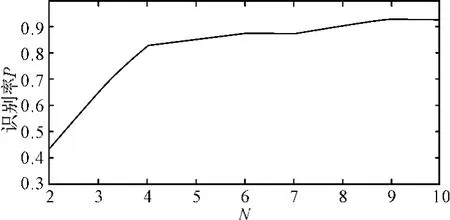
圖4 LDA模型識別率與訓練集機械設備數量的關系

圖5 LDA模型識別率與訓練集每臺設備使用的工況數量的關系
N表示訓練集機械設備的數量,K表示訓練集每臺設備使用的工況數量,其中在圖4中K=4;圖5中N=4;從實驗結果可知識別率P與N和K成正相關關系,在N或K達到一定值后,P都會趨于穩定。在所有實驗中LDA模型的投影維數m都是取最優值。
6 結語
使用LDA算法得到的算法模型一旦確定后,可以將其存儲起來,在以后的使用中直接進行調用,不需要重新計算,使用比較方便。LDA的實質是一種以分類為目的的特征提取方法,其模型的生成與訓練樣本信號的類型沒有本質的聯系,所以,使用其他信號(比如水面艦噪聲信號等)建立的算法模型,也可以用于潛艇的機械噪聲信號識別中,具有較好的通用性。
從實驗中可以看出,LDA模型的分類識別能力主要受到訓練樣本集規模的影響,樣本集中信號類別數越多(即噪聲源越多)以及每一個噪聲源包含的信息類型越多,在計算LDA類間協方差矩陣和類內協方差矩陣的時候就能夠得到更多的分類信息,其分類識別能力就越強。此外,在實際使用中,已知信號庫中不可能包含每臺機械設備噪聲源的所有故障信息,從而影響實際的使用效果,所有,下一步的研究重點是需要在模型中加入拒識功能,提高算法的分類識別能力。
[1]A.M.Martinez and A.C.Kak.PCA versus LDA[J].IEEE Trans.On Pattern Analysis and Machine Intelligence,2001,23(2):228-233.
[2]高明杰,呂志強,章林柯.多元統計分析在潛艇噪聲源識別中的應用[J].船海工程,2009,38(1):93-97.
[3]邊肇棋,張長水,張學工.模式識別[M].北京:清華大學出版社,2000:87-112.
[4]章林柯,崔立林.潛艇機械噪聲源分類識別的小樣本研究思想及相關算法評述[J].船舶力學,2011,15(8):940-947.
[5]楊德森.水下航行器噪聲分析及主要噪聲源識別[D].哈爾濱:哈爾濱工程大學,1998:13-26.
[6]姚耀中,林立.潛艇機械噪聲控制技術綜述[J].艦船科學技術,2007,29(1):21-26.
[7]余桐奎.基于多輸入/輸出模型的噪聲源分離方法研究[D].哈爾濱:哈爾濱工程大學,2009:10-21.
[8]孔建益,李公法,侯宇.潛艇振動噪聲的控制研究[J].噪聲與振動控制,2006:1-4.
[9]施引,朱石堅,何琳.艦船動力機械噪聲及其控制[M].北京:國防工業出版社,1990:122-147.
[10]劉萍,廖廣銳.高噪聲背景下的語音識別系統設計[J].計算機與數字工程,2009(7).
[11]方開泰.實行多元統計分析[M].上海:華東師范大學出版社,1986:54-71.
[12]俞孟薩,黃國榮,伏同先.潛艇機械噪聲控制技術的現狀與發展概述[J].船舶力學,2003,7(4):110-120.

