一種弧齒錐齒輪行星傳動齒輪箱體的模態分析

魏冰陽，周 賀，陳金瑞

(河南科技大學機電工程學院，河南洛陽471003)

0 引言

齒輪箱作為機械設備傳遞動力的重要部件，工作時受到內部或外部的激勵會產生較大的振動。這些振動都會以不同的形式傳遞到箱體上，箱體劇烈振動或者損傷會反過來嚴重影響齒輪箱的整體使用壽命，因此，在齒輪箱設計中對箱體的剛性指標有很高的要求[1］。齒輪箱的動態設計要求箱體具有良好的動態特性(固有頻率和振型)。目前，國內外廣泛利用有限元模態分析方法識別齒輪箱的模態參數，為齒輪箱體的結構優化設計提供重要的手段[2-6］。模態分析是研究結構動力特性的一種方法，是系統識別方法在工程振動領域中的應用[7］。文獻[8］基于UG NX平臺建立了齒輪箱體有限元分析模型，得到了固有頻率和振型之間的關系，通過增加箱體加強筋的方法使得結構變形減小，達到減震降噪的目的。文獻[9］利用ANSYS分析模態振型對箱體性能的影響，通過增加壁厚優化箱體，達到減小變形，降低振動的目的。本文擬對一種新型弧齒錐齒輪行星傳動的齒輪箱體進行有限元模態分析[10］，通過對固有頻率和振型的分析提出改進意見，避免發生共振，為箱體減振、降噪提供重要的依據。

1 錐齒輪行星傳動箱體結構的選擇

圖1為新型弧齒錐齒輪行星傳動原理結構圖[11-12］，在傳動過程中，當太陽輪1作為輸入傳動時，行星輪2被動，由于行星輪2的軸與行星架H固聯，支撐輪4與箱體固聯，而行星架H是浮動的，所以行星輪2在自轉的同時還圍繞太陽輪1公轉。同理，行星輪3在自轉的同時，也圍繞支持輪4公轉。當中心輪1、4的齒數差為正整數時為增速傳動，反之為減速傳動。對于新型弧齒錐齒輪行星傳動箱體設計，文獻[12］中采用了傳統的上下結合的方形箱體結構，這種結構形式雖然在強度、剛度方面具有一定的可靠性，但是箱體質量大，材料浪費較多。另外，這種結構形式也不方便采用法蘭直聯。鑒于此，本文設計了一種大弧面箱體結構，這種類似于軸承座的弧面結構與方形箱體相比具有如下優點:(1)可設計成底面坐聯或者法蘭盤直聯結構。(2)提高了箱體抗振能力和箱體的基頻頻率，同等條件下減小了箱體的質量和體積。(3)與回轉行星架相適應，攪油、散熱均勻。

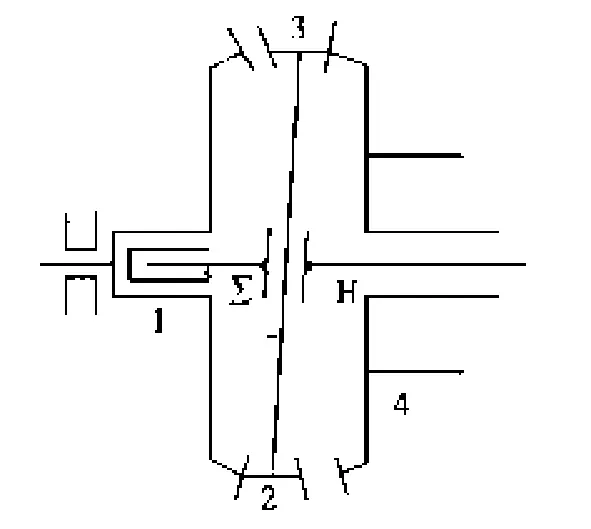
圖1 錐齒輪行星傳動原理圖

2 齒輪箱體有限元模型的建立

2.1 齒輪箱體模型的建立與簡化

根據新型弧齒錐齒輪行星傳動的要求，基于CATIA建立齒輪箱體的三維模型，箱體采用徑向剖分式，由左、右兩部分組成。箱體上方有窺視孔、吊耳、凸臺、圓角及螺栓的連接等細小組件結構，由于這些細小結構部分對箱體模態分析影響不大[13］，劃分網格時會產生數以千計的節點和單元，大大增加計算機的數據處理量，有可能造成奇異解，無法分析，因此，在建立箱體模型時對箱體的部分細小結構采取了一些簡化措施[14］。運用CATIA建立的新型弧齒錐齒輪箱體三維模型如圖2所示。采用底面支承結構，兩端面設置軸承座孔。

2.2 齒輪箱體有限元模型的建立

通過ANSYS中的impot將CATIA中建立的箱體三維模型導入到ANSYS中，在單元選擇時，選用對結構復雜性適應性較好的四節點四面體solid187單元進行網格劃分，然后利用ANSYS中的check mesh功能對錯誤的單元進行檢查，再利用creact element重建單元。建立的齒輪有限元模型見圖2。

2.3 齒輪箱體材料屬性的確定

齒輪箱體材料選擇性價比高的鑄鐵HT250，根據《機械設計手冊》[15］，其泊松比 μ=0.27，彈性模量 E=1.55×105MPa，密度 ρ=7.0 ×10-6kg/mm3。

2.4 邊界條件的確定

邊界條件的施加與工程實際條件是否吻合，將直接影響到計算結果的正確性與合理性，如果箱體按照實際施加邊界條件當然能更好地反映箱體的動態性能，但由于實際情況極其復雜，實際邊界剛度較大，在進行分析時可能造成矩陣病態，嚴重時對計算精度影響很大，因此很難做到與實際完全相符。模態分析時有限元模型是建立在靜態分析的基礎上的，進行齒輪箱體模態分析時求的是傳動的固有特性，與所受的外力無關，故可不考慮外部載荷的作用。

這里齒輪箱體按照地腳螺栓固定形式設計，為了更好地反映實際情況在底面上使用完全約束，使其沒有移動及旋轉自由度，相當于箱體地面完全固定。

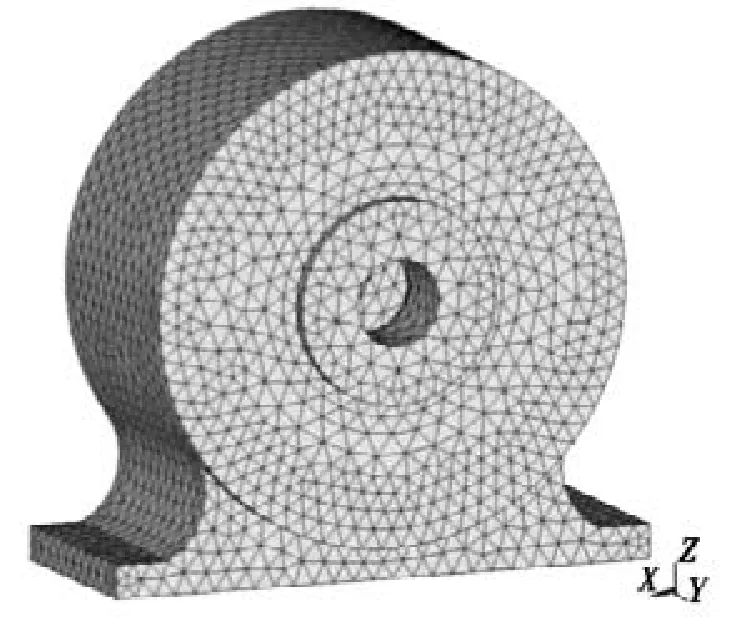
圖2 新型弧齒錐齒輪有限元模型

3 齒輪箱體的有限元模態分析

3.1 對箱體的模態結果進行分析

本文對新型弧齒錐齒輪箱體的有限元模態分析采用約束模態計算，ANSYS提供了7種模態提取方法，求解時根據模型的實際情況加以選擇，通過具體的比較分析，本文采用ANSYS默認的Block Lanczos(分塊蘭索斯)法進行求解，該方法對計算機內存要求較高，主要提取多階的模態，求解的時間較短，適用于大型特征值求解問題。系統的第i階振型固有頻率[16］可由下式求出

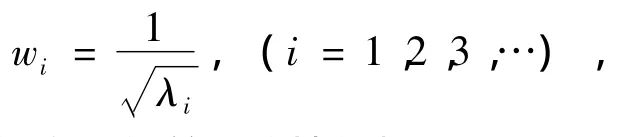
式中，w為系統的固有頻率;λ為特征方程的第i階特征根。

在對齒輪箱體模態的提取時不必求出全部的固有頻率及振型，因為低階振型對結構振動的影響遠高于高階振型，因此，低階振型決定了結構的振動特性，故提取了前10階固有頻率及對應振型。振型特征(限于篇幅只給出前6階振型)如圖3所示，固有頻率如表1所示。

通過對弧齒錐齒輪箱體振型及動畫顯示可知:

(1)第1階模態以輸入輸出軸方向來回擺動，可以看出箱體的上部變形較大。

(2)第2階模態以箱體底座為中心，沿垂直于輸入輸出軸的方向來回擺動，和第1階振型相似箱體的頂部變形較大。

(3)第3階模態繞Z軸以箱體底座為中心整體扭轉，這樣的扭轉振動容易引起齒輪的不對中，造成齒輪接觸變差，影響齒輪的壽命，最大變形量出現在與箱體底座長度方向平行的箱體兩側。

(4)第4階箱體模態振型以輸入輸出軸方向的箱體兩側面來回擺動，箱體的輸入端變形明顯大于其他部位。

(5)第5階箱體模態振型以輸入輸出軸方向整個箱體變形較明顯，其中輸出端口變形較大。

(6)第6階箱體的模態以底座為基面箱體上下振動，箱體的頂部變形較明顯。

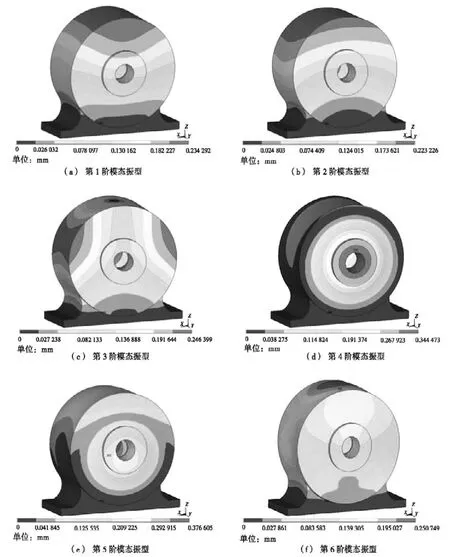
圖3 新型弧齒錐齒輪箱體前6階振型結果

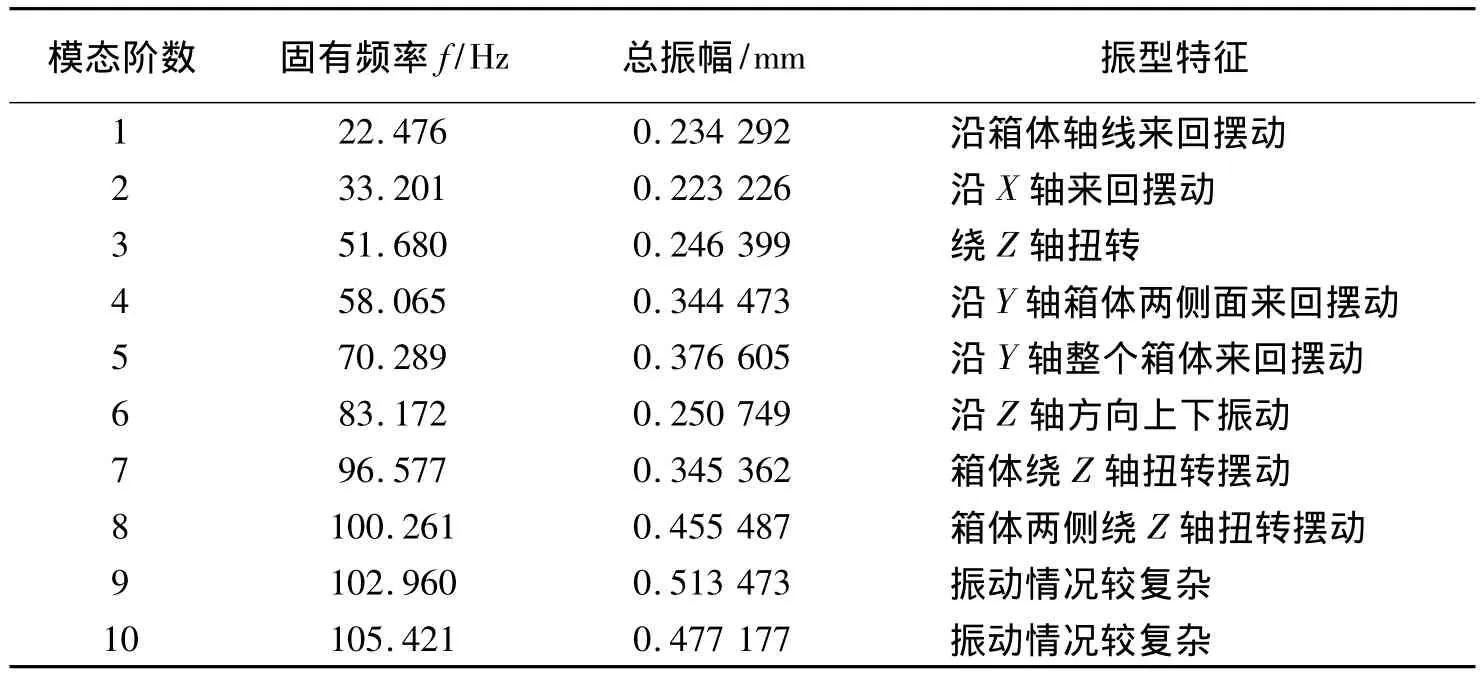
表1 新型弧齒錐齒輪箱體固有頻率及振型結果

3.2 齒輪箱體的改進方案

(1)從對箱體振型的分析結果來看，箱體的兩側、頂部及其輸入輸出端口變形量較大，可以通過增加壁厚及增加箱體頂部凸臺的厚度來增加其剛度，以減小變形量，提高固有頻率。

(2)可以通過在箱體上側及軸承端口處設置加強筋來提高剛度，以減小變形，提高固有頻率。

3.3 齒輪箱體改進后模態參數

由上面對弧齒錐齒輪箱體模態的分析可知:振動的位移對箱體的影響較大，通過對箱體改進后的分析提取的模態參數如表2所示。

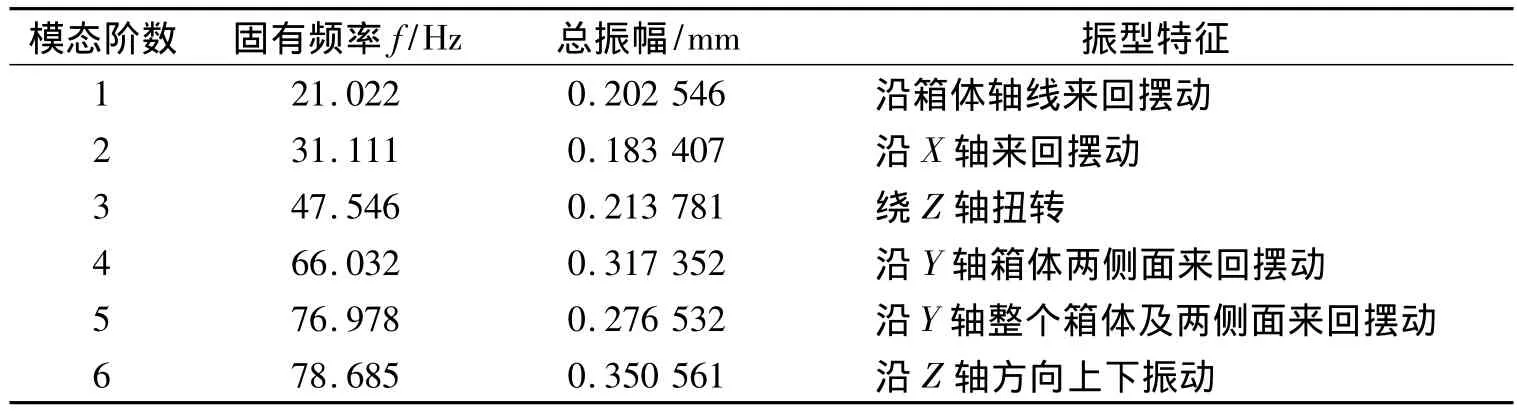
表2 新型弧齒錐齒輪箱體改進前后固有頻率及變形量對比

由表2可知:優化后的結構的變形量有明顯的減少，穩定性有所提高，能夠更好的適應因變形對箱體造成的不良影響。

4 結論

在CATIA中建立了新型弧齒錐齒輪行星傳動箱體的三維模型，導入ANSYS進行了模態分析，為齒輪箱體的優化設計提供了依據。在方便齒輪系統裝配的條件下，箱體采用了弧面結構，有效減小了箱體的質量，提高了箱體固有基頻的頻率，減少了齒輪箱體模態頻率出現的次數。找出了齒輪箱體的薄弱環節，通過增加壁厚、箱體頂部凸臺，上側及軸承端口處設置加強筋，能夠提高齒輪箱的整體剛度，減小變形，提高其固有頻率。

[1]丁康，李魏華，朱小勇.齒輪及齒輪箱故障診斷實用技術[M］.北京:機械工業出版社，2005.

[2]傅志方，華宏星.模態分析理論與應用[M］.上海:上海交通大學出版社，2000.

[3]楊成云.中心傳動齒輪箱體有限元分析及結構優化設計[J］.重型機械，2001(2):42-44.

[4]盛和太，喻海良，范訓益.ANSYS有限元原理與工程應用實例大全[M］.北京:清華大學出版社，2006.

[5]劉國慶，楊慶北.ANSYS工程應用教程機械篇[M］.北京:中國鐵道出版社，2003.

[6]劉東超，楊宏斌.基于加工的弧齒錐齒輪三維建模[J］.河南科技大學學報:自然科學版，2010，31(5):12-15.

[7]李瑞虎，王凱，謝國燦.基于ANSYS的平面凸輪有限元模態分析[J］.機械傳動，2006，3(6):61-63.

[8]林雪妹，童水光，童小紅，等.大型船用齒輪箱的模態分析及結構優化[J］.機械設計與制造，2011(11):175-176.

[9]張學亮，程珩，趙遠.基于ANSYS技術的齒輪箱模態分析及優化[J］.機械工程師，2010(6):70-72.

[10]巫山，孫華，周文.減速機齒輪的模態分析和研究[J］.機械，2010，37(9):20-21，24.

[11]魏冰陽，楊建軍，鄧效忠，等.一種錐齒輪行星傳動機構:中國，2011201038987[P］.2011-4-11.

[12]彭宗和.新型弧齒錐齒輪行星傳動的嚙合性能與試驗[D］.洛陽:河南科技大學，2011:1-55.

[13]崔振家，汪鴻振.ANSYS的前傳動系統模態分析[J］.噪聲與振動控制，2007(6):36-38.

[14]朱才朝，徐向陽，王海霞，等.大功率船用齒輪箱結構優化[J］.重慶大學學報，2008，31(11):1221-1225.

[15]機械設計手冊編寫組.機械設計手冊[M］.北京:北京工業出版社，1997.

[16]馬小明，劉志偉.基于ANSYS的大型不銹鋼閥體有限元分析[J］.現代制造工程，2011(3):54-57，96.