高速公路收費站設計中的排隊論模型分析

劉維維，雷 博，馬偉思，黃澤濱

(1.中交第一公路勘察設計研究院有限公司;2.長安大學)

高速公路收費站設計中的排隊論模型分析

劉維維1，雷 博2，馬偉思2，黃澤濱2

(1.中交第一公路勘察設計研究院有限公司;2.長安大學)

針對高速公路收費站設計不合理導致交通擁堵、安全問題，通過對M/M/n和M/M/1排隊理論的分析，結合高速公路收費系統的特點，建立了用于高速公路收費站臺設計的排隊論模型。該模型給出了高速公路收費亭數目設計的理論依據，從而提供了一種解決收費站設計的合理方法。同時，運用Visual Basic 6.0程序進行了編程，給出了在一定服務水平條件下，不同收費亭可以服務的交通量。

高速公路;收費站設計;排隊論;模型

1 前言

隨著國民經濟的快速發展，人們的生產生活節奏越來越快，這就要求交通為人們提供一個快捷和安全的出行平臺。雖然高速公路能夠解決這一問題，但其存在的各種問題依然嚴重影響著人們的出行，尤其收費站問題。在高速公路的設計中，如果收費站的規模設置的不合理，會造成嚴重的交通擁堵、安全問題。在交通高峰期，收費站經常出現擁擠現象，甚至車輛在收費廣場內多次變換車道、搶占收費車道，大大增加了車輛間發生交織和沖突的幾率。因此，如何合理的設置收費站收費亭的個數，如何根據車流大小決定收費亭的開啟數量，是高速公路收費站設計和管理的重點問題。

排隊論(Queuing Theory)，是研究系統隨機聚散現象和隨機服務系統工作過程的數學理論和方法。高速公路收費系統，是一個典型的排隊系統。而高速公路收費站存在的問題就是沒有處理好排隊收費問題，造成擁堵。本文從排隊論基本理論出發，探討高速公路收費站收費系統設計的優化問題。

2 收費站設計中的排隊論模型建立

圖1為一最簡單的排隊系統模型。排隊系統包括三個組成部分:輸入過程、排隊規則和服務機構。

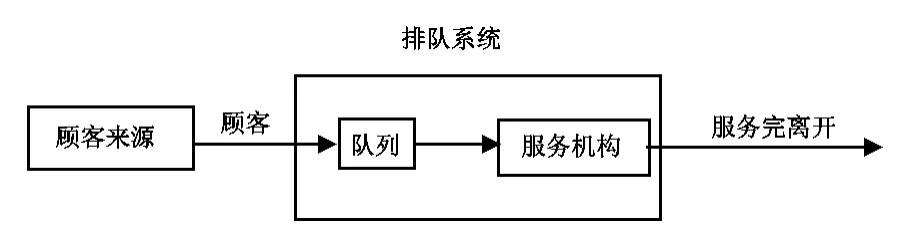
圖1 排隊論模型示意圖

輸入過程考察的是顧客到達服務系統的規律。它可以用一定時間內顧客到達數或前后兩個顧客相繼到達的間隔時間來描述，一般分為確定型和隨機型兩種。隨機型的輸入是指在時間t內顧客到達數 n(t)服從一定的隨機分布。如服從泊松分布，則在時間t內到達n個顧客的概率為

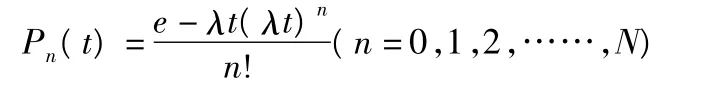
排隊論中相繼到達的顧客的間隔時間T服從負指數分布，即

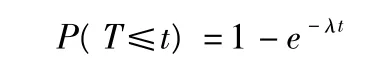
上面兩式中λ為單位時間顧客期望到達數，稱為平均到達率;1/λ為平均間隔時間。在排隊論中，討論的輸入過程主要是隨機型的。

排隊規則分為等待制、損失制和混合制三種。這里運用的排隊規則是屬于等待制，即當顧客到達時，所有服務機構都被占用，則顧客排隊等候。

服務機構可以是一個或多個服務臺。多個服務臺可以是平行排列的，也可以是串連排列的。服務時間一般也分成確定型和隨機型兩種。而隨機型服務時間v則服從一定的隨機分布。一般采用負指數分布，其分布函數是

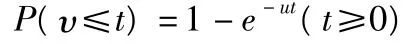
式中:μ為平均服務率，1/μ為平均服務時間。

服務機構排隊系統問題的求解。

研究排隊系統問題的主要目的是研究其運行效率，考核服務質量，以便據此提出改進措施。通常評價排隊系統優劣有6項數量指標。

(1)系統負荷水平ρ:它是衡量服務臺在承擔服務和滿足需要方面能力的尺度;(2)系統空閑概率P0:系統處于沒有顧客來到要求服務的概率;(3)隊長:系統中排隊等待服務和正在服務的顧客總數，其平均值記為LS;(4)隊列長:系統中排隊等待服務的顧客數，其平均值記為Lg;(5)逗留時間:一個顧客在系統中停留時間，包括等待時間和服務時間，其平均值記為WS;(6)等待時間:一個顧客在系統中排隊等待時間，其平均值記為Wg。

高速公路上的車輛陸續到達收費站，排隊等候，依次接受收費服務，然后離開收費站。如果到達的車輛不能及時得到服務，就產生了排隊現象，高速公路收費系統，是一個典型的排隊系統。該收費站系統采用標準的 M/M/C/∞/∞/FCFS的排隊模型。

上述符號中第一個M為車輛到達時間間隔，高速公路上的交通量較城市道路要小，可以用泊松分布描述車輛的到達，用負指數分布描述車輛到達的時間間隔;第二個M為收費服務時間，根據調查研究，該服務時間滿足正太分布，一般的統計結果為8 s;C為收費站收費亭個數;理想狀態假設:系統能容納無限多個車輛，道路上的車源也是無限的;FCFS為系統采用先到先服務的規則。

在收費站排隊系統中，車輛排隊方式是多路排隊多通道服務:指每個通道各排一個隊，每個通道只為其相對應的一隊車輛服務，車輛不能隨意換隊。當C值取1時，即為單路排隊單通道服務系統，表示只有一個收費窗口的收費系統，所以，多路排隊多通道服務系統相當于多個M/M/1單通道系統組成的排隊系統。

在收費站排隊模型中，相關符號定義如下:λ為系統中車輛為n時的平均到達強度(到達強度以單位時間內到達的車輛數表示);μ為系統車輛數為n時收費員平均(期望)服務強度(服務強度以單位時間內服務的車輛數表示);Pn為系統在時刻t有n輛車的概率;C為系統收費亭數目。

系統中主要研究和計算的數量指標有:L為系統期望車輛數，亦稱隊長;Lq為系統期望排隊車輛數，亦稱排隊長;W為車輛在系統內的期望停留時間;Wq為車輛在系統內的期望等待時間。

3 單通道服務模型M/M/1模型建立

(1)單通道服務時，模型如圖2所示。設車輛平均到達率為λ(輛/h)，系統平均服務率為μ(輛/h)，交通強度或服務程度為ρ。則

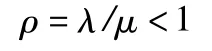
由遞推公式，系統中有n輛車的概率為

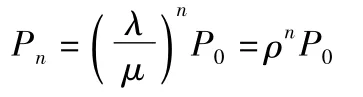
由概率性質知

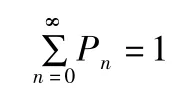
從而有

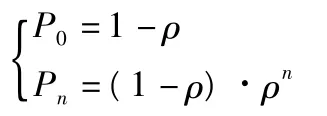
圖2 單通道服務模型

(2)系統中的隊列長度L——期望車輛數

根據系統中有n輛車的概率Pn，可知系統中的隊長L為

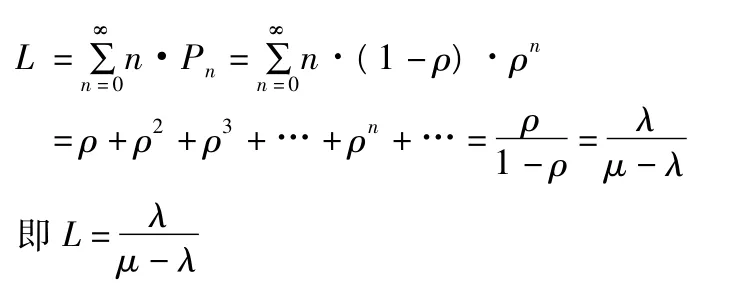
(3)系統的排隊長Lq——系統中等待的平均車輛數

(4)車輛在系統內的期望停留時間W

車輛在收費站排隊系統中的期望逗留時間W是隨機變量，可以證明，它服從參數為μ-λ的負指數分布，分布函數和密度函數為

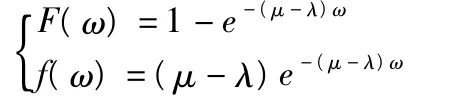
(5)車輛在系統內的期望等待時間Wq

車輛在系統內的期望等待時間Wq應該為期望停留時間W減去平均服務時間，即

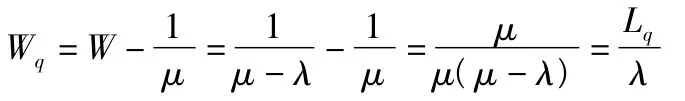
4 多通道服務模型M/M/n模型建立

由于多通道服務模型即M/M/n模型相當于多個M/M/1模型，因而在計算多通道模型時，只需計算其中一個M/M/1模型，然后乘以收費亭數即可，在復雜交通情況下可以適當乘以修正系數。

5 模型應用分析

在收費站排隊模型中，如果P＜1，則系統穩定;如果P＞1，系統的排隊長度將會無限增大，出現“爆炸”現象，因此要調整平均服務強度μ，使滿足條件是λ＜μ，保持穩定狀態即確保排隊能夠消散，在收費系統中就是能夠使排隊車輛在一定時間里面通過收費站，從而保證交通的流暢;如果系統是穩定的，但排隊和等待時間很長，也要調整平均服務強度，使其排隊長和等待時間在預定的期望值內。

高速公路收費站服務等級可根據下表服務區等級劃分標準確定，一般情況下采用二級服務標準，即排隊車輛不大于4輛。

表1 服務區等級劃分標準

對于人工收費站，服務時間根據以往經驗，取8 s，每個收費窗口的平均服務率μ0=3 600/8=450輛/h。根據3節中公式，運用Visual Basic 6.0程序編寫程序，計算不同收費亭數時的服務水平，即服務小時交通量，見表2。

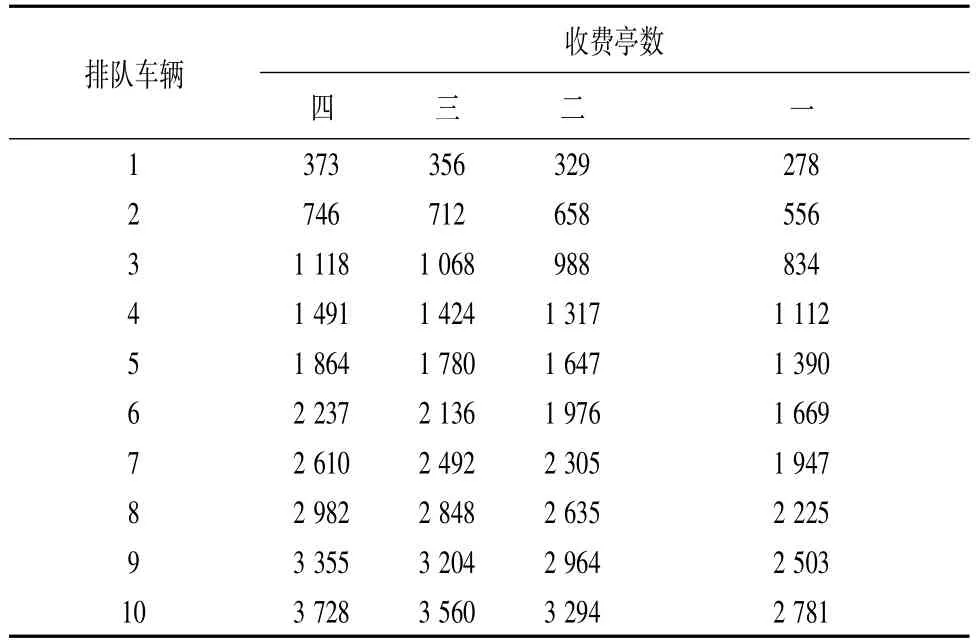
表2 不同排隊車輛時不同收費臺的服務小時交通量

(1)在進行公路收費站設計時，根據預測高峰小時交通量以及所需的服務水平，根據當地的實際情況，通過上表選擇所需的收費亭數量。

(2)在實際運營階段，根據當地某固定時段的車流量的大小，通過上表選擇需要開放的收費亭數，從而降低資源的消耗，達到節約能源的目的。

6 總結

此模型建立的目的之一是確定高速路上同一地點的最優收費亭數C和單位時間服務車輛數的能力。可以根據道路預測交通量推測平均車輛到達率λ，根據每個收費窗口服務一輛汽車的平均時間t計算系統平均服務率μ(人工停車收費系統取t=8 s，智能收費系統根據實際服務時間取值)，利用2節中公式計算隊長、排隊長、等待時間等，進而求得所需的收費亭數，也可根據不同時段公路上的交通狀態確定不同時段收費站服務臺窗口的數目，從而降低收費站服務臺的運營成本。

本文利用系統工程理論中的排隊論的基本原理，結合高速公路收費站系統的特殊性要求，建立收費站收費亭數目設計的排隊論模型，給收費站收費亭數量的確定提供了一個解決方案。同時可以利用本模型，進行收費站通行能力分析。

［1］《運籌學》教材編寫組.運籌學［M］.北京:清華大學出版社，2005.

［2］湯洪波，劉向遠，等.排隊論在公路收費站服務臺設計及管理中的應用［J］.四川建筑，2009.

［3］黃臨娜.排隊論在成渝高速公路收費站服務臺設計和管理中的應用［J］.交通標準化，2007.

［4］張政.排隊論在高速公路收費系統中的應用［J］.西安航空技術高等專科學校學報，2006.

U492

C

1008-3383(2013)04-0184-02

2012-12-05