飛機撞擊反應堆安全殼的有限元分析

李亮，潘蓉，朱秀云

(環境保護部核與輻射安全中心，北京市 100082)

0 引言

美國“9·11”恐怖襲擊引起了公眾對于現代大型飛機撞擊包括核電廠在內的國家重要基礎設施和建筑物的關注。國外核電行業進行了大量研究，以評估和提高當今核電廠承受和抵抗飛機蓄意撞擊的能力。美國核管會(nuclear regulatory commission，NRC)在“9·11”后要求美國國內核電廠對抵抗大型商用飛機的惡意撞擊進行評估。NRC通過標準“Consideration of Aircraft Impact for New Nuclear Power Reactor Designs”，并于2009年6月將大型商用飛機撞擊作為核電廠超設計基準事件考慮的規定，以美國聯邦法規新條款的形式頒布，規定2009年7月13日之后頒發證書的核動力堆的標準設計，均應對設施遭受大型商用飛機撞擊進行專門的設計評價。目前，我國的核安全法規還沒有針對大型飛機撞擊評價提出相關要求，但是建立和完善相關法規勢在必行，環保部核與輻射安全中心在這方面的研究工作也已起步。本文采用HAD101/04《核電廠廠址選擇的外部人為事件》［1］提供的波音707－320撞擊荷載函數，考慮小型商業飛機撞擊安全殼外殼的整體結構響應，分析其抵抗小型商業飛機撞擊的能力。

1 計算模型

1.1 安全殼描述

本文研究的核電廠采用第三代先進技術，其安全殼分為內外雙殼，內外殼的凈間距為1.5 m。本文的研究對象實際是安全殼的外殼，安全殼外殼作為抵抗外部事件的主要屏障，對安全殼內殼的功能防護起著重要作用，在飛機撞擊情況下保證反應堆安全停堆和放射性泄漏不超過允許值。

1.2 撞擊的基本假定

假定飛機主要由機身和機翼組成，將其等效荷載曲線作用在相應的撞擊位置。并假定飛機撞擊過程中接觸面內作用力是均勻分布的。在進行飛機撞擊分析時最不利的情況，飛機撞擊的角度選取能包絡所有情況的角度。

1.3 計算軟件及幾何模型

本文研究采用大型通用有限元程序LS-DYNA。LS-DYNA是結構撞擊分析領域最著名的軟件之一，其優勢在于可采用顯示時間積分，通過多種接觸－撞擊算法來處理高度非線性、大變形接觸和動力響應問題。

本文鋼筋模型和混凝土模型采用分離建模。混凝土采用實體單元Solid164模擬，鋼筋采用梁單元Beam161模擬，鋼筋布置在混凝土墻體內側，不考慮兩者之間的滑移，鋼筋與混凝土單元采用耦合約束(constrained_lagrange_in_solid)［2］方式。其中鋼筋模型，按照內外2層的方式布置在混凝土結構內部，鋼筋的直徑和間距按照等面積來進行折算替換，以減少鋼筋的布置密度和單元數目，提高建模的效率和計算的效率。同時，為了簡化計算模型，對安全殼進行了適當簡化，對于底部貫穿件孔洞，由于洞口尺寸不大，且離撞擊位置較遠，在幾何模型中沒有考慮這部分孔洞。另外安全殼坐落在筏基上，考慮到底部核島筏基板作為1個整體，對安全殼結構所起的作用按邊界條件的方式處理，在幾何模型中也沒有考慮。安全殼外殼混凝土有限元模型如圖1所示。

圖1 混凝土有限元模型Fig.1 Finite element model of concrete

1.4 撞擊荷載和分析方法

飛機對核電廠防護結構或對一般結構物撞擊問題首先要解決荷載－時間關系曲線問題［3］。確定飛機撞擊荷載函數是一個較為復雜的課題，經過大量的研究，這些載荷函數已或多或少標準化了［4］。本文撞擊荷載選用我國由國家核安全局批準發布的HAD101/04《核電廠廠址選擇的外部人為事件》［1］附錄I飛機墜毀中的波音707－320型飛機，波音707－320相對應的荷載/時間函數如圖2所示［1］，對應的撞擊面積/時間函數如圖3所示［1］，計算中選用的撞擊面積平均值，對平面約為37 m2，對球面約為18 m2。

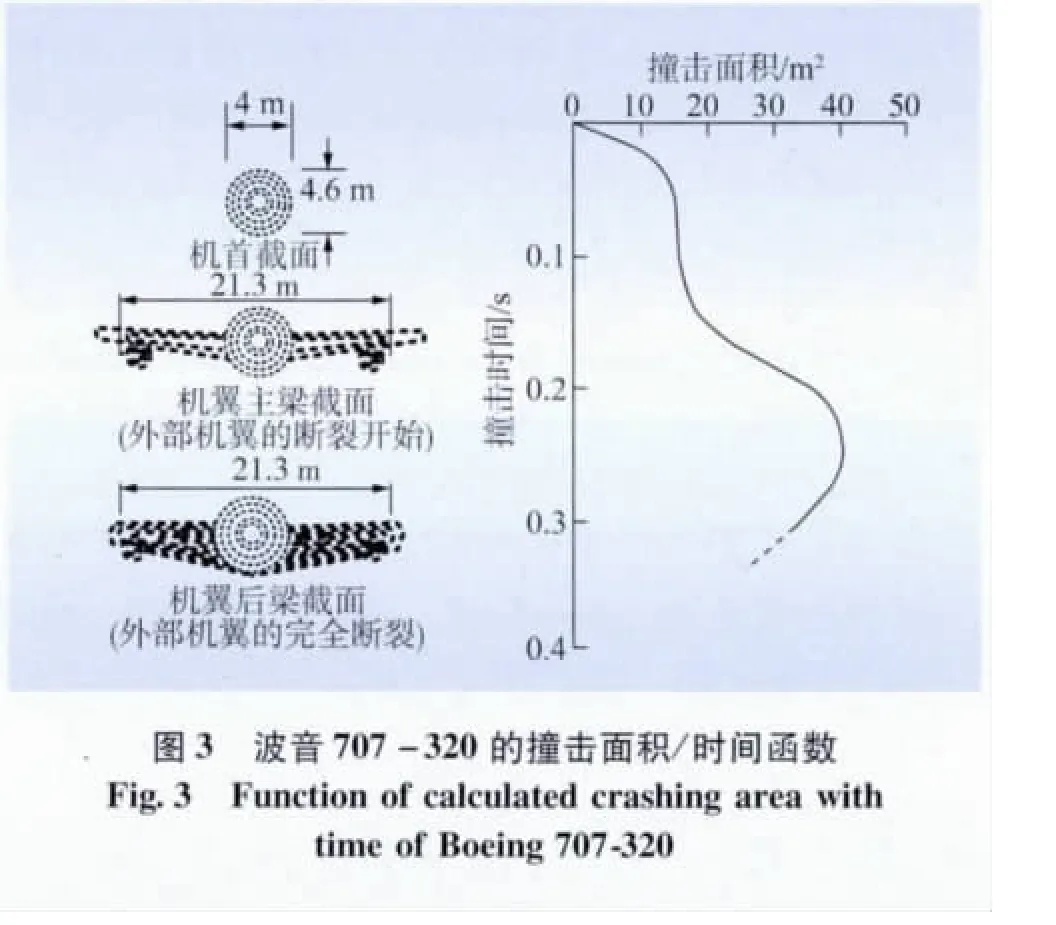
由撞擊荷載/時間函數特點可見，撞擊載荷隨著機身結構(撞擊接觸面積)變化而呈現逐漸增大趨勢，當撞擊時間達到0.15 s時，載荷值迅速增大并在0.25 s時達到峰值，可判斷0.15 s為機翼開始接觸到撞擊面的起始時刻，0.25 s時最堅硬部件引擎所造成的撞擊使得載荷力達到最大值，隨著撞擊面積的逐漸減少，載荷力也隨之減小。

本文采用在混凝土墻面直接施加撞擊載荷力的方式進行等效波音707－320型飛機撞擊分析，獲得外殼結構的撞擊響應結果。等效撞擊載荷曲線分為2段，分別作用于機身和機翼所代表的面積上。在LS-DYNA中撞擊荷載通過在相應撞擊區域內施加撞擊方向的節點力來實現。

根據飛機的特征，其撞擊作用可以分為2部分，一部分是機身部分的撞擊(等效為圓形區域)，另一部分是機翼部分的撞擊(等效為矩形區域)。安全殼撞擊位置的正視圖如圖4所示。

圖4 安全殼撞擊位置Fig.4 Front view of crashing location on containment

2 材料本構模型

分析飛機撞擊的瞬時響應，關鍵是正確描述鋼筋混凝土安全殼的材料非線性本構關系和失效準則［5］。在大應變、高應變率、高圍壓條件下，選擇合理的混凝土材料本構模型對于此類研究具有重要意義。研究人員構建了很多混凝土材料的動態本構模型，其中以經過 Johnson-Cook 模 型［6］改 進 的 Johnson-Holmguist-Concrete模型［7］應用最為廣泛，該模型能很好地描述高應變率條件下混凝土的響應問題，綜合考慮了大應變、高應變率、高壓效應，非常適合于Lagrange和Euler程序的計算［8-9］。本文采用此模型(MAT_JOHNSON_HOLMQUIST_CONCRETE)［2］(HJC) 來模擬混凝土。HJC混凝土模型包含5個強度參數A，B，N，C和SMAX(其中A表示標準化的凝聚力強度，為混凝土無損傷壓強度與完全壓碎抗壓強度之差;B，N表示壓力強化系數和壓力強化指數;C，SMAX表示應變率系數和最大標準化等效應力);7個狀態方程參數;4個損傷定義參數。該模型將材料變形分為形狀改變和體積改變。破壞面方程用來表示形狀的改變，狀態方程用來描述體積的改變，損傷也具有壓力依賴性［10］。

采用(MAT_ADD_EROSION)［2］侵蝕失效準則來控制混凝土單元的失效，該模型有壓力、等效應力、切應變、主應力、臨界應力、主應變、應力脈沖失效等7種失效方式。本文采用等效應力失效方式。混凝土的單元類型為六面體實體單元，算法為單點積分(constant stress single point integration)［2］。在模型中，鋼筋采用LS-DYNA中分段線性動力硬化本構模型(MAT_PLASTIC_KINEMATIC)［2］。鋼筋的單元類型為三節點梁單元，算法為單點高斯積分(hughesliu)［2］。在高速碰撞過程中，材料的強度隨應變率的提高而增加，而材料的彈性模量和泊松比對于應變的變化敏感性較弱，通常進行分析時可不考慮應變率的影響。對于飛機撞擊對結構產生的應變率一般為0.05～1.0 Hz，需要考慮應變率對鋼筋和混凝土強度的影響。因此，在分析中對靜力狀態下材料的強度值做適當修正是合適的。本研究采用NEI07－13報告［11］中推薦的動力強化系數來考慮此特性。混凝土抗壓強度的動力增大系數(DIF)一般取1.15，抗拉強度的動力增大系數一般取1.20，鋼筋的屈服強度的動力增大系數一般取1.10。

3 撞擊結構分析

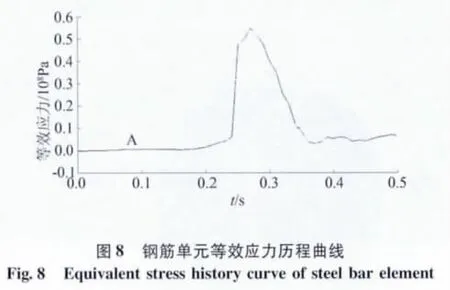
圖5為安全殼撞擊的最大位移云圖，取變形中心附近的5個節點的位移，獲得其撞擊過程的位移時間歷程曲線如圖6所示。圖7～9分別給出了安全殼撞擊的鋼筋等效應力云圖、等效應力歷程和鋼筋塑性應變云圖。

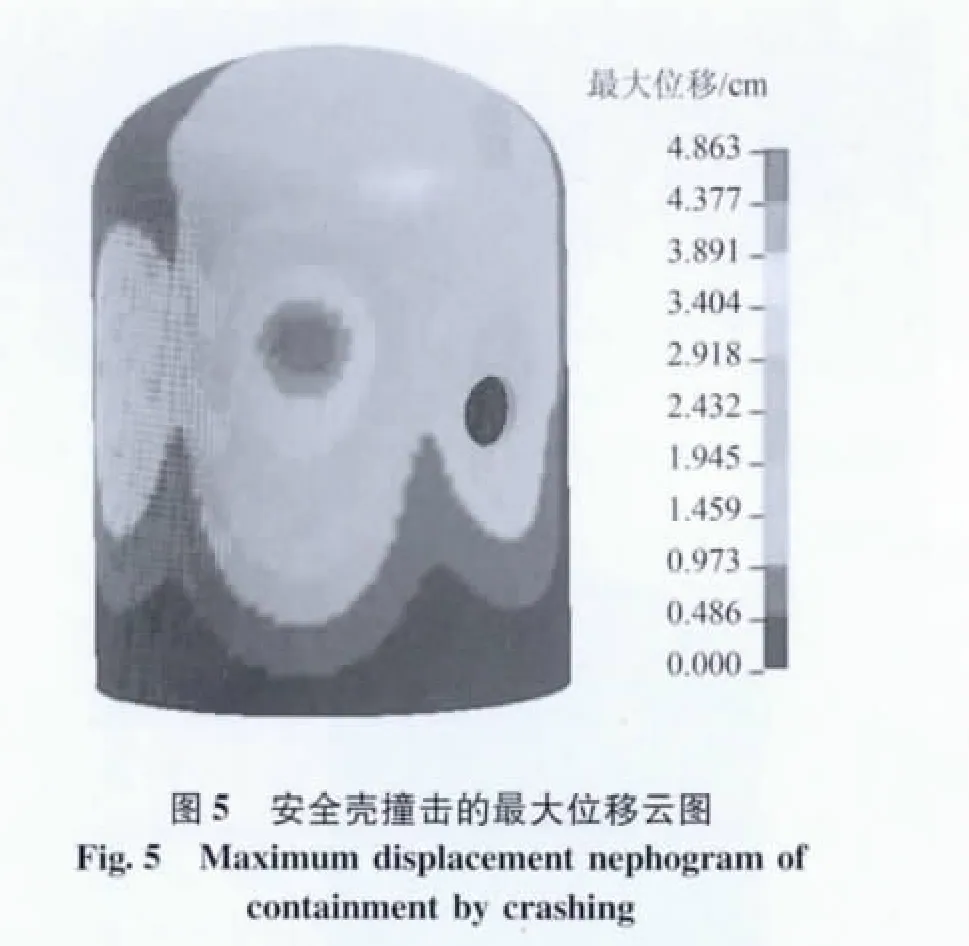
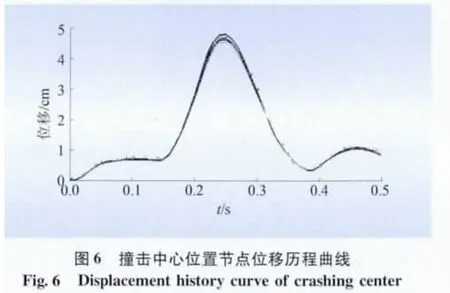
由圖 5、6可知:在撞擊荷載力的作用下，在0.25 s時刻，安全殼撞擊區域達到變形最大值，最大凹陷深度4.8 cm左右，向殼身徑向變形。撞擊造成的變形峰值約為4.8 cm，遠小于內殼和外殼之前的空隙1.5 m，因此內殼并未受到撞擊。由圖7、8可知，在撞擊的 0.27 s左右，鋼筋最大等效應力為5.5×108Pa，達到了屈服極限，進入塑性變形。由圖9可知，鋼筋的最大應變為0.0446%，遠小于鋼筋允許的最大應變5%，鋼筋沒有破壞。

4 結論

某反應堆安全殼外殼在HAD101/04中提供的波音707－320飛機撞擊作用下，安全殼內的鋼筋屈服，但是并未達到鋼筋的最大允許應變，安全殼的最大變形未超過內殼與外殼的間距。因此，能滿足NRC對抵抗飛機撞擊事件的相關審評要求，即能保證“反應堆冷卻能力，安全殼完整性以及乏燃料池的完整性和冷卻能力”不受損害。同時，無論鋼筋的應變率還是安全殼最大變形量都遠遠小于允許值，這也說明像波音707－320型這樣的小型商用飛機對核電廠安全殼的影響是很小的，但是大型商用飛機對核電廠安全殼的影響則有待進一步深入的研究。

［1］HAD101/04核電廠廠址選擇的外部人為事件［S］.北京:中國法制出版社，1989.

［2］Livermore Software Technology Corporation.LS-DYNA keyword user's manual［M］.California:Livermore Software Technology Corporation，2007:307，1394.

［3］王遠功，余愛萍.飛機撞擊核反應堆安全殼荷載－時間曲線的確定［J］.核科學與工程，1991，11(3):208-215.

［4］左家紅.秦山核電廠安全殼在飛機撞擊下的非線性分析［J］.核科學與工程，1992，12(1):35-42.

［5］李笑天，何樹延.飛機撞擊核反應堆安全殼的動力學分析［J］.核動力工程，2004，11(3):426-429.

［6］Hallquist J O.LS-DYNA Theory Manual［M］.California:Livermore Software Technology Corporation，2005:259.

［7］Holmquist T J，Johnson G R，Cook W H.A computational constitutive model for concrete subjected to large strains，high strain rates，and high pressures［C］//14th International Symposium on Ballistics，1995:591-600.

［8］溫萬治.網格線示蹤點法(MOCL)及其在數值模擬中的應用［R］.北京:北京理工大學機電工程學院，1998.

［9］馮國忠.基于ANSYS/LS-DYNA的混凝土靶板侵徹問題的數值模擬與分析［D］.哈爾濱:中國地震局工程力學研究所，2006.

［10］姜華，王君杰.彈體侵徹混凝土數值模擬失效指標研究［J］.振動與沖擊，2009，28(8):30-34.

［11］The Nuclear Energy Institute.Methodology for performing aircraft impact assessments for new plant designs［R］.Walnut Creek，California:The Nuclear Energy Institute，2009.