基于動態貝葉斯網絡的電子戰效果評估＊

付得才

（91515部隊 三亞 570216)

1 引言

電子戰戰場監控及目標毀傷評估是在上一次對電子戰目標實施攻擊后，對其毀傷情況進行查明和判定的過程，這是其作為目標選擇程序環的中繼階段，即對前一個循環的目標選擇與打擊工作做一個全面的評估，以期為分析電子戰進程，明確制電磁權等新的循環步驟提供可依據的數據［1］。當前對電子戰效果評估的研究，多是從目標的裝備性能如：雷達功率、增益、工作頻段、重復頻率等入手，突出的是裝備的效能分析。而在實際的作戰指揮上，指揮人員更關注目標的戰術效能，比如探測距離、探測范圍、預警時間等。通過計算受到干擾時目標的戰術效能與未受干擾時作比較，得到效能下降的程度，就可以判斷出電子戰是否達到預期的效果［2］。

同時，動態貝葉斯網絡不僅具有貝葉斯網絡的優點，而且考慮到了時間因素對變量的影響，具有較強的實時性，能夠實現信息在時間上的積累和互補，具有強大的濾波平滑功能。這種特點正好適合在戰場上根據各種不確定或不完整的目標毀傷信息對目標毀傷等級進行綜合評估。為此，本文將基于動態貝葉斯網絡技術對電子戰效果展開評估。

2 動態貝葉斯網絡概念

要在靜態貝葉斯網絡的基礎上建立動態貝葉斯網絡模型，首先要進行一些假設，即引入Markov假設和轉移概率時不變假設［3］。通過這兩個假設，動態貝葉斯網絡可以由兩個貝葉斯網絡構成：一個是初始化網絡B0；另一個是轉移網絡B→。B0定義的是當前過程中初始化狀態的概率分布p（x［0］)；B→定義的是對于每個時間點0，1，…，t，在t和t＋1時刻之間的狀態轉移概率p（x［t＋1］｜x［t］)［4～5］。通過利用動態貝葉斯網絡將靜態貝葉斯網絡擴展到對時間演化的過程，反映變量的發展變化規律，可以用來解釋動態的數據并對未來態勢進行分析和預測。其圖形模式如圖1所示。

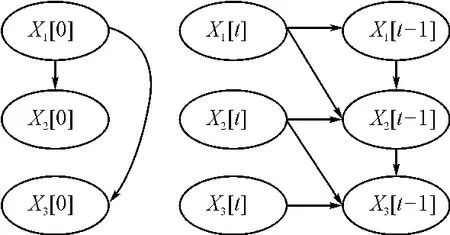
圖1 動態貝葉斯網絡結構

3 電子戰效果評估變量提取

本文將重點從航空兵作戰的需要出發，一是選擇我方在戰場上可以實際監測到的敵方目標參數為原則；二是選擇的目標參數要能反應電子戰效果為原則，對我方的有效干擾壓制進行評估［6］。

3.1 雷達觀察扇區損失度量［7］

壓制性干擾對搜索雷達進行干擾，是在雷達終端顯示畫面上出現密集亮點，即形成干擾扇面，淹沒雷達回波信號亮點，從而雷達有效觀察目標的區域減小，這減小的程度可度量干擾效果，可用下式衡量雷達觀察扇區損失程度：

式中：S0為雷達正常觀察扇區面積；SJ為干擾扇區面積。

3.2 雷達發現距離損失度量［8］

發現距離是搜索雷達設計的重要指標，當遭到干擾時，遠距離的目標由于在雷達輸出端的信噪比較小，使得雷達很難探測到，因此雷達發現目標的距離將會下降，下降的程度描述了干擾效果，可用下式衡量：

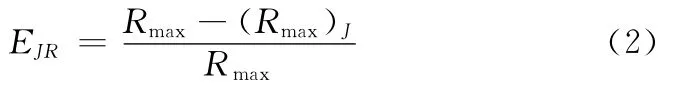
式中：Rmax是雷達正常的目標發現距離；（Rmax)J是雷達受干擾后目標的發現距離。

3.3 雷達發現概率下降度量

發現率下降度：在干擾條件下雷達的實際發現率，與雷達在正常條件下發現率的差值。干擾越強烈，下降度越大［9］。其表達式為

式中：m為在干擾條件下實際發現的目標批次數；n為進入雷達探測范圍的目標批次數；P為正常情況下雷達的發現概率，以近似于1考慮。

3.4 突防概率增加度量［10］

航空兵突防概率的變化可以定義為

式中：Ppe為未受干擾時的突防概率，且Ppe＝（1－PD1)（1－PD2)（1－PD3)，PD1為突防飛機被敵方殲擊機殺傷的概率，PD2為被敵方地空導彈殺傷的概率，PD3為被敵方火炮殺傷的概率；P′pe為干擾情況下的突防概率。因此，只要知道在有無干擾條件下敵方殲擊機、防空導彈和火炮的殺傷概率，就可以對干擾效果做出評價。

4 動態貝葉斯網絡在電子戰效果評估中的應用

4.1 電子戰效果評估模型

基于上節分析，我們可以構建一個電子戰效果評估動態貝葉斯網絡模型。如圖2所示。

圖2 電子戰效果評估動態貝葉斯網絡模型

模型中變量的狀態集合如下：

電子戰效果等級＝［不受干擾、輕、中、重］；

觀察扇區損失度＝［輕、中、重］，其中EJS＝［0，0.3］為輕，（0.3，0.6］為中，（0.6，1］為重；

發現距離損失度＝［輕、中、重］，其中EJR＝［0，0.3］為輕，（0.3，0.6］為中，（0.6，1］為重；

發現概率下降度＝［輕、中、重］，其中EJD＝［0，0.3］為輕，（0.3，0.9］為中，（0.9，1］為重；

突防概率增加度＝［低、中、高］，其中EJP＝［0，0.2］為低，（0.2，0.6］為中，（0.6，1］為高。

4.2 模型參數設定

條件概率矩陣反映的是領域專家對于網絡中關聯節點之間因果關系的看法，是一種專家知識。根據專家經驗，由觀察扇區損失度、發現距離損失度、發現概率下降度、突防概率增加度推理出電子戰效果等級，采用概率方式描述如表1所示。

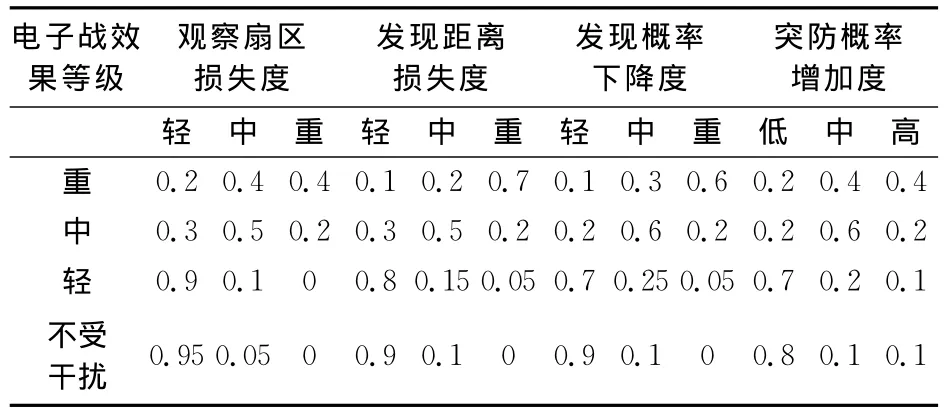
表1 電子戰效果等級條件概率表

在網絡隨時間變化的同時，兩個時間片之間的狀態轉移概率是隨機概率，如表2所示。

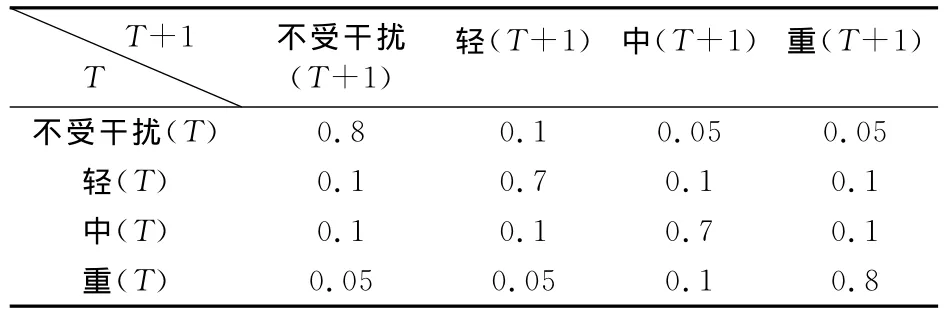
表2 動態貝葉斯網絡的狀態轉移概率表

值得指出的是，條件概率矩陣是一種專家知識，難免存在一定的主觀性，可以采用樣本數據反復調試的方法，對矩陣數據進行適度調整，以提高評估結果的可信性。

5 仿真算例

這里對基于動態貝葉斯網絡的電子戰效果評估是建立在已觀測信息基礎之上的（目標特征參數)。我們利用第3節所給出的模型和網絡參數建立用于效果評估的動態貝葉斯推理圖形，仿真平臺為netica［11］。如圖3所示。

圖3 基于動態貝葉斯網絡的電子戰效果評估等級推理圖形

這里值得指出的是由于輸入模型的目標特征參數的觀測值大部分都是模糊分類的結果。由于戰場環境信息源的不確定性，我們輸入模型的證據是以概率表達的似然證據。

假設預先沒有任何情報信息，設定某一目標電子戰效果等級初始狀態為不受干擾、輕、中、重的概率分別為0.25、0.25、0.25、0.25，這是一個合理的假設，反映了預估者由于信息匱乏導致對可能性評估不充分，認為各種情況的可能性均相近。初始化后，評估系統準備完畢，進入等待。當系統得到新的情報信息，即網絡的葉節點信息得到更新，則觸發網絡推理，更新整個網絡節點的概率分布，最終獲得根節點狀態的概率分布情況，完成對效果等級的一次評估，得到的結果為根據目標特征參量在該時間段內的變化得到的電子戰效果等級。

現在，我們假設每個觀測節點的證據已經給出，并假設它們是相互獨立的。從我方對目標進行電子進攻后，利用電子戰飛機實時對目標進行觀察，連續觀測10個時刻，根據不同時刻得到的證據，設定目標10個時刻的觀測值，如表3所示。

表3 目標觀測證據

通過上面給出的觀測證據，可以看出來，隨著我方對敵方目標電子進攻時間的增加，目標觀察扇區損失度、發現距離損失度、發現概率下降度越來越大；我方航空兵突防概率不斷增大；相應目標的電子戰效果級別也應該越來越高。把上述證據輸入到效果等級評估模型中，仿真結果如表4所示。

表4 各個時刻仿真結果

從以上仿真結果中可以看出目標的電子戰效果等級隨著打擊次數的增加，不斷增高；從時刻8開始，我方的電子戰效果等級有了明顯的提高。

另外，從容錯能力上來說，假設在第5次觀測時，出現了觀測錯誤，觀察扇區損失度為（0.2，0.3，0.5)，發現距離損失度為（0.2，0.3，0.5)，發現概率下降度為（0.2，0.3，0.5)，突防概率增加度為（0.3，0.2，0.5)；實際值應為（0.5，0.3，0.2)，（0.5，0.3，0.2)，（0.5，0.3，0.2)，（0.5，0.2，0.3)。這時動態貝葉斯網絡結合t＝5時刻前以及t＝6時刻的信息，對t＝5時刻的觀測數據進行濾波，得出的推理結果是（0.57，0.214，0.0723，0.144)，目標很可能還是處于完好狀態，如圖4所示。而靜態貝葉斯給出的推理結果是（0.0768，0.0954，0.236，0.592)，錯誤的判斷目標很可能已被重傷，如圖5所示。從此可以看出，動態貝葉斯網絡在觀測值出現大量錯誤時，仍然能給出正確的估計結果，具有強大的濾波平衡功能。

圖4 t＝5時在錯誤觀測下DBN給出的推理結果

圖5 t＝5時在錯誤觀測下BN給出的推理結果

6 結語

仿真結果表明，動態貝葉斯網絡能夠綜合目標不同的毀傷效果信息進行較為合理的評估；另外還針對動態貝葉斯網絡的準確性以及容錯能力，與靜態貝葉斯網絡進行了對比分析，結果表明動態貝葉斯網絡無論在準確性上，還是在濾波平滑能力上都要優于靜態貝葉斯網絡，給指揮員提供有利可靠的決策支持。

［1］費維琦.海軍戰役電子戰目標選擇過程探討［J］.國防科技，2008，29（06)：5760.

［2］孫冠倫.寬帶干擾信號的產生與干擾效果評估［D］.西安：西安電子科技大學，2010，01：4362.

［3］趙曉輝，等.動態貝葉斯網絡在戰場態勢估計中的應用［J］.電光與控制，2010，17（01)：4448.

［4］唐政，高曉光.基于離散動態貝葉斯網絡的輻射源目標識別研究［J］.系統仿真學報，2009，21（01)：117121.

［5］王雙成.貝葉斯網絡學習、推理與應用［M］.上海：立信會計出版社，2010，02：204214.

［6］肖秦琨，高曉光.動態貝葉斯網絡的無人機炮火校射［J］.火力與指揮控制，2006，31（11)：3841.

［7］黃高明.雷達遮蓋性干擾效果評估度量方法研究［J］.現代雷達，2005，27（08)：1013.

［8］唐吉祥，沈云山.卡爾曼濾波器在炮位偵察雷達中的應用［J］.電光與控制，2004，11（1)：4849.

［9］蘇暢，宋亞兵，王力軍，等.考慮天氣因素的飛機作戰效能對數模型［J］.電光與控制，2008，15（1)：2630.

［10］溫浩.用神經網絡方法實現復合干擾效果評估［D］.西安：西安電子科技大學，2005，01：4154.

［11］Norsys Software Corp.www.norsys.com.