改進PSO算法在圖像配準中的應用

王 鶴，謝 剛

(太原理工大學信息工程學院，山西 太原 030024)

責任編輯:時 雯

圖像配準是指對不同時間、不同場景的多幅圖像進行空間上的幾何變換，這樣就使得代表相同的結構像素在空間上達到一致性［l－2］。過去的幾年來，該技術得到了迅猛的發展。就圖像配準步驟而言，它一般包括3個步驟:首先，確定配準圖像與浮動圖像的坐標系，并且定義坐標系之間的關系;其次，定義相似性測度作為判別準則;最后，應用優化算法。其中，第2步與第3步是圖像配準的核心。圖像配準的方法一般可以分為2種:基于圖像特征和基于圖像灰度［3］。第1種方法是通過查找圖像之間共有的并且比較明顯的特征來進行參數變換。這種方法的優點是簡單并且計算效率高，然而配準的精度很大程度上要依賴于圖像特征點的正確提取［4－5］。但有時侯因為圖像比較復雜，計算機自動準確提取特征點是比較困難的，這就需要人工輔助來完成特征點的選取。然而，對于基于圖像灰度的配準方法只是利用了圖像間的灰度相似性來完成配準。由于此方法充分利用了圖像灰度信息，因此，配準準確度一般比較高。

1 標準PSO算法

Kennedy等人［4］提出了粒子群優化算法。此算法是來自于對生物群體的研究，該算法指出每一個優化問題的潛在解都可以被當做搜索空間中的一個粒子，并且每一個粒子的適應值都是由一個待優化的目標函數來決定的，每一個粒子都有自己的飛行速度，它們的運行方向和距離都是由這個速度決定的。粒子跟隨當前的最優粒子在解空間中進行搜索，在此過程中，所有的粒子會共享它們得出的最優解信息，進而利用它們的記憶來調整自己的速度和位置，不斷地進行比較，直到最終發現最優解。

假設S維空間搜索空間，其中粒子群規模為M，對于粒子群中的Xi(xi1，xi2，…，xid)則表示第i個粒子的位置，而 Vi(vi1，vi2，…，vid)表示的是第 i個粒子的速度。Pbest(bi1，bi2，…，bid)則代表的是第i個粒子目前可以搜索到的最優位置。對于整體粒子群目前為止可以搜索到的最優位置則用Pgb(Pgb1，Pgb2，…，Pgbd)進行表示。就每一代粒子而言，它的第d維速度與位置則按式(1)變化

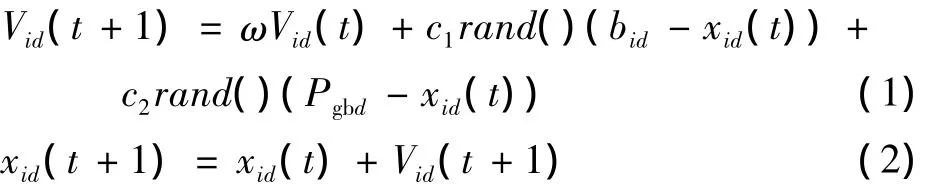
式中:1≤i≤N，1≤d≤D;c1和c2則是常數被稱為學習因子;rand()表示0～1之間的隨機數。通常c1=c2=2，ω為慣性權重系數，在本文中ω取值為0.729。并且可以根據搜索空間的維數S來求得粒子群的規模M，即

標準PSO算法的優點［5］是可以在短時間內得到高質量解。但是，它在進化過程中比較容易陷入局部最優解，使得配準精度下降。馬軍杰等［6］與張海峰等［7］曾對標準PSO進行改進。本文提出的算法在對標準PSO算法改進的同時并分別與二者相比較。

2 PSO算法改進

粒子在飛行過程中，當某粒子發現了一個當前最優解時，其他粒子便會向其靠攏。但是如果該位置是局部最優點而不是全局最優解時，就會出現所謂的“早熟”現象，為了克服這一現象，在這里提出了一個評價判斷標準——粒子相似度δ(t)

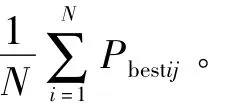
此時，式(2)不變，式(1)則為

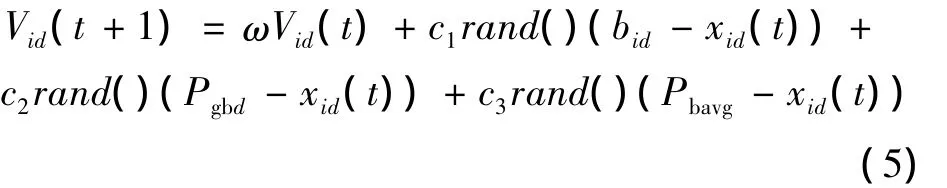
其中c3取值為2，其他參數保持不變。

對PSO進行改進后的算法流程圖如下圖1所示。

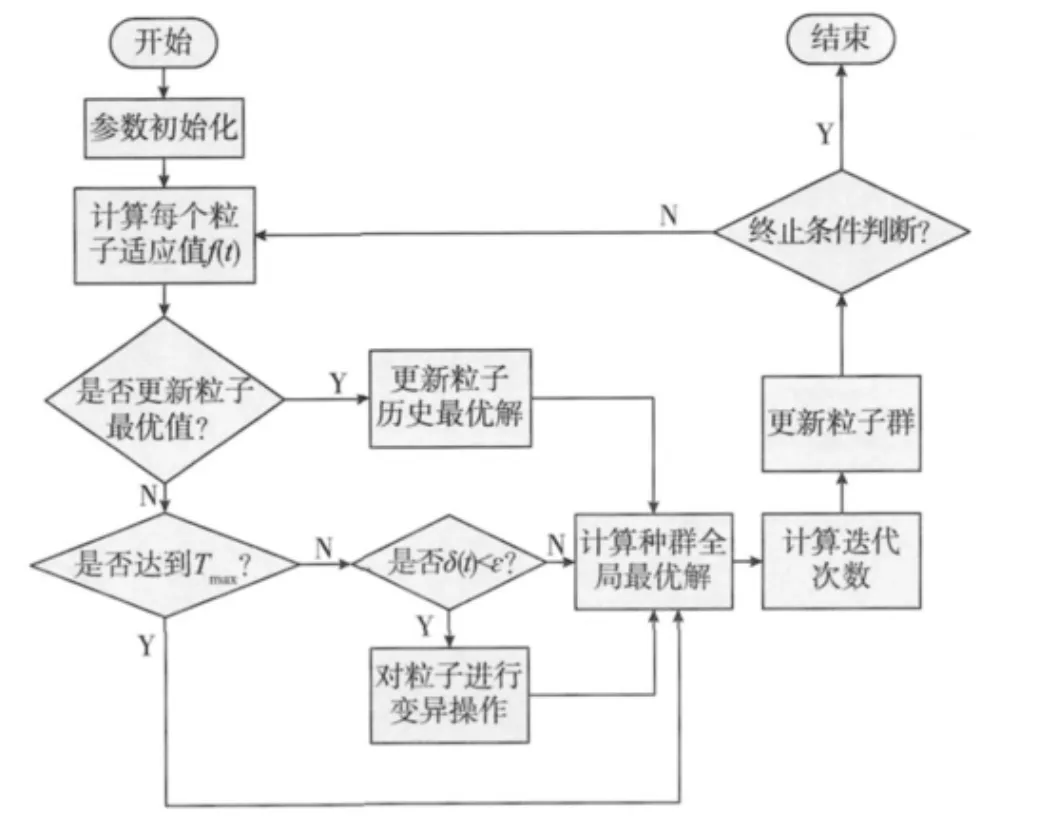
圖1 改進的PSO算法流程圖

3 圖像的相似性測度

對于配準的評價標準，稱之為相似性測度。本文選用峰值信噪比 PSNR作為相似性測度準則［8］。由于PSNR不僅可以作為用來衡量圖像灰度質量的標準，并且它可以直接從整體上反映兩幅圖像灰度上的差異.因此目前得到廣泛應用。對于相似性測度PSNR來說，當PSNR值增大時，表示的是兩幅圖像的灰度差異變小，此時圖像比較相似，圖像的恢復質量越高;反之，則表示兩幅圖像灰度差異很大并且相似度不高，恢復圖像的質量比較差。傳統PSNR定義為

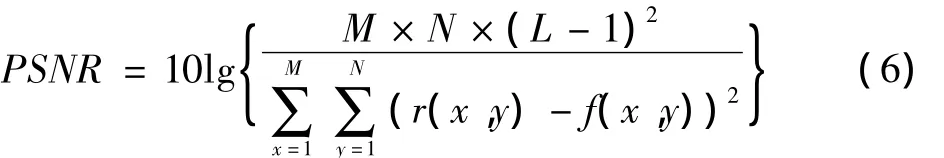
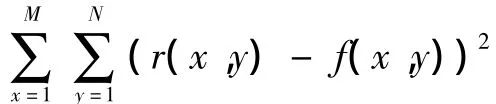
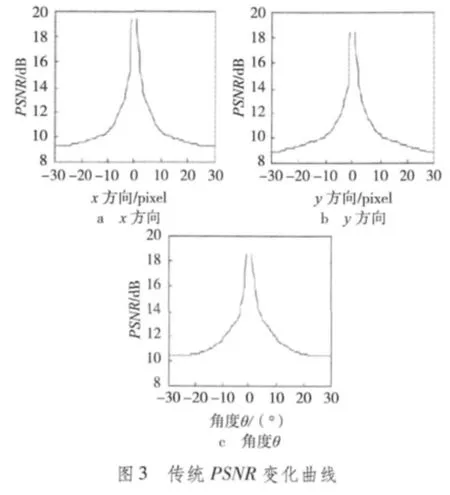
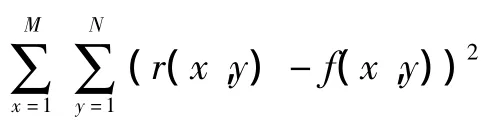
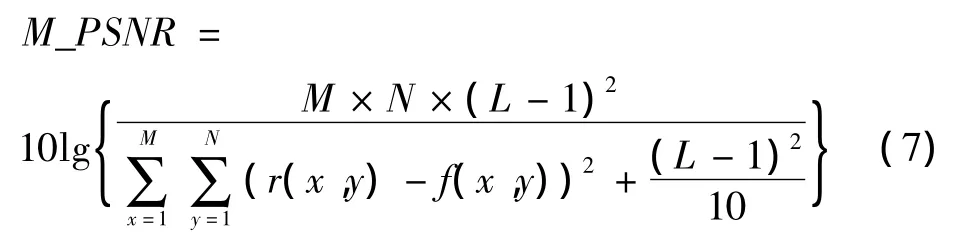
由式(7)再次對圖2進行自配準，從而得到如圖4所示的M_PSNR變化曲線。從圖4可知，M_PSNR曲線光滑連續無斷點。

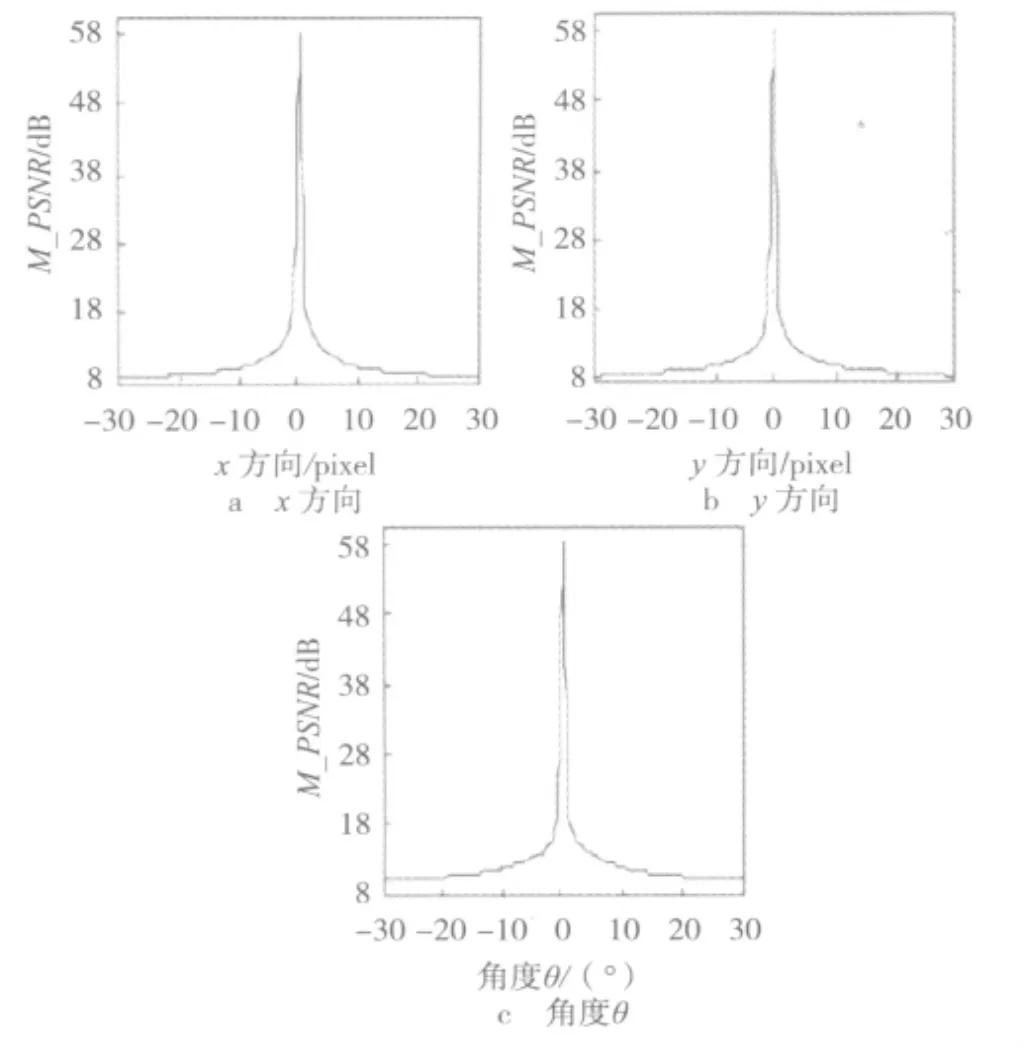
圖4 M_PSNR變化曲線

選定相似性測度M_PSNR之后，應用本文提出的算法對相似性測度在x方向、y方向和θ方向進行搜索優化。

4 模擬實驗結果分析

為了證明本文提出的算法的優良，在這里將會用文獻［6－7］所用的方法與文中方法比較。并且為了方便比較，使用η配準精度作為配準指標

式中:Δis為變換參數真實值;Δi為變換參數的實際值。

實驗中選取image－001的圖像作為參考圖像，如圖5a所示。對參考圖像做表1的變換得到image－002和image－003。

圖5 image的參考圖像和浮動圖像

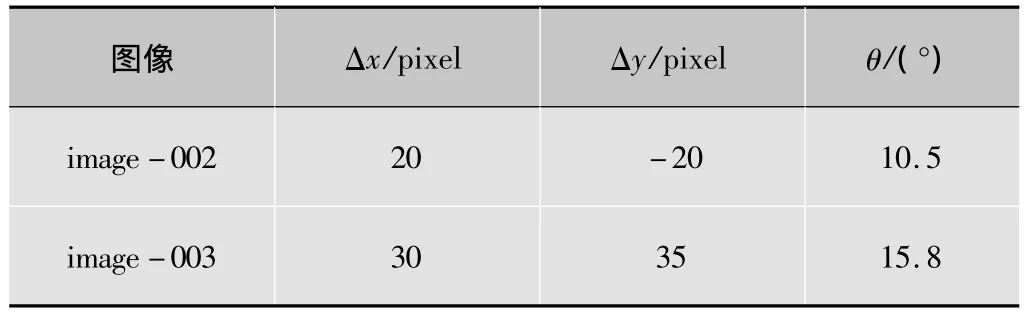
表1 浮動圖像的變換參數

實驗結果如圖6、圖7所示。

圖7 image－003實驗結果

3種方法分別對于image－002，image－003配準誤差比較如圖8、圖9所示。

圖8 image－002配準誤差比對圖

從以上圖表可知:文中提出的方法不僅在在x方向和y方向上的平移誤差均占有一定的優勢，在旋轉方面仍略勝一籌。不僅如此，從總體誤差來看，文中提出的方法精度要更高一些。因此，這是一種有效的優化算法。

圖9 image－003配準誤差對比圖

5 結論

為了解決標準PSO容易陷入局部最優解的“早熟”問題，本文提出了改進PSO優化算法。通過實驗的對比表明，文章中提出的算法配準精度高、誤差小。對于圖像配準具有很好的實際操作意義。在今后的研究工作中，可以以此展開工作來完善圖像配準精度。

［1］HAROLD S S，ROBERT W.Blind cross－spectral image registration using profiteering and ourier－based translation detection［J］.IEEE Trans.Geoscience and Remote Sensing，2002，40(5):637－650.

［2］SHANG L F，LV J C，ZHANG Y.Rigid medical image registration using PCA neural network［J］.Neurocomputing，2006，69(5):1717－1722.

［3］李磊.醫學圖像配準的研究及應用［D］.吉林:吉林大學，2011.

［4］PLUIM J，MAINTZ J，VIERGEVER M.Mutual－information－based registration of medical images［J］.IEEE Trans.Medical Imaging，2003，22(6):986－1004.

［5］李玲玲.像素級圖像融合方法研究與應用［D］.武漢:華中科技大學，2005.

［6］馬軍杰，尤建新，陳震.基于改進粒子群優化算法的灰度神經網絡模型［J］.同濟大學學報，2012，40(6):740－743.

［7］張海峰，梁工謙，張晶.基于粒子群優化模糊神經網絡的高技術知識創新評價［J］.系統工程與電子技術，2012，34(2):973－975.

［8］盤梅森，湯井田，楊曉利.采用PCA和PSNR的醫學圖像配準［J］.紅外與激光工程，2011，40(5):356－363.