RFID動態幀時隙防沖撞改進算法研究

陳春明,馮玉田，付良成

（上海大學 通信與信息工程學院，上海 200072）

射頻識別系統中，當讀寫器的讀寫范圍內有多個標簽同時存在時，這些標簽幾乎同時響應讀寫器的指令，從而產生碰撞，使得讀寫器不能正確接收標簽返回的信號。為解決產生的碰撞問題，必需采取相應的防碰撞技術。然而，由于RFID系統的特殊性，標簽無源、存儲能力有限并且不具有載波監聽能力，防碰撞算法主要考慮系統的效率、能耗等問題。目前已有一些方法來解決標簽碰撞[1]。其中比較關鍵的是如何用防碰撞算法快速和有效地將標簽全部識別出來。縱觀已有的標簽防碰撞方法，主要分為基于樹形的搜索防碰撞算法和基于ALOHA的算法[2]。樹形算法主要通過遍歷所有碰撞的節點，檢測出碰撞后讓它分成兩個分支，直到檢測到所有標簽的ID都不存在碰撞便識別完成[3]。基于ALOHA的一類算法在RFID系統中也得到了廣泛的應用。ALOHA算法類主要分為純ALOHA算法、時隙ALOHA算法和動態幀時隙ALOHA[4]。動態幀時隙最大的特點是幀的長度可根據標簽的具體情況而改變，從而保證效率的最大化。

1 動態幀時隙ALOHA的防碰撞算法分析

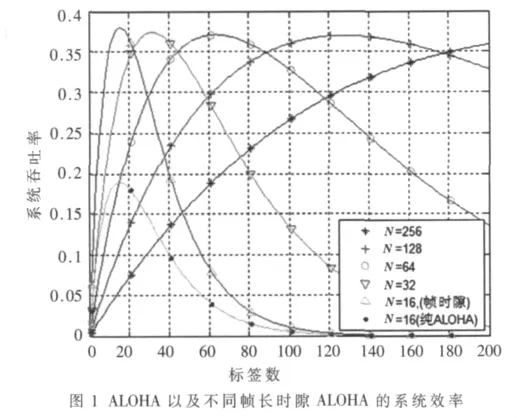
ALOHA類算法最初是從純ALOHA算法，標簽發送數據遇到碰撞則延時發送，系統效率最大能到18.4%。后來將發送時間離散化,分成若干時隙，在各時隙內發送數據也即時隙ALOHA算法，如此，因去掉了不完全碰撞，系統效率最高達到36.8%，而遇到大量標簽時效率會急劇下降。之后改進得到幀時隙算法，在時隙算法的基礎上將若干個時隙組成一幀，標簽在與讀寫器通信時隨機選擇一個時隙發送數據，幀長度由讀寫器設定，該算法的理論最大效率也是36.8%，不過可以分成若干幀來識別所有標簽。

1.1 動態幀時隙ALOHA算法

為使系統吞吐量達到最大，假設每一幀的時隙數目為M，還未讀取的標簽數為n。當一個時隙只有一個標簽的應答時，讀取標簽成功。以概率論分布統計的構造成功率的數學模型，成功時隙的統計概率為: ,

其中ps為傳輸同路的吞吐率，M為一幀的時隙數 (幀長)，n為閱讀器范圍內未識別的標簽數。固定n對M求導：

1.2 標簽估計

目前已經出現了多種標簽數目估計的方法，此類估計方法大都基于將各個時隙分為沒有標簽的空時隙，只有一個標簽的獨占時隙以及被兩個或多個標簽占用的碰撞時隙的模型設計。因為每個碰撞時隙至少有兩個或兩個以上的標簽響應，假設前一幀檢測下來有C個碰撞時隙，Lower bound method[5]則以每個碰撞時隙有最少的兩個標簽來估計，也即用N=2·C來估計閱讀范圍內未識別的標簽數量。該算法的誤差源于它只考慮了兩個標簽碰撞的有偏估計，在標簽數量比較多的情況下效率很低。FRITS C.Schoute[6]在lowerbound基礎上做了改進，考慮到每個時隙標簽大于3個的情形。通過構造泊松過程分布函數，當標簽數等于幀長的情況下得到N=2.39·C。即，用N=2.39·C來估計未識別的標簽數量，該值比lowerbound算法更為準確，但只是靜態估計不能動態反應當前幀碰撞情況。

Vogt[7]后來又提出一種不同的估計方法，根據切比雪夫不等式：一個涉及隨機變量的隨機試驗過程其輸出很可能在該變量的期望值附近。因此，可以用讀取結果與期望值之間的取得最短距離時的數值來估計標簽數目。估計模型如式(3)所示：

其中，c0、c1、ck為實際測得的成功、空閑、碰撞時隙數值。

在標簽數量 N取值范圍[c0+2ck,…,2(c1+2ck)]內找到最小的ε值，所對應的N就是估計的標簽數量。

除此之外，還有基于Bayesian理論的后驗概率估計方法[5],其系統效率有所提高但計算復雜度也變得很高。ISO-18000-6C標準中使用的Q算法[8]對系統的吞吐率作了一定的改進。但是，既然是估計算法就必然會存在估計誤差，估計算法的效果影響著系統效率。為改善估計誤差對系統效率的影響，本文提出了改進方法。

2 FBC_DFSA算法及其仿真

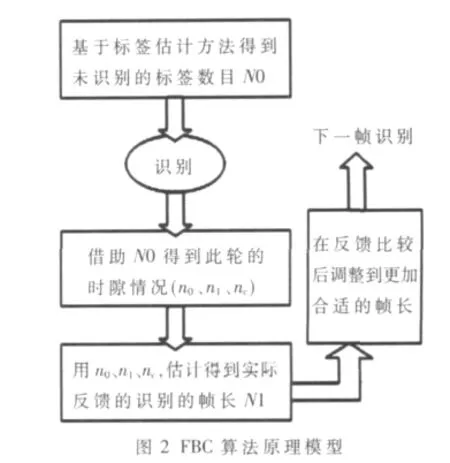
時隙幀識別法都涉及到標簽估計，但這些估計算法顯然都存在誤差。因此，本文提出FBC_DFSA算法，用估計算法得到的標簽數來設置幀長，在進行一輪識別后得到的測量結果反饋到前面估計得到的標簽數目，與其進行對比，檢驗估計算法的準確性并做出調整。本算法的原理模型如圖2所示。

首先看一下基于空閑時隙、成功時隙、碰撞時隙的一系列標簽估計，假設n個標簽在某個幀選擇了其中第i個時隙的標簽數目，概率分布為：

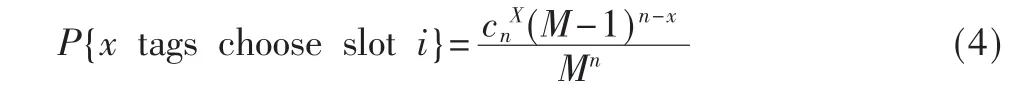
M為一幀內時隙數。如果該時隙為碰撞時隙,x≥2。得到x標簽選擇識別時隙的概率分布為:

可得到選擇時隙i標簽數目的平均值：

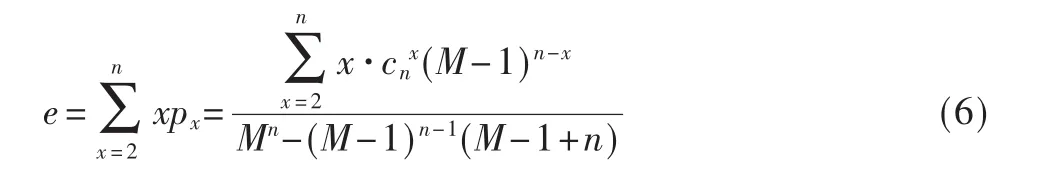
其實可以看到，當 e=2和e=2.39時，分別為 lowerbound和Schoute估計結果。Vogt方法是通過比較一個向量組中與期望值的距離來得到最佳標簽數，Bayesian算法用后驗概率分布來估計識別的標簽數目。但是，基于向量空間的搜索法 (Vogt)和基于后驗概率分布法(Bayesian)盡管在系統效率上有些改進，但是計算復雜度也比較大[9]。如圖3算法模型，基于lowerbound和Schoute的標簽估計DFSA方法來驗證FBC_DFSA算法。值也會隨之改變，雖然已經對系統效率做出了改進，但是僅僅用固定參數u對誤差進行調整還是不能更好地動態顯示當前幀情況。

因此，本文嘗試用一個隨誤差改變而自動調整的動態變量來代替u，提出了動態反饋調整動態幀時隙算法DFBC_DFSA。以下實驗選擇了用動態調整參數α|F1-F0|來代替u進行算法的仿真，其中，F1為后來計算的測量幀長，F0為之前估計的幀長，α則是調整因子。當α=1

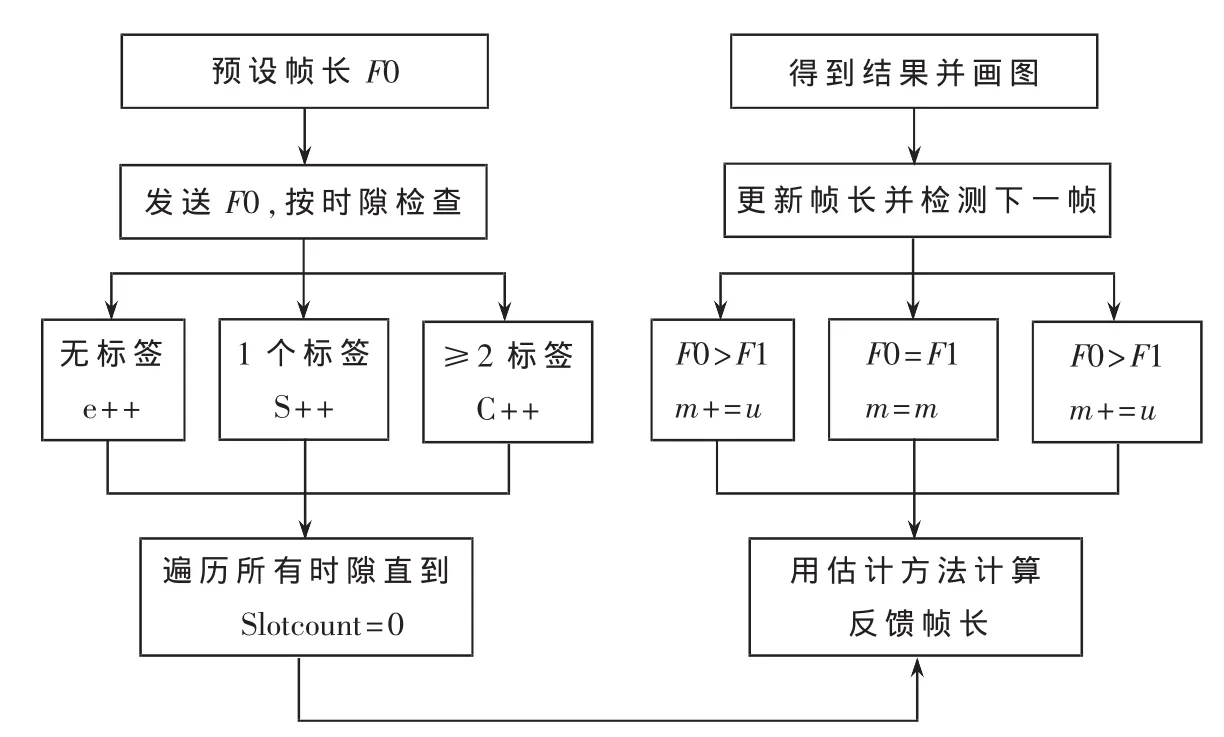
圖3 FBC_DFSA算法模型

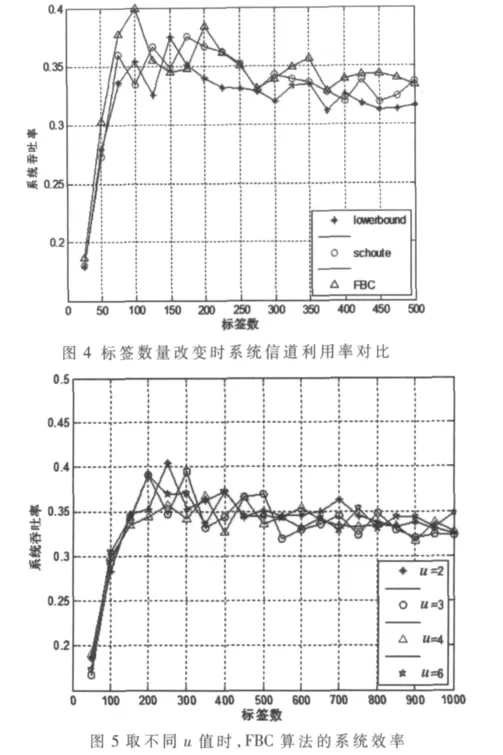
基于FBC-DFSA算法模型，再結合蒙特卡洛法的思路建立了模擬標簽識別的數學模型，并在MATLAB的環境下進行了仿真實驗，圖4給出了采用Lowerbound、Schoute以及FBC_DFSA算法時系統效率的仿真結果。

從結果可以看到，在絕大多數標簽情況下，FBC方法的系統吞吐率都要好于其他算法。

FBC_DFSA在標簽數接近幀長大小處還是能取得吞吐率的最大值，在標簽數不等于幀長的情況下，能夠對誤差做出調整，從而也可以進一步提高系統效率。但是反觀FBC_DFSA算法模型，可以看到一個比較關鍵的調整參數u，u參數決定了檢測估計結果與當前檢測結果之間的誤差調整幅度。因此，u的大小會影響整個系統的識別效率。設定初始幀長之后，在MATLAB軟件環境下進行仿真實驗，實驗部分結果如圖5所示。可以發現，在初始幀長固定的情況下，當標簽數改變時，改變參數u能夠相應地影響系統效率。

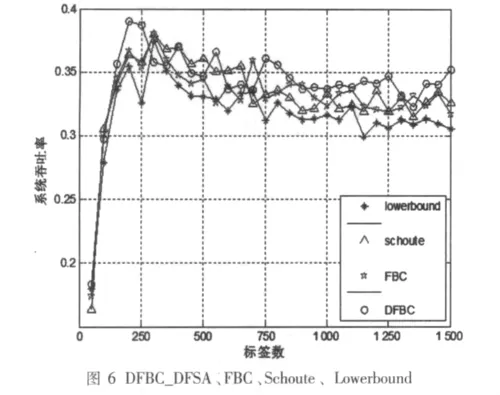
但是，隨著幀長的不斷調整，相應的估計誤差時，得到結果如圖6所示。

可以看到，此時盡管在某些標簽數量情況下，DFBC方法的效率不及固定參數u的FBC效率，但是從整體效果上看，特別是當標簽數目大于1 000后，DFBC方法的效率都有所提高，幾乎都能圍繞在0.35左右，系統的吐率表現更加穩定。

理論上講，在識別幀長與未識別的標簽數相近時，系統的效率能達到最高，但是如何得到當前閱讀范圍內的標簽數目便成了一個極為重要的問題。本文分析了一系列的標簽估計算法后，考慮到標簽估計算法的估計誤差問題,為有效地減小估計誤差并對識別幀長做出調整，提出了一種基于上述改進思路的新方法，也即FBC和DFBC動態幀時隙防碰撞算法。通過檢測后的反饋數據與之前的估計幀長作對比，可以動態地描述和調整相應的幀長。從系統效率的仿真實驗中看出，改進算法在不增加過多的計算復雜度的情況下使系統效率得到了相應的提高。而且本算法的機理可以拓展到基于其他標簽估計的動態幀時隙算法上去(像Vogt、Bayesian等)。基于FBC/DFBC的算法也能夠較為方便地應用到具體的RFID系統通信協議中去，從而在工程上真正改善RFID系統的效率。

[1]FINKENZELLER K.RFID Handbook[C].Radio-Frequency Identifications Fundamentals and Applications,2nd ed.New York:wiley,2003.

[2]MYUNG J,LEE W,SRIVASTAVA J,Adaptive binary splitting for efficient RFID tag anti-collision[J].IEEE Commun.Left,2006,10(3):144-146.

[3]Bai Chengsen,Zhu Jiang.Research on an RFID anti-collision improved algorithm based on binary search[J].International Conference on Computer Application and System Modelling(ICCASM),2010(6):430-432.

[4]程良倫，林偉勇.一種穩定高效的動態幀時隙ALOHA算法[J].計算機應用研究，2009，26(1)：85-91.

[5]FLOERKEMEIER C.Transmission control scheme for fast RFID object identification[C].IEEE International Conference on Pervasive Computing and Communications Workshops(PERCOMW),2006.

[6]SCHOUTE F C.Dynamic frame length ALOHA[J].IEEE Transactions on Communications,1983,31(4):565-568.

[7]VOGT H.Efficient object identification with passive RFID tags[C].in Proc.Int.Conf.Pervasive Computing,2002:98-113.

[8]韓振偉,宋克非.射頻識別防碰撞Q算法的分析與改進[J].計算機工程與設計，2011,32(7),2313-2318.

[9]Wu Haifeng,Zeng Yu.Tag estimate and frame length for dynamic frame slotted ALOHA anti-collision RFID system[J].Acta Automatic SINCA,2010,36(4):620-624.