基于一種組合方法的地下電纜載流量的計算及恢復

邢雅 李洪杰

（西安交通大學電氣工程學院，西安 710049）

為了使地下電纜可靠地運行和高效的傳輸，目前主要采用兩種方法來計算電纜的載流量。一種是基于國際電工委員會IEC 60287標準的熱路分析法[1-3]。另外一種是數值計算方法，常用的數值計算方法有邊界元法、有限差分法、有限容積法及有限元法[4-7]。在這些方法中有限元法能夠方便的應對各種復雜的電纜敷設環境和邊界條件，應用該方法能夠更為有效和精確的計算電纜的載流量及熱狀態。

由于土壤熱參數和周圍環境溫度是隨著季節和地形變化的，從而使得電纜的載流量在較大的范圍內變化。現代分布式光纖溫度測量系統（DTS）的發展為實時測量地下電纜表面溫度從而監測電纜的熱狀態提供了新的機會[8]。作為國家的電力公司，新加坡電力公司管理著整個新加坡的地下輸電和配電線纜網絡，其中最新的230kV電纜線路已經全部安裝了DTS[9]。

本文基于DTS測量的電纜表面溫度曲線，利用一種有限元數值計算方法與基于梯度的優化方法的組合方法估算出電纜周圍土壤的熱參數從而實現地下電纜載流量的實時評估。以實際應用的一條230kV/500MVA電纜線路為例，利用所提出的方法對其長期運行額定載流量及緊急過負荷載流量進行了精確的評估。最后，為了緩和電纜沿線的熱點從而使得整個電纜線路的載流量能夠得到較為顯著地恢復，本文采用一種通過移除電纜沿線熱點頂部填土的方法，利用大型通用有限元仿真軟件進行三維仿真分析來證明其有效性。

1 土壤熱參數的估算方法

1.1 估算方法

圖1為兩條不同傳輸容量的230kV電纜線路平面排列的敷設橫截面圖。一根DTS光纖被安裝在500MVA線路中間相表面的E點，用來測量其表面溫度。由圖1可知，一旦電纜的結構、敷設環境和負載電流確定，那么電纜的溫度分布只取決于周圍土壤的熱參數及土壤溫度。也就是電纜表面E點的溫度TE是土壤熱阻率ρsoil、熱擴散率δsoil、土壤溫度Tsoil和時間t的函數。

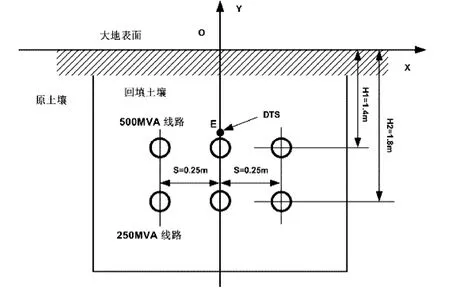
圖1 兩條230kV電纜線路的敷設截面圖

基于DTS測量溫度曲線，電纜沿線熱點可以很容易的被識別和定位。例如，圖2為230kV/500MV·A線路電纜表面溫度曲線以及最高溫度點“A”。基于最高溫度點處的電纜結構和安裝信息，這些未知的參數x=(x1, x2,…, xn)=(ρsoil,δsoil,Tsoil)可以通過最小化如下的目標函數而被估算出來

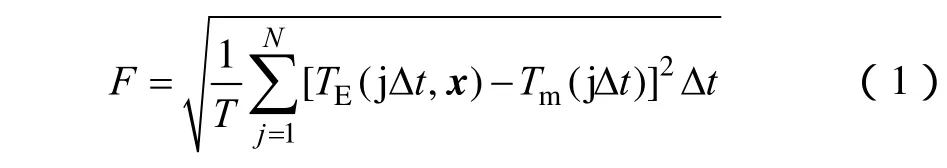
式中，N為離散測量點的總數；T是溫度測量的持續時間；Δt為測量的時間間隔；Tm(jΔt)為 E點的測量溫度（圖2）；TE(jΔt)為計算的E點的溫度，該值需要利用有限元法和優化法的組合方法來得到。

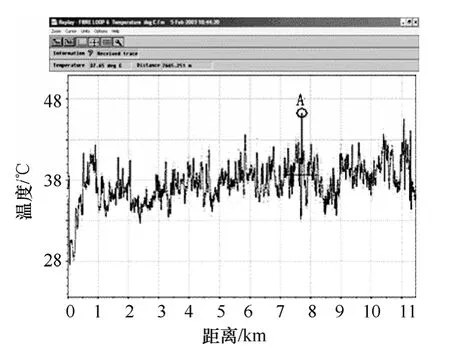
圖2 230kV/500MVA電纜線路表面溫度曲線

估算過程中，整個計算場域土壤的熱參數被看成均勻各向同性的。有了這個假設，那么土壤熱阻率和熱擴散率可以通過以下的經驗公式聯系起來[10]，即

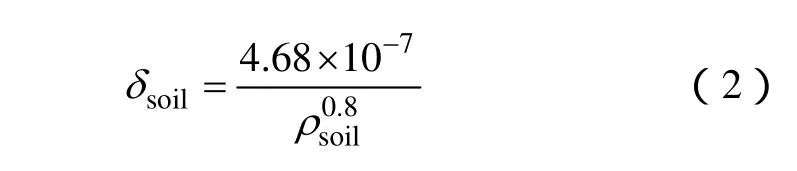
利用式（2），未知參數減少為兩個，也就是x=(ρsoil,Tsoil)，使得評估電纜熱狀態的過程更加簡單。

1.2 優化算法

本文使用變尺度法（DFP算法）來最小化目標函數（1）[11]，每一個迭代步驟k的搜索方向可以寫為

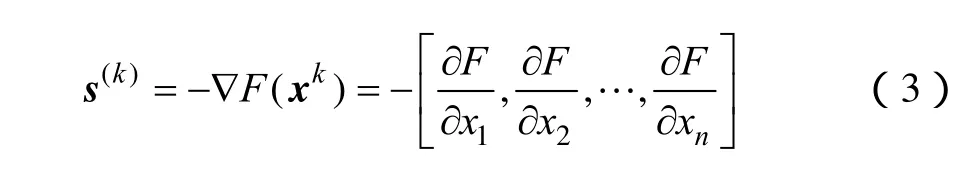
式中，xk為第k次迭代的參數向量。

式（3）中，目標函數F對第j個未知參數xj的偏導數可以寫成

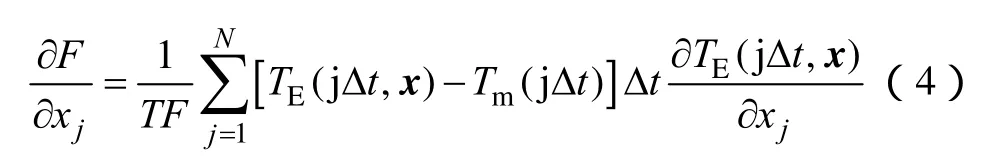
式（2）中的TE(t, x)沒有關于未知參數xj的解析表達式。因此，式（4）中的微分項可以用其中心差分形式來表示，即

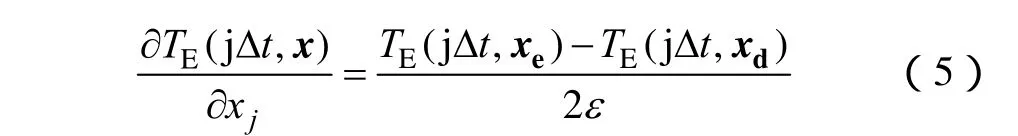
式中，ε為一個很小的擾動；xe=(x1, x2,…,xj+ε,...,xn)，xd=(x1, x2,…,xj-ε,…,xn)。

式（5）中，TE(jΔt,xe)和TE(jΔt,xd)可以使用有限元方法數值計算。

當滿足以下兩個條件后，優化過程終止。

（1）兩次連續的迭代k-1和k中第j個未知參數xj的相對變化不大于10%。

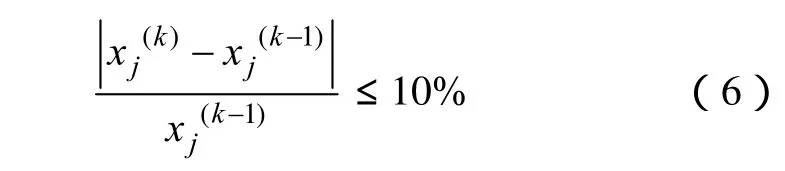
（2）目標函數F的值不超過0.5℃。

2 電纜的溫度場模型

圖1所示的電纜敷設截面圖可以簡化為一個二維溫度場，基本導熱微分方程如下[12]

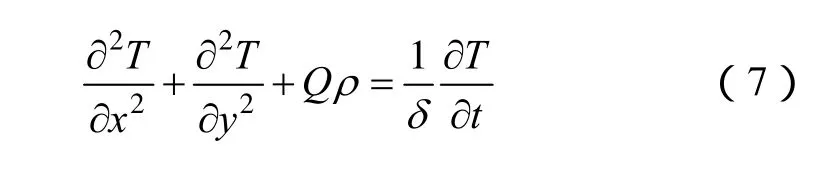
式中，x, y為空間坐標，單位為m；T為溫度，單位為K；ρ為相應材料的熱阻率，單位為K·m/W；δ為相應材料的熱擴散率，單位為m2/s；t為時間，單位為s；Q為相應區域的產熱率，包括電纜導體，絕緣層和護套，單位為W/m3，各部分的損耗可以通過IEC 60287標準給出的經驗公式計算出。

圖3所示為待研究的電纜熱場域，選擇以坐標原點“O”為中心，半徑R=10m的半圓形為計算場域，為了簡化計算，在半圓邊界Γ上，邊界條件為

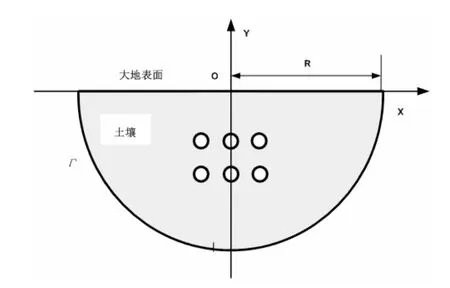
圖3 230kV電纜線路簡化熱場域

3 實例應用

本節介紹了一個典型的實例分析。所提出的研究方法被應用到評估一條安裝有DTS的230kV/500MVA電纜線路的載流量，其安裝截面圖如圖1所示。表1列出了230kV電纜的基本結構數據。

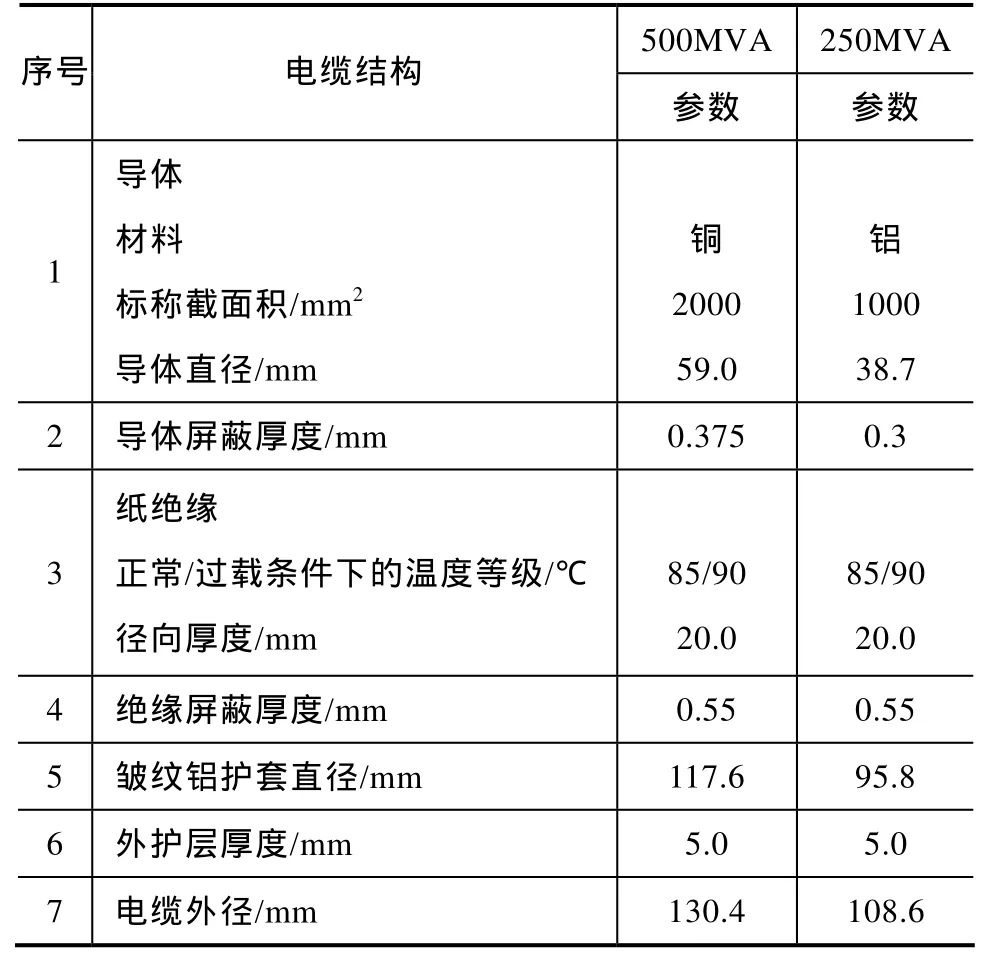
表1 兩條230kV充油電纜的基本結構參數

地下電纜沿線由于敷設環境的變化會存在很多熱點。然而，在所有的熱點中，某些位置上的熱點溫度比其他所有熱點的溫度都要高，這個最高溫度點決定了整個電纜線路的載流量。圖2中點“A”為500MVA線路中溫度最高點，因此，本文選擇熱點“A”處來評估 230kV/500MVA線路的載流量。圖4為230kV電纜線路中“A”點的現場條件圖，通過調查發現，熱點“A”形成的主要原因有三個。首先，如圖4所示，該位置在公路立交橋下方，使得雨水不能夠浸潤土壤，從而導致現場土壤非常的干燥；其次，該線路下方還存在另外一條250MVA的電纜線路，阻礙了500MVA線路的熱量擴散。最后，如圖1所示，電纜的軸向距離較近，只有0.25m，而制造商推薦的空間距離為0.3m。圖5為使用Matlab離散后的場域。由于計算場域關于Y軸對稱，因此只有一半的區域被剖分。

圖4 熱點“A”的現場環境圖

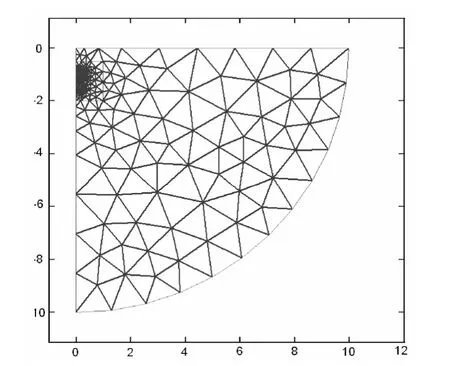
圖5 離散場域

3.1 土壤熱參數的估算

圖6所示為5天內記錄的兩條線路的負荷電流曲線、DTS所測量“A”處500MVA中間相電纜的表面溫度曲線和計算溫度。前三天的時間段里，利用測量的電纜表面溫度數據和所提出的組合研究方法來最小化目標函數式（2），從而估算得到土壤的熱參數為

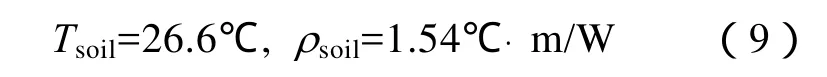
利用估算的土壤熱參數，電纜導體和表面的溫度都可以被預測。圖6中后兩天計算的溫度曲線均為預測的溫度，可以看出，從第4天到第5天預測的表面溫度與使用DTS測量的表面溫度很好的吻合。

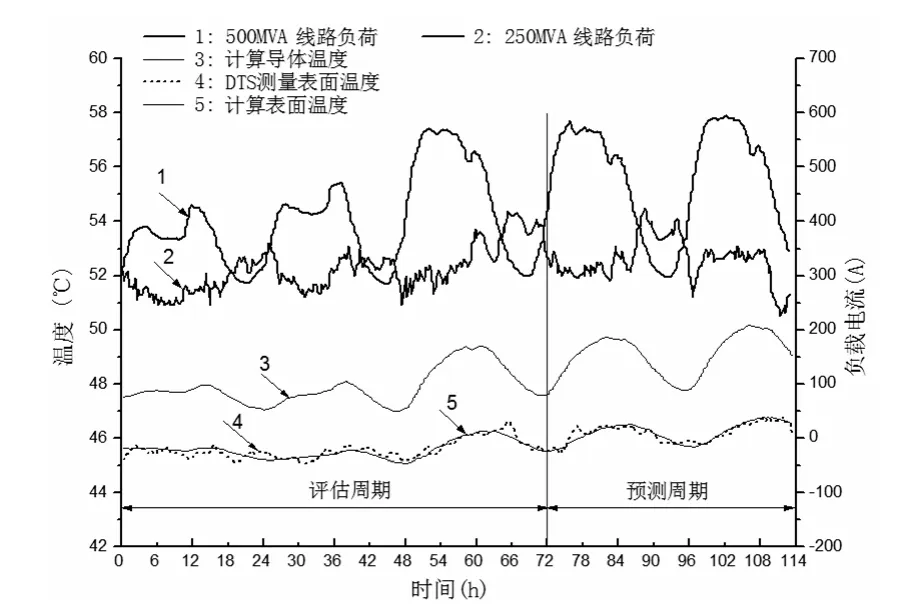
圖6 5天內兩條230kV電纜線路的負載電流、測量溫度以及計算溫度

3.2 載流量的評估

利用式（9）中估算的土壤熱參數，電纜在正常連續負荷和過負荷條件下的最大允許運行電流關于時間的曲線可以很容易的被預測。

1）持續運行載流量

持續運行載流量表示在電纜導體溫度不超過允許溫度85℃時，電纜運行時的最大恒定負載電流。利用式（9）中估算的土壤熱參數，假設250MVA線路承載了200A的負載電流，計算可得500MVA線路的持續運行載流量約為1030A，該值為標稱額定電流值1255A的82%。可以看出，500MVA線路的降額運行是必需的，降額的大小取決于250MVA線路的實際負載電流。

2）緊急過負荷載流量

緊急過負荷載流量是指電纜在特定的持續時間內能運行的最大過載電流，此時電纜導體溫度不超過容許值90℃，緊急過負荷載流量值取決于已加載電流的時間和線路可能承受過載的持續時間。圖7所示為在72h末，500MVA線路突然承受1506A電流，相當于120%標稱額定電流，與此同時，250MVA線路的負載電流為恒定的320A。從圖中可知在過載運行45.5h之后，電纜導體溫度達到90℃。進一步計算，當72h末過負荷分別為150%和180%時，持續運行時間分別為11.7h和4.7h。

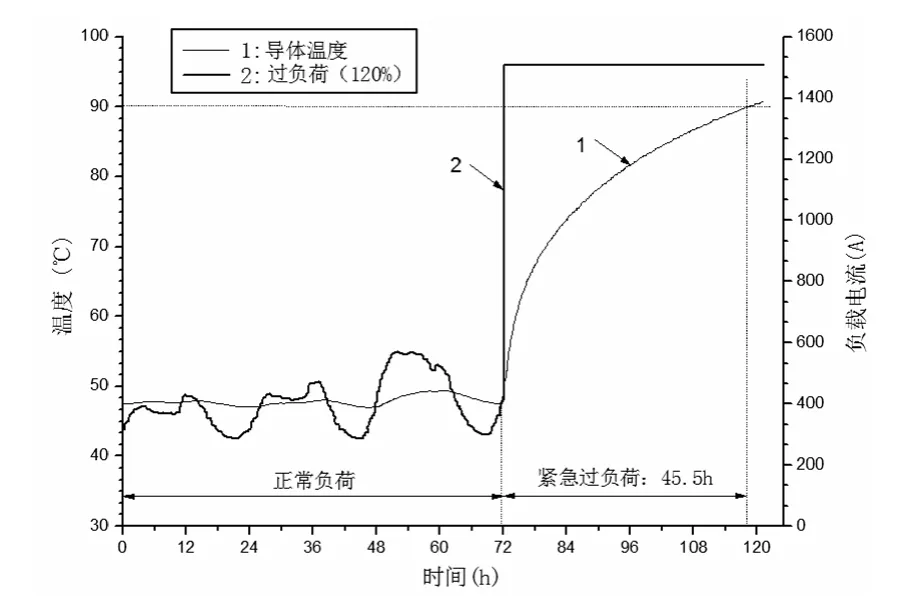
圖7 500MVA線路在120%過負荷條件下的計算導體溫度

4 載流量的恢復

在特定的現場環境下，通過調查電纜的空間距離、埋設深度、地形以及土壤熱阻率等因素，總結出形成熱點的主要因素如下。

1）電纜交叉。

2）3根或更多電纜平行敷設。

3）電纜敷設在公路立交橋下方，使得雨水不能夠浸潤土壤。

4）電纜敷設在混凝土路面下方。

5）電纜被包裹在金屬密閉空間結構中。

6）地下電纜埋設較深。

7）電纜軸向空間距離不充分。

為恢復整條電纜線路的載流量，本文采用一種通過移除電纜沿線熱點頂部填土的方法，利用有限元軟件“ANSYS”對該方法進行三維仿真分析。

為了簡化仿真過程，假設只有一條230kV/500MVA的電纜線路埋在地下，所要緩和的熱點位于坐標中心“O”。電纜及其周圍土壤的穩態溫度分布可以通過建立三維熱模型求得。由于計算場域關于YZ平面對稱，因此只建立一半區域的模型。

為了計算電纜的穩態溫度分布，仿真時需對計算場域施加3種邊界條件。

深層土壤溫度恒定，三維模型的底面為第一類邊界條件

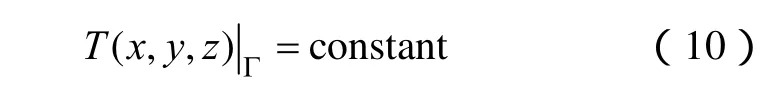
三維模型的側面水平溫度梯度為0，因此，待研究場域側面法方向的熱流密度q可以寫成

模型的頂部，也就是鄰近空氣的表面，這些面的法方向的熱流密度q可以寫成

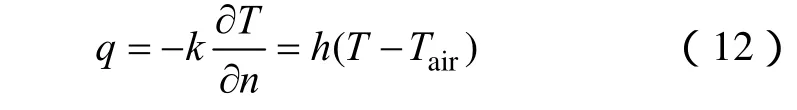
式中，h為對流換熱系數，單位為 W/m2/K；Tair為空氣溫度，單位為K。

第一類和第二類邊界條件的選擇對于溫度分布有較大的影響，改變邊界到中心“O”點的距離，當距離大于10m以后，再次曾加邊界的距離對穩態溫度分布影響非常小。因此，建立寬度為10m，高度為10m+H的半立方體模型，另外，模型在Z方向的長度取 20m，使得沿 Z軸距離熱點“O”較遠的地方溫度能夠達到穩定。通過從已建立的半立方體模型中心“O”正上方減去一個深1.2m，寬1m，長度為3m的半立方體區域來模擬本文所提出的緩和方法。電纜的結構參數和敷設參數分別見表1和表2。

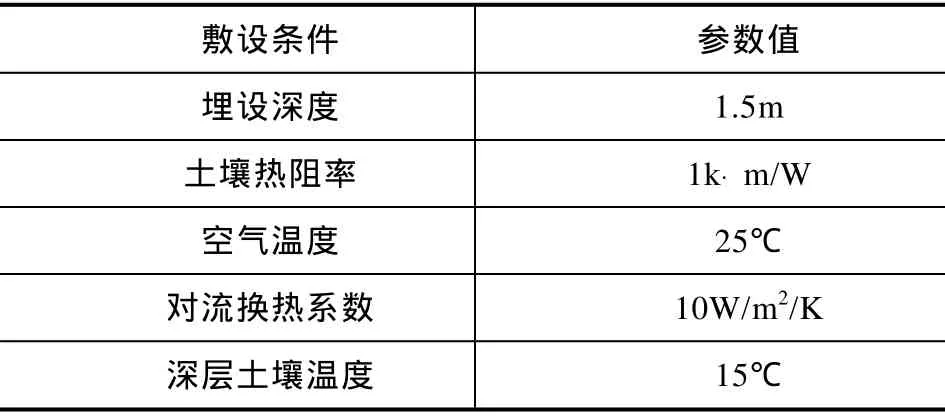
表2 230kV充油電纜的敷設參數

假設電纜承載了1255A的標稱額定電流，利用計算得到的相關區域的損耗值以及敷設參數值，電纜及其周圍區域的穩態溫度場如圖8所示。

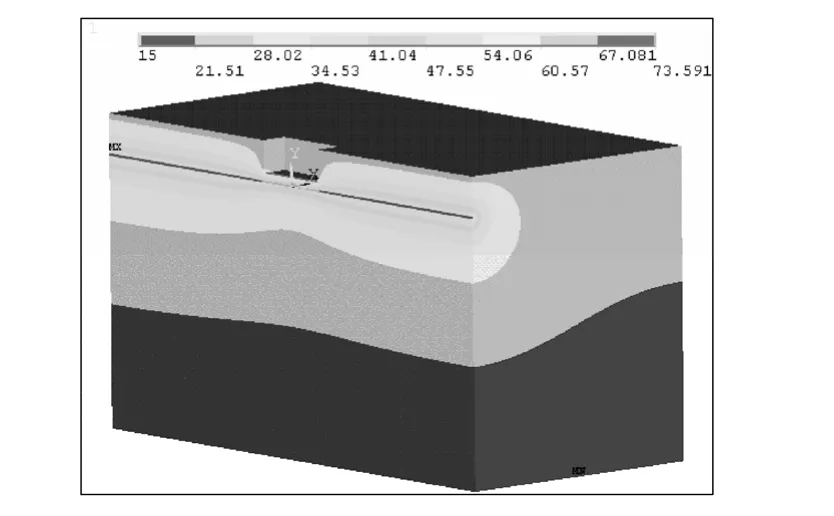
圖8 穩態溫度分布圖

圖9為沿Z軸從-10m到10m導體的溫度曲線。可以看出，隨著到中心點“O”（熱點）距離的增加，電纜導體的溫度逐漸增加，最后保持穩定在73.6℃。與距離較遠處的溫度相比較，處于中心位置“O”點的熱點溫度減小到 64.7℃。這個顯著地溫度下降證明了本文所提出的方法能有效的緩和熱點的影響，從而恢復整條電纜線路的載流量。本文的研究是從熱點“O”的上方移除一個深1.2m，寬2m，長3m的立方體區域，顯而易見的，熱點的溫度降以及電纜載流量恢復的程度和所移除的土壤區域的體積有關。移除較多的土壤有助于加強熱點上方的對流換熱過程，在實施過程中，移除土壤區域的大小取決于現場條件。

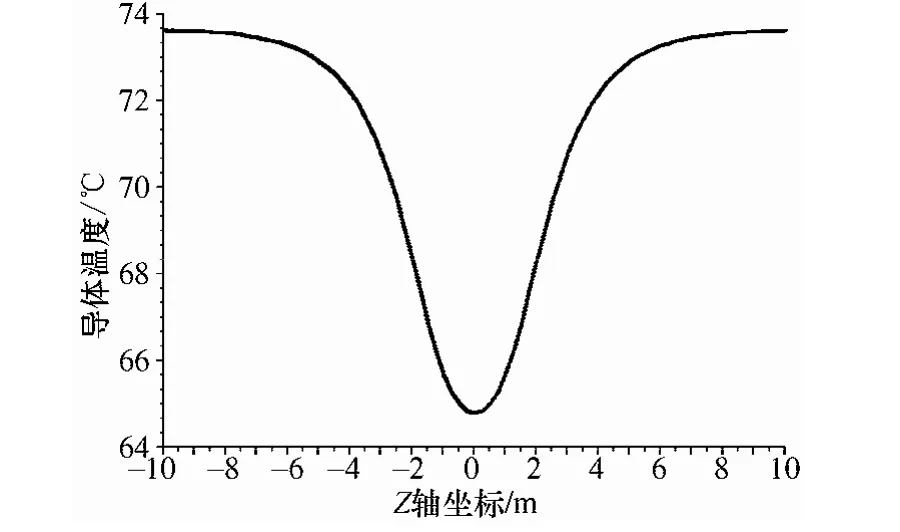
圖9 沿Z軸從-10m到10m導體的溫度曲線

5 結論

本文提出一種有限元數值計算方法與基于梯度的優化方法的組合方法，基于DTS測量的電纜表面溫度曲線，識別和定位電纜沿線的溫度最高點，并且利用該方法估算出土壤的熱參數進而實現電纜載流量的實時評估。以實際應用的一條230kV/500MVA電纜線路為例，對其長期運行額定載流量及緊急過負荷載流量進行了精確的評估，證明了該方法的正確性和有效性。

為了緩和熱點溫度并且恢復整條線路的載流量，本文采用一種通過移除電纜沿線熱點頂部填土的方法，利用大型通用有限元仿真軟件對這種方法進行三維仿真分析，結果表明熱點有顯著的溫度下降，能夠有效地恢復電纜的載流量。

[1] IEC 60287-1, Calculation of the Current Rating-Part 1:Current Rating Equations(100%Load Factor)and Calculation of Losses[S]. 2001.

[2]IEC 60287-2, Calculation of the Current Rating-Part 2:Thermal Resistance[S]. 2001.

[3]IEC 60287-3, Calculation of the Current Rating-Part 3:Sections on Operating Conditions[S]. 1999.

[4]曹惠玲,王增強,李雯靖,等.坐標組合法對直埋電纜與土壤界面溫度場的數值計算[J].電工技術學報,2003, 18(3): 59-63.

[5]王有元,陳仁剛,陳偉根,等.基于有限元法的XLPE電纜載流量計算及其影響因素分析[J].重慶大學學報, 2010, 33(5): 72-77.

[6]孟凡鳳,張兵,方曉明,等.影響直埋電纜載流量的因素的研究[J].絕緣材料, 2007, 40(3): 64-66.

[7]鄭雁翎,許志亮,張冠軍,等.采用Matlab仿真的變電站高壓進線溫度場和載流量數值計算[J].高電壓技術, 2012, 38(3): 566-572.

[8]李偉,曾宏,楊琳,等.單芯電纜實時載流量計算方法研究[J].四川電力技術, 2011, 34(4): 61-64.

[9]YOON K T, TEO D S A. Controlling and monitoring Singapore's underground grid[J].IEEE Computer Applications in Power, 1999, 12(4): 23-29.

[10] NEHER J H. The transient temperature rise of buried cable systems[J].IEEE Transactions on Power Apparatus and Systems, 1964, 83(2): 102-114.

[11]凌永祥,陳明逵.計算方法教程[M].西安:西安交通大學出版社, 2005.

[12]孔祥謙.有限單元法在傳熱學中的應用[M].北京:科學出版社, 1998.