基于曲線擬合的SINS/GPS緊密組合導(dǎo)航系統(tǒng)
肖業(yè)偉,唐辛冰
(湘潭大學(xué) 信息工程學(xué)院,湖南 湘潭 411105)
慣性導(dǎo)航系統(tǒng)具有自主性和實(shí)時(shí)性好,導(dǎo)航參數(shù)全等優(yōu)點(diǎn),但導(dǎo)航定位誤差隨時(shí)間增長,難以長期獨(dú)立工作;GPS導(dǎo)航定位具有高精度,但其抗干擾能力差,信號(hào)受可見星的限制。SINS/GPS組合導(dǎo)航,克服了各自缺點(diǎn),優(yōu)勢互補(bǔ),成為當(dāng)前各類飛機(jī)普遍采用的主要導(dǎo)航設(shè)備[1]。根據(jù)慣性導(dǎo)航系統(tǒng)和GPS系統(tǒng)的組合深度,可分為松散組合、緊密組合兩類。松散組合通常指位置、速度組合,即將慣導(dǎo)與GPS接收機(jī)輸出的位置、速度之差作為量測值,經(jīng)過卡爾曼濾波,對(duì)慣導(dǎo)系統(tǒng)的誤差進(jìn)行估計(jì)和校正。而緊密組合的基本模式是偽距、偽距率組合,以及在偽距、偽距率組合基礎(chǔ)上用慣導(dǎo)位置和速度對(duì)GPS接收機(jī)跟蹤環(huán)路進(jìn)行輔助。
SINS/GPS緊密組合導(dǎo)航在進(jìn)行信息融合時(shí),GPS鐘差會(huì)造成量測信息值的突變,這種突變?nèi)绮惶幚頃?huì)造成濾波器的發(fā)散,且量測數(shù)據(jù)的時(shí)間同步問題也是該系統(tǒng)需要解決的關(guān)鍵問題之一。基于以上分析可知,組合導(dǎo)航卡爾曼濾波器的量測信息都存在一定的滯后延遲,特別是在高動(dòng)態(tài)環(huán)境下導(dǎo)航系統(tǒng)的輸出滯后將給量測值帶來很大的誤差,若直接采用這樣的量測數(shù)據(jù)進(jìn)行卡爾曼濾波計(jì)算必然給導(dǎo)航結(jié)果帶來很大的誤差。文獻(xiàn)[2]對(duì)緊密組合的SINS/GPS復(fù)合導(dǎo)航系統(tǒng)在高速、高機(jī)動(dòng)彈道導(dǎo)彈上的可行性進(jìn)行了分析研究,實(shí)現(xiàn)了基于偽1距、偽距率的SINS/GPS緊密組合導(dǎo)航系統(tǒng)的仿真,但未考慮GPS接收機(jī)的時(shí)間同步問題。文獻(xiàn)[3]提出了一種利用GPS接收機(jī)中1PPS(Pulse Per Second)信號(hào)作為同步標(biāo)簽的時(shí)間同步方法,將IMU中的數(shù)據(jù)加上精確的時(shí)間標(biāo)簽,從而達(dá)到時(shí)間同步的目的,但是在松散組合的前提下進(jìn)行的濾波。對(duì)于量測滯后問題,文獻(xiàn)[4-5]提出將滯后量測值與其對(duì)應(yīng)過去時(shí)刻的慣導(dǎo)輸出值進(jìn)行組合導(dǎo)航卡爾曼濾波,然后再根據(jù)慣導(dǎo)其他時(shí)刻的輸出值將濾波結(jié)果遞推到當(dāng)前時(shí)刻。然而,這種方法導(dǎo)致在一次濾波計(jì)算中需要進(jìn)行一次量測更新和多次時(shí)間更新,因此算法比較復(fù)雜,而且精度也不高,很難適應(yīng)高動(dòng)態(tài)環(huán)境和高精度要求。針對(duì)此,文中提出了基于曲線擬合的SINS/GPS緊密組合導(dǎo)航系統(tǒng),分析研究了設(shè)計(jì)該系統(tǒng)時(shí)遇到的問題,進(jìn)而通過曲線擬合的方法來解決導(dǎo)航系統(tǒng)量測滯后的問題,最后對(duì)改進(jìn)后的系統(tǒng)進(jìn)行了仿真驗(yàn)證,結(jié)果達(dá)到了所要求的精度,驗(yàn)證了該方法的有效性。
1 SINS/GPS緊密組合導(dǎo)航的原理
緊密組合是組合程度較深的組合方式,其主要特點(diǎn)是GPS接收機(jī)和慣導(dǎo)系統(tǒng)相互輔助。為了更好地實(shí)現(xiàn)相互輔助的作用,通常是把GPS和慣導(dǎo)系統(tǒng)按組合的要求進(jìn)行一體化設(shè)計(jì)。緊密組合的基本模式是偽距、偽距率的組合,以及在偽距、偽距率組合基礎(chǔ)上再加上用慣導(dǎo)位置和速度對(duì)GPS接收機(jī)跟蹤環(huán)進(jìn)行輔助,也可以再增加對(duì)GPS接收機(jī)導(dǎo)航功能的輔助。用在高動(dòng)態(tài)飛行器上的GPS/慣性組合系統(tǒng)通常都是采用緊密組合模式。
偽距、偽距率組合原理:慣導(dǎo)系統(tǒng)輸出的位置和速度信息結(jié)合GPS給出的星歷數(shù)據(jù),可以求出相應(yīng)的偽距、偽距率。將計(jì)算得到的偽距、偽距率與GPS測量得到偽距、偽距率的之差作為量測值,通過卡爾曼濾波器估計(jì)慣導(dǎo)系統(tǒng)和GPS的誤差量,然后對(duì)兩個(gè)系統(tǒng)進(jìn)行反饋校正。
與位置、速度組合相比,基于偽距、偽距率的組合導(dǎo)航系統(tǒng)具有如下優(yōu)點(diǎn):1)直接采用了的原始觀測量偽距、偽距率,無量測相關(guān)問題,并考慮了GPS接收機(jī)誤差模型,可以獲得更高的組合精度[6]。2)當(dāng)GPS有效星數(shù)小于4時(shí),仍可提供優(yōu)于純慣性的導(dǎo)航精度,具有一定的可靠性和容錯(cuò)性;當(dāng)有效星數(shù)大于4時(shí),通過數(shù)據(jù)冗余可以進(jìn)一步提高精度。3)慣性導(dǎo)航系統(tǒng)具有較高的短期位置精度和速度精度,利用這些信息輔助GPS的接收和跟蹤過程,可以提高GPS的定位精度、動(dòng)態(tài)性能和抗干擾能力。
2 卡爾曼濾波器的設(shè)計(jì)
2.1 狀態(tài)方程
卡爾曼濾波器的設(shè)計(jì)是SINS/GPS緊密組合導(dǎo)航的關(guān)鍵,卡爾曼濾波器的狀態(tài)模型主要依據(jù)系統(tǒng)的誤差模型,包含慣導(dǎo)誤差模型和接收機(jī)誤差模型,由于為解決鐘差突跳問題采用了量測雙差方式,去掉了接收機(jī)鐘差對(duì)量測值的影響。故狀態(tài)方程中不包含接收機(jī)鐘差項(xiàng),僅含慣導(dǎo)誤差模型,SINS誤差模型參考文[7],包括速度誤差、姿態(tài)和航向誤差、位置誤差、陀螺漂移和加速度計(jì)零偏15個(gè)狀態(tài)變量:
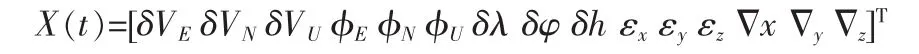
根據(jù)狀態(tài)變量X(t)和系統(tǒng)誤差模型可以得到偽距、偽距率組合的狀態(tài)方程:
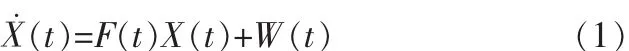
式中
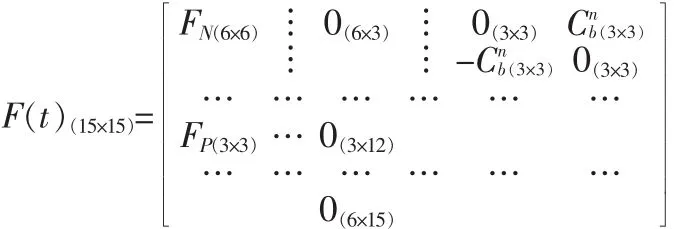
2.2 偽距量測值構(gòu)成
量測模型采用偽距組合方式。已知慣導(dǎo)系統(tǒng)解算的地理位置信息λ、φ、h,可求得地球坐標(biāo)系下的位置:

根據(jù)星歷給出的GPS衛(wèi)星軌道信息,可確定衛(wèi)星在地球坐標(biāo)系中的瞬時(shí)位置xsi、ysi、zsi,從而計(jì)算出慣導(dǎo)位置相對(duì)于衛(wèi)星i的偽距:

由此可得到相對(duì)衛(wèi)星i的偽距差值

上式中δρi可直接作為量測值進(jìn)行濾波計(jì)算。由于GPS接收機(jī)時(shí)鐘誤差引起的等效距離每秒遞增,當(dāng)GPS接收機(jī)長時(shí)間工作后,時(shí)鐘誤差累積到一定值,此時(shí)接收機(jī)將時(shí)鐘誤差清零,組合導(dǎo)航系統(tǒng)接收到的GPS測量偽距ρ0發(fā)生很大的跳變,進(jìn)而產(chǎn)生了奇異值。該奇異值引起卡爾曼濾波器錯(cuò)誤修正,導(dǎo)致濾波發(fā)散。
為解決這種現(xiàn)象,改用偽距量測差分方法。即從可見星中選擇仰角最大的衛(wèi)星m作為基準(zhǔn)星,慣導(dǎo)相對(duì)該衛(wèi)星m的偽距差值δρm=ρIm-ρGm為基準(zhǔn)值,進(jìn)一步構(gòu)成量測值為:
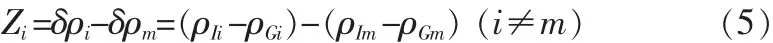
綜上所述,單個(gè)偽距量測值的量測方程為:

式中 Hρ(t)(1×15)=[0(1×6)…Hρ(1×3)…0(1×6)]

考慮噪聲 vρi和 vρm不相關(guān),則由量測噪聲 Vρ(t)值的構(gòu)成可知
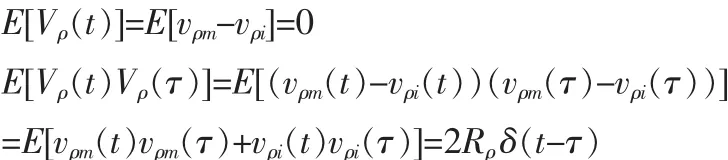
2.3 基于曲線擬合的量測預(yù)測算法
在高動(dòng)態(tài)環(huán)境下,由于載體運(yùn)動(dòng)參數(shù)的變化十分復(fù)雜,所以不可能用某一確定的函數(shù)來精確描述載體運(yùn)動(dòng)參數(shù),但是在很短的時(shí)間段內(nèi)可以用簡單曲線來分段擬合近似描述之。而每段的擬合曲線可以用導(dǎo)航系統(tǒng)輸出的當(dāng)前時(shí)刻、之前時(shí)刻的量測值以及量測更新周期T和延遲時(shí)間Δt來表示,一旦擬合曲線確定,就可以計(jì)算求得tk+Δt時(shí)刻導(dǎo)航系統(tǒng)的量測預(yù)測值 Zk+Δt。
假設(shè)在某個(gè)時(shí)刻tk+Δt獲得導(dǎo)航系統(tǒng)輸出的量測值Zk,該量測值帶有延遲量Δt,其所對(duì)應(yīng)的時(shí)刻是tk,意即Zk并不是tk+Δt時(shí)刻的量測值,而是tk時(shí)刻的量測值。并設(shè)導(dǎo)航系統(tǒng)在tk-1時(shí)刻的量測值為Zk-1,在tk-2時(shí)刻的量測值為Zk-2,其量測更新周期為T。為了便于說明,此處不妨采用拋物線來擬合預(yù)測導(dǎo)航系統(tǒng)的量測值。
在[tk-2,tk]時(shí)間段內(nèi),對(duì)導(dǎo)航系統(tǒng)輸出的量測值 Z(t)作以下擬合:
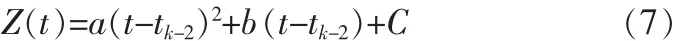
于是,每個(gè)量測更新時(shí)刻點(diǎn)所對(duì)應(yīng)的量測值之間的時(shí)序關(guān)系如圖1所示。
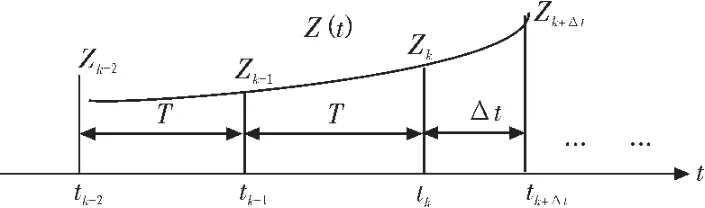
圖1 量測更新時(shí)刻點(diǎn)所對(duì)應(yīng)量測值之間的時(shí)序關(guān)系Fig.1 Timing relationship of measurement updates and measure value
對(duì)于 tk-2、tk-1、tk時(shí)刻,它們所對(duì)應(yīng)的量測值 Z(t)分別為 Zk-2、Zk-1、Zk,即
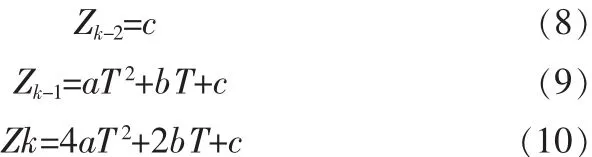
聯(lián)立式(8)、(9)和(10),可以求得

于是,根據(jù)式(7)和(11)可計(jì)算出 tk+Δt時(shí)刻導(dǎo)航系統(tǒng)的量測預(yù)測值 Zk+Δt為
從而,根據(jù)導(dǎo)航系統(tǒng)輸出的當(dāng)前時(shí)刻量測Zk、前兩個(gè)時(shí)刻量測Zk-1和Zk-2、量測更新周期T和延遲時(shí)間Δt,就可以遞推計(jì)算求得tk+Δt時(shí)刻導(dǎo)航系統(tǒng)的量測預(yù)測值Zk+Δt。然后,利用該量測預(yù)測值與tk+Δt時(shí)刻慣導(dǎo)系統(tǒng)的輸出參數(shù)進(jìn)行組合導(dǎo)航卡爾曼濾波計(jì)算,從而獲得當(dāng)前時(shí)刻系統(tǒng)誤差狀態(tài)的最優(yōu)估計(jì)值。
上述基于曲線擬合的量測預(yù)測算法采用的是拋物線來擬合預(yù)測導(dǎo)航系統(tǒng)的量測值,根據(jù)不同的載體飛行動(dòng)態(tài)和精度要求,還可以選取其他曲線來擬合預(yù)測導(dǎo)航系統(tǒng)的量測值,如直線、三次拋物線等,拋物線的階次越高,擬合的精度越高,但計(jì)算量也越大。
3 仿真驗(yàn)證
為了驗(yàn)證前面所提出的基于曲線擬合的量測預(yù)測算法,以SINS/GPS組合導(dǎo)航系統(tǒng)為對(duì)象,分別對(duì)直接采用滯后量測的組合導(dǎo)航和采用量測預(yù)測的組合導(dǎo)航進(jìn)行了仿真研究。
其中,GPS輸出更新周期為1 s,輸出延遲時(shí)間為100 ms。卡爾曼濾波周期為1s,仿真時(shí)間仍為1 500 s。基于上述仿真條件,首先對(duì)直接采用滯后量測的SINS/GPS組合導(dǎo)航進(jìn)行計(jì)算機(jī)仿真,仿真結(jié)果如圖2、圖3所示。
根據(jù)圖2~3可以看出,在完全相同的導(dǎo)航系統(tǒng)精度條件下,GPS量測輸出滯后嚴(yán)重影響了SINS/GPS組合導(dǎo)航的結(jié)果:在直接采用滯后量測進(jìn)行組合導(dǎo)航時(shí),載體東向速度誤差最大達(dá)到1.32 m/s,北向速度誤差最大達(dá)到1.58 m/s,天向速度誤差最大達(dá)到3.92 m/s;而緯度誤差最大達(dá)到93 m,經(jīng)度誤差最大達(dá)到115 m,高度誤差最大達(dá)到118 m。顯然,量測滯后時(shí)的SINS/GPS組合導(dǎo)航精度很不理想,說明GPS量測輸出滯后給組合導(dǎo)航結(jié)果帶來了很大的誤差。

圖2 量測滯后時(shí)的SINS/GPS組合導(dǎo)航速度誤差Fig.2 Velocity error of SINS/GPS integrated navigation system based on measurement delay
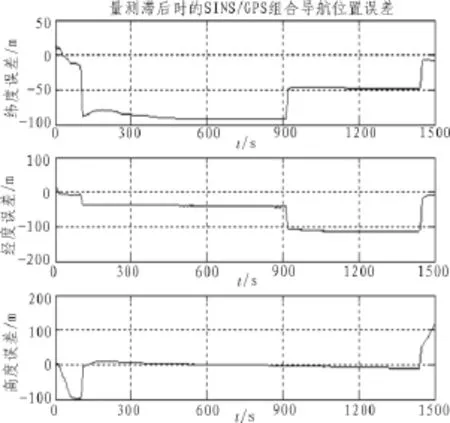
圖3 量測滯后時(shí)的SINS/GPS組合導(dǎo)航位置誤差Fig.3 Position error of SINS/GPS integrated navigation system based on measurement delay
接著,在與上面相同的仿真條件下,采用文中提出的基于曲線擬合的量測預(yù)測算法對(duì)SINS/GPS組合導(dǎo)航進(jìn)行計(jì)算機(jī)仿真,仿真結(jié)果如圖4、圖5所示。
根據(jù)圖4~5可以看出,在相同的仿真條件下,采用量測預(yù)測后的SINS/GPS組合導(dǎo)航獲得了較為滿意的結(jié)果:經(jīng)過1 500 s的仿真時(shí)間,東向、北向、天向速度誤差最終穩(wěn)定在0.05 m/s以內(nèi);緯度誤差控制在8 m以內(nèi),經(jīng)度誤差控制在6 m以內(nèi),高度誤差則控制在8.5 m以內(nèi)。
4 結(jié) 論
本文針對(duì)工程實(shí)踐中SINS/GPS緊密組合導(dǎo)航系統(tǒng)在進(jìn)行信息融合時(shí),因?yàn)榻邮諜C(jī)輸出的導(dǎo)航信息的延時(shí),直接影響導(dǎo)航系統(tǒng)濾波效果的問題,提出了基于曲線擬合的SINS/GPS緊密組合導(dǎo)航系統(tǒng)解決這一問題。通過采用本文所提出的基于曲線擬合的量測預(yù)測算法能夠有效地解決導(dǎo)航系統(tǒng)量測滯后的問題,而且該算法計(jì)算相對(duì)簡單、獨(dú)立,只利用到導(dǎo)航系統(tǒng)當(dāng)前時(shí)刻和之前兩個(gè)時(shí)刻的量測信息,不僅計(jì)算量小,還能夠較好地適應(yīng)高動(dòng)態(tài)環(huán)境和高精度要求,特別適用于解決諸如GPS和北斗這種量測更新頻率高、量測滯后時(shí)間短的導(dǎo)航系統(tǒng)的量測滯后問題。
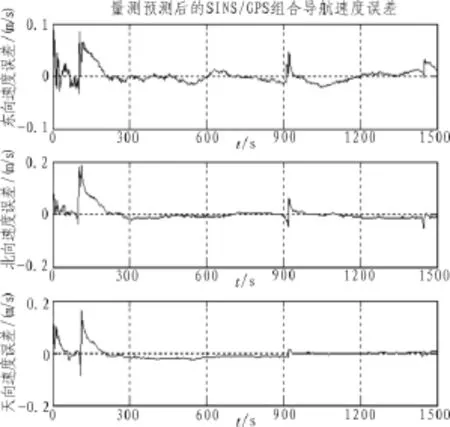
圖4 量測預(yù)測后的SINS/GPS組合導(dǎo)航速度誤差Fig.4 Velocity error of SINS/GPS integrated navigation system after measurement forecast
[1]秦永遠(yuǎn),張洪,王淑華.卡爾曼濾波與組合導(dǎo)航原理[M].西安:西北工業(yè)大學(xué)出版社,1998.
[2]于潔,王新龍.SINS/GPS緊密組合導(dǎo)航系統(tǒng)仿真研究[J].航空兵器,2008(6):8-13.
YU Jie,WANG Xin-long.Simulation of SINS/GPS tightly coupled integrated navigation system[J].Aero Weaponry,2008(6):8-13.
[3]李倩,占星群,王立端,等.GPS/INS組合導(dǎo)航系統(tǒng)時(shí)間同步系統(tǒng)設(shè)計(jì)[J].傳感技術(shù)學(xué)報(bào),2009,22(12):1752-1756.
LI Qian,ZHAN Xing-qun,WANG Li-rui,et al.Time synchronizer design in integrated GPS/INS system[J].Chinese Journal of Sensors and Actuators,2009,22(12):1752-1756.
[4]劉建業(yè),熊智,段方.考慮量測滯后的INS/SAR組合導(dǎo)航非等間隔濾波算法研究 [J].宇航學(xué)報(bào),2004,25(6):626-631.
LIU Jian-ye,XIONG Zhi,DUAN Fang.Processing the measurementdelay INS/SAR integrated navigation incoordinate interval filtering algorithm study[J].Journal of Astronautics,2004,25(6):626-631.
[5]Lee Hyung Keun,Lee Jang Gyu,Jee Gyu-In.Effect of GPS measurement delay on SDINS[C]//In:IEEE Position Location and Navigation Symposium, San Diego, CA,2000:464-471.
[6]QI Hong-hui,Moore J B.Direct kalman filtering approach for GPS/INS integration[J].IEEE Trans on AES,2002,38(2):687-693.
[7]袁信,俞濟(jì)祥,陳哲.導(dǎo)航系統(tǒng)[M].北京:航空工業(yè)出版社,1993.

