計算多自由度彈性體系的最大地震反應
楊曉云 楊衛平 谷明宇
(1.內蒙古科技大學建筑與土木工程學院,內蒙古包頭 014010; 2.內蒙古科技大學礦業工程學院,內蒙古包頭 014010)
0 引言
目前,對結構抗震設計最有意義的是結構最大地震反應。兩種計算多自由度彈性體系最大地震反應的方法:一種是振型分解反應譜法,另一種是底部剪力法。其中前者的理論基礎是地震反應分析的振型分解法及地震反應譜概念,而后者則是振型分解反應譜法的簡化。
1 振型分解法求解框架的最大底部剪力和最大頂點位移
3層剪切型結構如圖1所示,結構處于8度區(地震加速度是0.20g),Ⅰ類場地第一組,結構阻尼比是0.05。試采用振型分解反應譜法,求結構在多遇地震下的最大底部剪力和最大頂點位移。

解:該結構是3自由度體系,質量矩陣和剛度矩陣分別為:
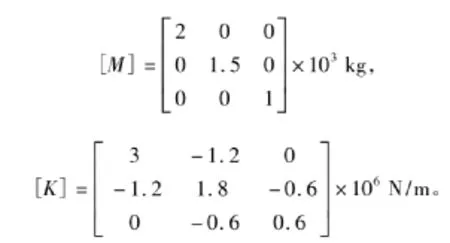

即:B3-5.5B2+7.5B-2=0。
由上式可得:B1=0.351,B2=1.61,B3=3.54。


為求第一階振型,將w1=14.5rad/s代入:

得

則第一階振型為:

同理得:


根據場地類別、設計地震分組查表得特征周期值:

根據設防烈度、地震影響查表得水平地震影響系數:αmax=0.16,則:

由Fji=Giαjγjφji得:
第一振型各質點(或各樓面)水平地震作用為:
F11=2.0×9.8×0.0976×1.421×0.301=0.818kN。F12=1.5×9.8×0.0976×1.421×0.648=1.321kN。

第二振型各質點(或各樓面)水平地震作用為:

第三振型各質點(或各樓面)水平地震作用為:

則由各振型水平地震作用產生的底部剪力為:
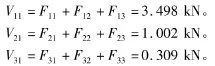
通過振型組合求結構的最大底部剪力為:

若僅取前兩階振型反應進行組合,則:

由各振型水平地震作用產生的結構頂點位移為:

通過振型組合求結構的最大頂點位移為:

若取前兩階振型反應進行組合:

由上述計算可總結:結構的低階振型反應大于高階振型反應,振型階數越高,振型反應越小。因此,結構的總地震反應以低階振型反應為主,而高階振型反應對結構總地震反應的貢獻較小。故求結構總地震反應時,不需要取結構的全部振型反應進行組合。通過統計分析,振型反應的組合數可按如下規定確定:1)一般情況下,可取結構前2階~3階振型反應進行組合,但不多于結構自由度數。2)當結構基本周期T1>1.5s時或建筑高寬比大于5時,可適當增加振型反應的組合數。
2 底部剪力法求解框架的最大底部剪力和最大頂點位移
結構如圖1所示,采用底部剪力法,求結構在多遇地震下的最大底部剪力和最大頂點位移。
解:由上述計算已求得α1=0.0976,而結構總重力荷載為:

則結構的底部剪力為:

已知:Tg=0.25s,T1=0.433s>1.4Tg=0.35s。
設該結構為鋼筋混凝土房屋結構,則需考慮結構頂部附加集中作用。查表得:

則:ΔFn= δn FEK=0.105×3.659=0.384kN。
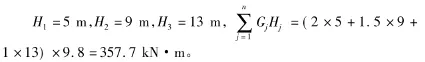
則作用在結構各樓層上的水平地震作用為:

由此得結構的頂點位移為:

與振型分解法的計算結果相比,可見底部剪力法的計算結果與振型分解反應譜法很接近。
說明:底部剪力法適用于重量和剛度沿高度分布均比較均勻的結構。當建筑物有局部凸出屋面的小建筑物(如屋頂間,女兒墻,煙囪)等時,由于該部分結構的重量和剛度突然變小,將產生鞭梢效應,即局部凸出小建筑的地震反應有加劇的現象。因此,當采用底部剪力法計算這類小建筑的地震作用效應時,計算按式作用在小建筑上的地震作用需乘以增大系數,抗震規范規定該增大系數取為3。但是,應注意鞭梢效應只對局部凸出小建筑有影響,因此作用在小建筑上的地震作用向建筑主體傳遞時或計算建筑主體的地震作用效應時,則不乘增大系數。
3 結語
采用振型分解反應譜法計算結構最大地震反應精度較高,一般情況下無法采用手算,必須通過計算機計算,且計算量較大。理論分析表明,當建筑物高度不超過40m,結構以剪切變形為主且質量和剛度沿高度分布較均勻時,結構的地震反應將以第一振型反應為主,而結構的第一振型接近直線,此時可用底部剪力法簡化計算。
[1]劉昭培,張韞美.結構力學(下冊)[M].第4版.天津:天津大學出版社,2000.
[2]張延慶.結構力學(下冊)[M].北京:科學出版社,2006.
[3]R·W·克拉夫,J·彭津.結構力學[M].北京:科學出版社,1981.
[4]李國強,李 杰,蘇小卒.建筑結構抗震設計[M].北京:中國建筑工業出版社,2009.

