不同病害情況下盾構隧道環向剛度的計算方法

李春良，王 勇，王 旭

(1.吉林建筑大學交通科學與工程學院，吉林長春 130118;2.吉林省公路管理局，吉林長春 130021)

0 引言

隨著使用時間的增長，許多盾構隧道的襯砌結構出現了不同程度的損壞，如襯砌結構的開裂、變形、掉塊，滲水及材料的劣化等，其中襯砌裂縫的出現是最主要的病害之一，它還會導致其他形式病害的發生。這些病害會影響盾構隧道結構的力學性能和安全性能，會降低管片環局部的剛度和變形能力。由于盾構隧道的管片環屬于超靜定結構，局部剛度的改變會導致整個管片環向內力重分布情況的發生。因此，在力學計算過程中，明確剛度的降低情況及剛度重分布問題是極為重要的。

目前，大多數學者對盾構隧道病害的研究主要集中在分析這些病害出現的原因及規律，并提出相應的加固養護措施［1－6］，也有部分學者對隧道病害的監測進行了研究［7－9］，而對盾構隧道出現相應病害后對管片結構損失后的剛度影響情況和剛度分布問題方面的研究并不多。近年來，國內有少數學者對無病害的管片縱向剛度進行了研究［10－12］。如能將管片環中隨機離散的接縫或缺陷用統一的剛度模型表示，則能較為方便地描述隧道環向剛度的變化及對隧道環內力的影響情況，對今后認清隧道的內力重新分布問題及加固維修是極為重要的。本文針對盾構隧道幾種病害出現后的特點，建立相應的剛度模型，并計算出管片環出現相應病害后的環向剛度分布情況。

1 常見盾構隧道病害

1.1 襯砌裂縫

管片裂縫對盾構隧道的安全及耐久性影響較大，會引起隧道漏水和滲水，影響盾構隧道的使用功能和其他設施的安全。如果不及時處理，將會產生嚴重的后果。產生裂縫后的管片結構裂縫部位的剛度會降低，會引起管片的內力分布發生變化。

1.2 漏水

盾構隧道出現裂縫后，常會發生漏水現象，影響隧道的穩定性、安全性和洞內設施的正常使用。如果滲水時間較長，還容易引起襯砌混凝土結構剝落及風化，最終使鋼筋銹蝕膨脹導致混凝土襯砌管片的大面積開裂，降低襯砌的承載能力，嚴重威脅到管片結構的安全。另外，管片壁后其他區域的地下水還會向滲水部位遷移，壁后一部分土顆粒會被滲水沖蝕掏空，在管片壁后土層中形成空洞，與周圍地層脫離，并形成巨大水壓力，影響圍巖和管片的穩定性，威脅到隧道的安全。

1.3 混凝土碳化與鋼筋的銹蝕

盾構隧道在使用一定年限后，混凝土材料的管片會發生一定程度的碳化。混凝土碳化后會引起管片結構的表面損壞，加快內部鋼筋的銹蝕，產生銹蝕裂縫，導致結構漏水和剛度降低，承載能力不足造成結構變形過大，影響隧道的使用壽命。

1.4 混凝土剝離

混凝土管片在長期使用下，由于受到各種不利因素的影響，會導致部分區域一定厚度的混凝土層剝落，造成粗骨料外露的現象，嚴重時還會造成骨料松脫，使局部管片厚度變薄，降低管片局部剛度，影響承載。

1.5 凍害

在北方嚴寒地區，由于溫度低，部分隧道常受到凍融作用的影響而出現襯砌凍脹開裂、酥碎、剝落、漏水及掛冰等現象，使部分隧道難以發揮正常使用功能，最終導致襯砌劣化。

2 盾構隧道管片環向剛度模型

盾構的主要承力構件是襯砌，它由若干預制鋼筋混凝土管片或砌塊通過接頭連接拼裝而成［8］。各接頭處能承受一定比例的彎矩，但該部位并非完全剛接，也并非完全鉸接，它破壞了管片環向剛度的等值連續性。同時，環向接頭部位的抗彎能力要比無接頭的位置處削弱很多。在盾構隧道力學計算過程中，如何將這種環向剛度分布的不均勻性反映到設計計算過程中是至關重要的，它決定了設計計算的安全性。為準確地揭示出各類病害對盾構隧道環向受力的影響，必須先建立無病害情況下的管片環向剛度分布模型。管片環結構示意見圖1。

圖1 管片環結構示意圖Fig.1 Structure of segment ring

由上文分析可知，管片接頭部位可以承受一定比例的彎矩。圖1中管片環存在若干個接頭，設無接頭部位管片橫截面的完整抗彎剛度為E1I1;接頭的存在導致管片環在接頭部位抗彎剛度下降，在接頭部位設管片環抗彎剛度的損失效率為ξ，管片環在接頭部位損失的抗彎剛度為ξE1I1，則管片環在接頭部位最終剩余的有效抗彎剛度為(1－ξ)E1I1。為了得到管片在環向各位置處的抗彎剛度環向分布模型，取第i個管片接頭并將其局部放大，如圖1所示。

2.1 接頭部位損失的抗彎剛度公式

為研究方便，在環向將管片環在第i個接頭，di位置處損失的抗彎剛度展開為級數形式，其表達式為

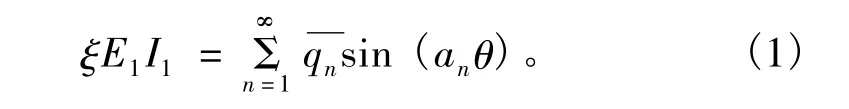
在式(1)中，an=n/2，而

經整理，管片環在接頭di處損失的抗彎剛度

2.2 帶裂縫部位損失的抗彎剛度公式

管片環在第j條裂縫部位的抗彎剛度會下降，設在裂縫部位管片環抗彎剛度的損失效率為ξ'，根據上述過程可以得到帶裂縫部位損失的抗彎剛度

2.3 局部混凝土剝落損失的抗彎剛度公式

管片環在第L個局部混凝土脫落部位的抗彎剛度會下降，設在混凝土脫落部位管片環抗彎剛度的損失效率為ξ″，根據上述過程可以得到局部混凝土剝落損失的抗彎剛度

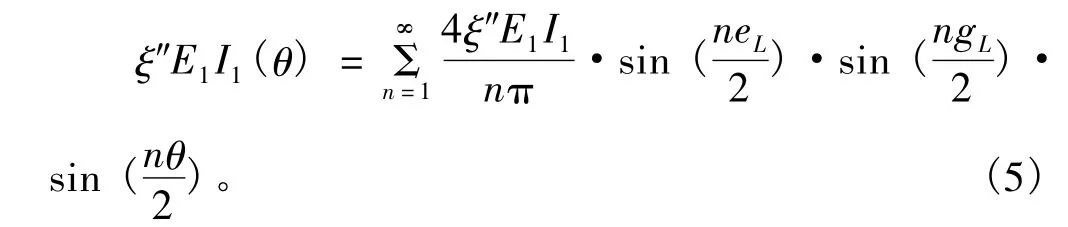
2.4 管片環變剛度公式

根據傅立葉級數關系，將抗彎剛度為E1I1的均勻圓環的剛度模型可以展開成以下級數形式:

由于管片環在環向各位置處的有效抗彎剛度為均勻環剛度與接頭部位損失剛度之差，則根據式(3)—(6)可以建立管片在環向各位置截面處不均勻的連續剛度模型為

式(7)為帶病害管片環向抗彎剛度模型，能夠考慮到接頭、管片環向開裂和管片混凝土大面積剝落等病害所導致的抗彎剛度降低問題。在計算實際問題時，可以根據實際病害的類型，對式(7)進行適當地舍取。對于發生材料劣化時，只需將式(7)中的E1I1值進行調整。

3 算例

為驗證文中建立的管片環剛度分布模型的正確性與合理性，結合實際的管片結構進行計算，并與實際情況進行對比。

3.1 算例簡介

混凝土管片 E=3.45 ×107kPa，外徑為6.2 m，內徑為5.5 m，厚度為0.35 m。取I型管片和II型管片，分塊情況為:84 °×1，64°×4，16°×1;67.5°×3，68.75°×2，20°×1。管片環分塊見圖2。

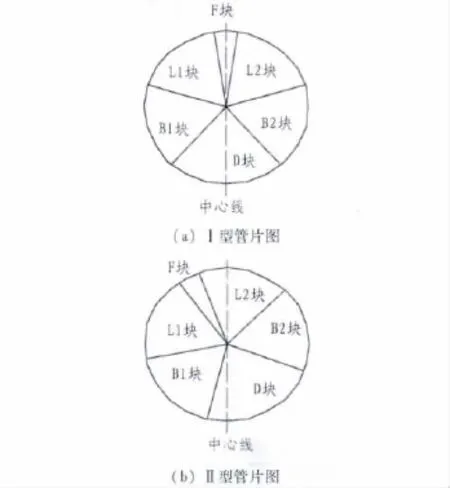
圖2 管片環分塊示意圖Fig.2 Division of segment ring

3.2 計算結果

3.2.1 管片環向抗彎剛度計算結果

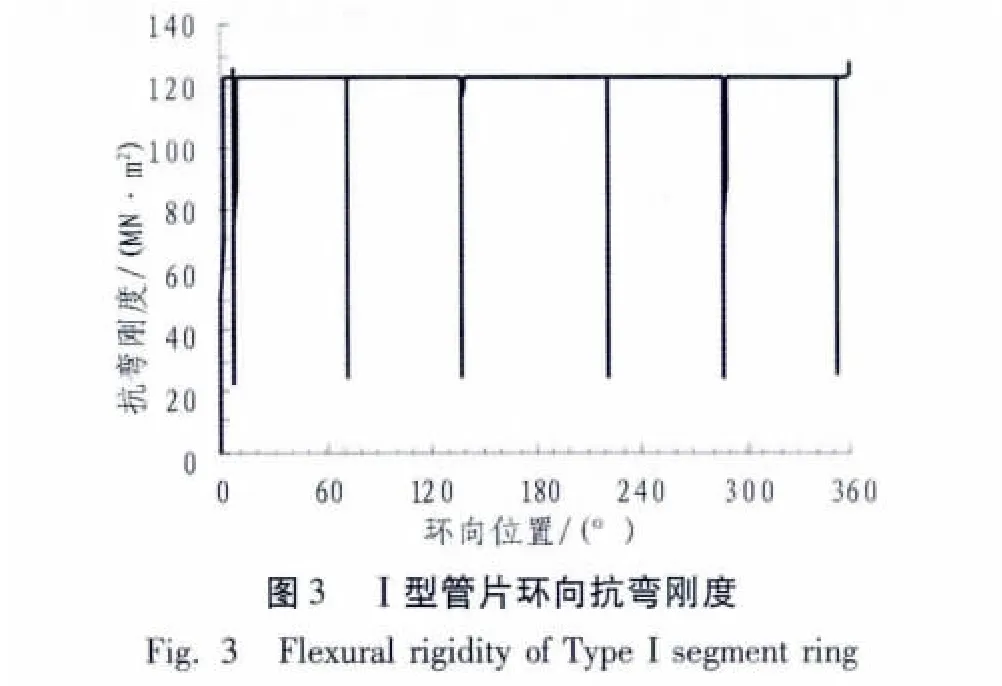
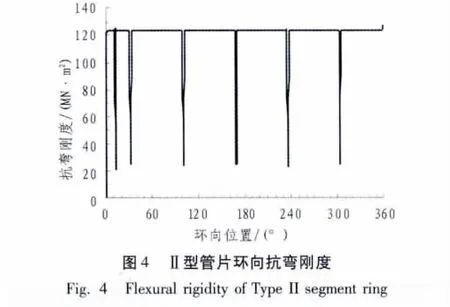
根據管片環向抗彎剛度計算模型，取接頭抗彎剛度損失效率為80%，分別計算算例中I型管片和II型管片環的環向剛度分布情況規律，計算結果如圖3和圖4 所示。在圖 2(a)中，環向 8°，73°，138°，222°，287°，352°位置處計算得到的抗彎剛度值均發生突變降低。在圖 2(b)中，環向 12.5°，32.5°，101.25°，168.75°，236.25°，303.75°位置處計算得到的抗彎剛度值均發生突變降低。主要由于I型管片在8°，73°，138°，222°，287°，352°位置處設有接頭;II 型管片在12.5°，32.5°，101.25°，168.75°，236.25°，303.75°位置處設有接頭，進而導致結構的抗彎剛度發生突變，表明本文所建立的剛度分布模型是科學和合理的。

3.2.2 混凝土管片開裂后環向抗彎剛度計算結果

以I型管片為例，采用文中提供的裂縫剛度計算公式計算在30°，45°，60°位置處出現3條裂縫后的整體剛度分布情況。管片開裂后環向抗彎剛度如圖5所示。

由圖5可知，除在環向各接頭部位處的抗彎剛度值均發生突變降低，在環向 30°，45°，60°位置處的抗彎剛度值也發生突變，降低幅度達到50%左右。主要原因是 I型管片在30°，45°，60°位置處已經發生開裂，這些突變位置均與實際相符，表明本文所建立的剛度分布模型是正確合理的。

3.2.3 局部混凝土剝落后對管片環的內力影響

以I型管片為例，采用文中建立的局部混凝土剝離后的剛度計算公式，計算了在45°位置處，出現環向周長約0.58 m的混凝土脫落后的整體剛度分布情況。管片混凝土脫落后環向抗彎剛度如圖6所示。

在圖6中，除在環向各接頭部位處的抗彎剛度值均發生突變降低，在環向45°位置處環向周長約0.58 m的抗彎剛度值也發生突變降低。主要原因是I型管片在45°位置處混凝土脫落造成的抗彎剛度降低，降低程度達到67%左右，這些突變位置均與實際相符，表明本文所建立的剛度分布模型是正確合理的。

圖6 管片混凝土脫落后環向抗彎剛度結果Fig.6 Flexural rigidity of segment ring after concrete peeling

4 結論與討論

1)本文將管片環中隨機離散的接縫或缺陷用傅里葉級數進行數學建模，對于描述隧道環向剛度的變化及今后進一步采用解析方法推導其對隧道環內力的影響具有一定的應用價值。

2)本文建立了盾構隧道管片環在有、無病害情況下的剛度整體化模型，模型計算結果與實際相符，表明本文所建立的剛度分布模型是科學合理的。

3)本文建立的管片環整體剛度分布模型能夠有效避免在今后對管片環進行分析內力時，在剛度的突變位置將管片環依次劃分進行分析，簡化了內力計算程序，方便了后續深入研究管片破壞后的內力重新分布問題。

需要指出的是，文中所建立的剛度分布模型形式為傅里葉級數形式，對于涉及到高次積分求解時不容易求出方程顯示解。另外，由于本文建立的計算模型在處理剛度損失率時不可避免地采取了一些假設和簡化，在計算時會帶有一定的誤差，故如何較準確地確定文中假定的剛度修正系數尤為重要，該剛度修正系數決定了最終的計算精度。在后續的研究中，一方面需要深入研究修正系數的準確取值問題，另一方面還應該將本文建立的剛度整體化模型引入到對管片環剛度內力的計算中。

［1］ 袁超，李樹忱，李術才，等.寒區老舊隧道病害特征及治理方法研究［J］.巖石力學與工程學報，2011(S1):3354－3361.(YUAN Chao，LI Shuchen，LI Shucai，et al.Study of defects characteristics and repair methods of old tunnel in cold region［J］.Chinese Journal of Rock Mechanics and Engineering，2011(S1):3354 －3361.(in Chinese))

［2］ 馮沁銘.某鐵路隧道病害成因及其處治措施的探討［J］.山西建筑，2011(35):176 －178.(FENG Qinming.On exploration of reasons for diseases in some railway tunnel and their treatment measures［J］.Shanxi Architecture，2011(35):176 －178.(in Chinese))

［3］ 李彬，雷明鋒，李文華.運營公路隧道病害對襯砌結構安全性的影響［J］.鐵道科學與工程學報，2011(5):40－45.(LI Bin，LEI Mingfeng，LI Wenhua.Safety influence of operating highway tunnel caused by sturcture disease［J］.Journal of Railway Science and Engineering，2011(5):40 －45.(in Chinese))

［4］ 劉海京，鄭佳艷，程崇國，等.大坂山隧道病害處治工程工藝設計與實證分析［J］.重慶大學學報:自然科學版，2012(12):138 － 143.(LIU Haijing，ZHENG Jiayan，CHENG Chongguo，et al.Rehabilitation project of the Dabanshan highland road tunnel［J］.Journal of Chongqing University:Natural Science，2012(12):138 －143.(in Chinese))

［5］ 趙華.晉陽高速公路隧道滲水原因分析及處治方案［J］.山西建筑，2011(28):170 －171.(ZHAO Hua.On analysis of reasons for water leakage of tunnels along Jin-Yang expressway and its treatment scheme［J］.Shanxi Architecture，2011(28):170 －171.(in Chinese))

［6］ 李彬.偏壓隧道病害特征及其控制措施［J］.鐵道科學與工程學報，2011(6):59 －63.(LI Bin.Study on disease characteristics of unsymmetrcial pressure tunnel and its control measures［J］.Journal of Railway Science and Engineering，2011(6):59 －63.(in Chinese))

［7］ 張守成，關惠平，寇智勇，等.監控量測技術在公路隧道病害反演分析中的應用［J］.成都大學學報:自然科學版，2010(1):101 －107.(ZHANG Shoucheng，GUAN Huiping，KOU Zhiyong，et al.Application of monitoring measurement in inverse analysis of highway tunnel’s defects［J］.Journal of Chengdu University:Natural Science，2010(1):101 －107.(in Chinese))

［8］ 康富中，江波，賀少輝，等.地質雷達在風火山隧道病害檢測中的應用與結果分析［J］.工程地質學報，2010(6):51 －60.(KANG Fuzhong，JIANG Bo，HE Shaohui，et al.Detection and analysis of tunnel defects with geological penetrating radar at Fenghuo mountain ［J］.Journal of Engineering Geology，2010(6):51 －60.(in Chinese))

［9］ 王哲龍，王起才.探地雷達在隧道病害檢測中的應用［J］.水利與建筑工程學報，2009(4):123－125.(WANG Zhelong，WANG Qicai.Using of ground-sounding radar in tunnel disease detection［J］.Journal of Water Resources and Architectural Engineering，2009(4):123 －125.(in Chinese))

［10］ 鐘小春，張金榮，秦建設，等.盾構隧道縱向等效彎曲剛度的簡化計算模型及影響因素分析［J］.巖土力學，2011(1):132 －136.(ZHONG Xiaochun，ZHANG Jinrong，QIN Jianshe，et al.Simplified calculation model for longitudinal equivalent bending stiffness of shield tunnel and its influence factors’analysis［J］.Rock and Soil Mechanics，2011(1):132 －136.(in Chinese))

［11］ 張志強，朱敏，何川.盾構隧道縱向剛度計算方法以及影響因素研究［J］.現代隧道技術，2008(S1):24－28.(ZHANG Zhiqiang，ZHU Min，HE Chuan.Study on the factors of shield tunnel longitudinal rigidity calculation method and influence［J］.Modern Tunnelling Technology，2008(S1):24 －28.(in Chinese))

［12］ 葉飛，何川，朱合華，等.考慮橫向性能的盾構隧道縱向等效剛度分析［J］.巖土工程學報，2011(12):1870－1876.(YE Fei，HE Chuan，ZHU Hehua，et al.Longitudinal equivalent rigidity analysis of shield tunnel considering transverse characteristics［J］.Chinese Journal of Geotechnical Engineering，2011(12):1870 －1876.(in Chinese))