獅子洋隧道盾構對接方案的模糊判斷法

王連山，奚正平

(1.盾構及掘進技術國家重點實驗室，河南 鄭州 450001;2.中鐵隧道集團有限公司，河南 洛陽 471009;3.中鐵隧道股份有限公司，河南 鄭州 450001)

0 引言

隨著我國經濟和城市建設的快速發展，基礎設施工程建設中各種綜合問題日益突出，而模糊數學的出現與發展對許多領域，尤其是對工程技術領域產生了極大的影響［1］。與經典數學相比，模糊數學在分析復雜工程問題時更加顯示其優越性，因而近幾年發展非常迅速。模糊數學起源于1965年，由美國加利福尼亞州立大學的扎德教授創立［2］，解決了實際工程中無法精確計算或分析的問題。

在工程施工中，經常面臨施工方案選擇問題。對于不確定的質量、安全、工期、費用等影響因素，作為建設單位或施工企業，通常通過費用比較或工期比較進行選擇，而方案比較中對技術可行性、施工復雜程度和安全可靠性等問題，一般只能進行定性分析。為使方案選擇評價時盡可能定量化，運用模糊數學能解決該類問題。黃建光［3］應用模糊綜合評價模型對軌道交通設計方案進行評價，并得到設計方案的評價等級。馮玉坤［4］、趙彬［5］等人應用模糊數學模型對房屋建筑工程的造價估算進行研究。邵良杉等［6］對煤礦巷道工程造價進行數學模型研究，采用模糊數學中的貼近度等方法，得到擬建工程的造價。在盾構隧道施工中，盾構對接方案的選擇一般是根據經驗法進行比選。本文采用模糊數學判斷法對廣深港客運專線獅子洋隧道盾構對接方案進行定量分析，為今后施工方案定量分析及最優選擇提供參考。

1 模糊判斷法原理

用以確定使受控系統的給定性能指標取極大或極小值的最優控制方法，是最優控制理論的核心。在工程領域中，最優選擇問題也可采用極大值原理所提供的方法和原則來確定。模糊優化方法與普通優化方法的要求相同，仍然是尋求一個控制方案，滿足給定的約束條件，使目標函數為最優值;其區別僅在于模糊優化方法中包含模糊因素。普通優化可以歸結為求解一個普通數學規劃問題，模糊規劃則可歸結為求解一個模糊數學規劃(Fuzzy Mathematical Programming)問題，包含控制變量、目標函數和約束條件，其中控制變量、目標函數和約束條件可能都是模糊的，也可能某一方面是模糊的，而其他方面是清晰的。

假設f:X→R是有界函數，C∈F(X)，考慮f在C約束下的最大值問題，求解意味著既要最大限度地滿足約束，又要最大限度地達到理想目標，為此定義目標函數f:X→R是有界函數，C∈F(X)是模糊約束，令D=C∩Mf;Mf是函數f的無條件模糊優越集，稱D為f在C約束下的條件模糊優越集，稱f(D)為f在C約束下的條件模糊極大值，它們的隸屬函數分別為

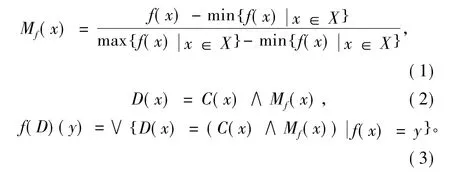
求解目標函數f(x)在模糊約束C下的條件極大值的3個步驟:

1)求無條件模糊優越集Mf;

2)求條件模糊優越集D=C∩Mf;

3)求條件最佳決策，即選擇x*，使

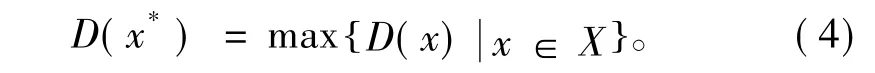
式中:x*是所求的條件極大點;f(x*)是在模糊約束C下的條件極大值。

采用上述模糊判斷法原理，可對土木工程施工方案的決策進行定量分析。對于盾構對接方案，目前僅日本在東京灣采用了機械對接技術，而我國對接技術尚處于空白狀態。現通過項目工程調研，采用模糊判斷法對廣深港客運專線獅子洋隧道盾構對接施工方案進行分析和比較。

2 獅子洋隧道盾構對接方案

獅子洋隧道位于廣深港鐵路客運專線東涌站至虎門站區間，為全線控制性工程。隧道采用雙孔單線結構，設計速度為200 km/h及以上，最小曲線半徑7 000 m，最大坡度20‰。盾構掘進通過粉質黏土、淤泥質黏土、細砂、中砂、粗砂、全風化至弱風化泥質砂巖、粉砂巖和細砂巖等多種復合地層，地下水豐富，與珠江水有一定的水力聯系，具弱承壓水頭，強承壓水占41%。

隧道全長10.8 km，分為 SDⅡ、SDⅢ2個標段，分左右線相向推進，在江中對接。襯砌管片采用鋼筋混凝土平板形管片，通用楔形環雙面楔形(楔形量24 mm)，管片厚500 mm，采用“7+1”分塊模式，環寬2.0 m。

隧道采用4臺直徑11.18 m氣壓調節式泥水平衡盾構，水深26.6 m，設計水壓達0.67 MPa。為確定合理的盾構對接施工方案，補充勘察了對接區域的地質情況。對接區域巖性為泥質粉砂巖，強度 10～25 MPa，滲透系數0.21 m/d。根據對接區域地質情況，采用離心實驗模型模擬了圍巖強度在10 MPa、巖體厚度為2.5 m、壓力為0.3 MPa情況下巖墻的穩定性。模擬實驗顯示，巖墻具有一定的穩定性［7］。

盾構對接目前有土木對接與機械對接2種方式［8］。日本東京灣隧道采用了機械對接方式［9］。根據獅子洋隧道對接區域地質補充勘探情況，對接方案既可選擇機械對接，也可選擇土木對接。

3 方案分析

盾構在海底對接施工中具有一定的風險性。對接方案是否合理直接影響工程成敗。如果對接不成功，將造成隧道涌水、海底坍塌、隧道被淹等工程事故。對接方案的比較如下:

1)機械對接。機械式盾構對接法通過在2臺盾構的前緣設置對接裝置，有效解決對接難題。雖然機械式對接施工對設備要求高，但是對接不需要進行地層加固，或僅需要進行小范圍的地層加固即可，因此施工質量高、操作簡單、風險低、安全性高，但由于設備的特殊設計與加工，設備費用引起的施工成本較高。另外，采用機械式盾構對接方案時，需要對貫通精度及盾構姿態有很好地控制，以保證成功對接。

2)土木地層加固對接。此方案對施工設備制造的相關要求低，使設備的制造工藝簡化，對工程施工更加有利，在獅子洋隧道施工圖設計中即采用此對接方案。制造商沿中盾圓周方向均勻布置了22個超前注漿孔(傾角13°，孔徑100 mm)，該孔既可用于超前注漿，又可利用注漿管作為超前支護。施工圖設計分別在左、右線DIK38+250～+100、DIK38+500～+550段對接，對接處為泥質粉砂巖和細砂巖地層，滲透性高，水壓在0.7 MPa左右。如果采用該對接方案，施工質量一般，風險性一般(帷幕注漿的可靠性決定了隧道涌水涌泥的風險)，施工安全性較高(采用超前錨桿預支護作為輔助施工措施)，計劃工期5個月。

3)土木直接掘進對接。土木直接掘進對接是在2臺盾構相向掘進相抵后，開倉將2臺盾構的切口環采用聯接鋼板焊接聯通成整體，在盾殼的保護下，拆除盾殼內部設備構件，再施工鋼筋混凝土襯砌的施工方法［10］。采用土木直接掘進對接，設備可直接采用常規設備。與機械對接、土木地層加固對接一樣，采用土木直接掘進對接，盾殼需要設計為雙盾殼，不需要地層加固。采用土木直接掘進對接，施工安全與質量一般，但操作簡單，且在這3種方案中成本最低。但是，采用土木直接掘進對接，需要對接區域的地層具有強穩定性及弱透水性。地質勘察顯示，DK37+800～+850段主要為弱風化泥質粉砂地層;離心模型實驗研究顯示，該段圍巖具有一定的穩定性，滲透系數0.21 m/d，滿足土木直接掘進對接要求。采用土木直接掘進對接，可節約地層加固時間，工期可提前1個月左右。

從上述方案比較來看，3種方案各有利弊。為了對上述3種方案進行定量分析，應用模糊約束下的條件極值來求解，將設備、地層加固、安全與質量等對施工有影響的因素作為模糊約束條件，把造價作為目標函數，即 X={x1(機械對接)，x2(土木地層加固對接)，x3(土木直接掘進對接)}。方案比較見表1。

表1 方案評價表Table 1 Program evaluation table

將真值語言轉化為各模糊約束集Ci∈F(X)(i=1，2，3，4，5)的隸屬度對應關系。對 C1，C2，Mf而言，對應關系見表2。

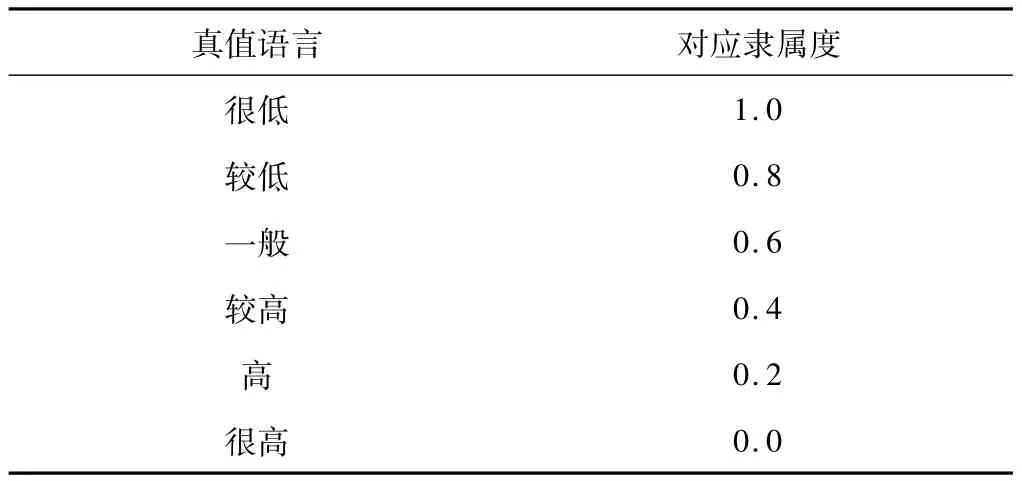
表2 C1，C2，Mf真值語言對應隸屬度關系Table 2 Membership relation of true value language of C1，C2and Mf

對C3，C4而言，對應關系見表3。

隸屬度真值語言轉化后見表4。

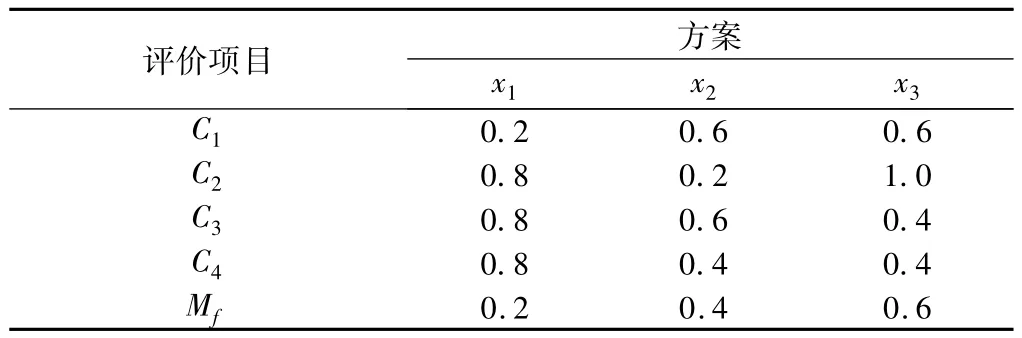
表4 真值語言與隸屬度函數轉化表Table 4 Conversion between true value language and membership function

計算模糊判決集

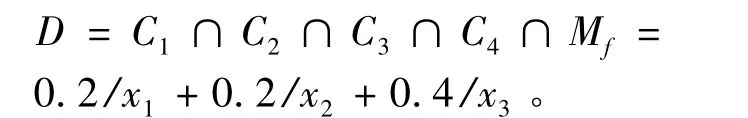
4 直接掘進對接方案控制措施及效果

4.1 控制措施

盾構直接掘進對接是在不采取任何地層加固措施、設備不具有機械對接裝置的情況下，2臺相向掘進的盾構直接掘進對接。因此，在施工中應做好以下控制措施:

1)提前準備好30 mm厚環形分塊鋼板，并在地面試拼接。盾構對接后，對刀盤對接處的盾構外殼切口環縫隙，采用準備好的環形鋼板聯接，使2臺盾構的外殼形成整體;

2)備好排水泵，發現漏水及時抽排;

3)做好地層監控，采用海底聲納等設備監測海底地層變化;

4)相向盾構掘進相距50 m時，建立通信聯系，及時通報盾構所處的空間位置;

5)通過盾構姿態調整，減少盾構對接誤差;

6)開倉前注意觀察液位變化情況，發現液位變化較快時，應做好壓力控制。

4.2 施工效果

2010年12月8日，獅子洋隧道左線2臺盾構順利對接。對接點圍巖相對穩定，安全性較好，掌子面殘留的碴土很少;相向對接精度平面偏差28.5 mm，高程偏差19.6 mm，滿足設計規定的貫通誤差在±50 mm以內的要求。現場刀盾對接見圖1，設備拆除見圖2，盾構外殼縫隙焊接見圖3。

繼左線成功對接之后，2011年3月11日，獅子洋隧道右線也成功采用直接掘進對接方式實現盾構對接。

獅子洋隧道左、右線2次順利對接是國內首次采用盾構法施工對接技術，開創了盾構地下直接掘進對接先河。

圖1 刀盤對接Fig.1 Shield docking

圖2 設備拆除Fig.2 Removal of equipment

圖3 盾構外殼縫隙焊接Fig.3 Welding of shield shell gap

與原設計土木地層加固對接方案相比，采用土木直接掘進對接施工方案，施工工期節約20 d之多，節約小導管及地層加固注漿等施工成本約107萬元。

5 結論與體會

在獅子洋隧道對接方案選擇過程中，采用模糊判斷法解決了施工方案選擇的量化確定問題，算法簡單，便于理解。采用模糊判斷法存在的問題是不能將所有影響因素都納入計算系統(否則計算量過大)，因此存在計算精確度偏差。

今后在類似施工方案選擇時，可將施工方案的影響因素進一步細化，例如增加地質因素、人員因素等，以提高計算精確度。

［1］ 長林.模糊數學法在建設工程項目中的應用思路研究［J］.南昌教育學院學報，2011，26(4):66－68.(CHANG Lin.Application of fuzzy math in the construction project［J］.Journal of Nanchang College of Education，2011，26(4):66－68.(in Chinese))

［2］ 賀仲雄.模糊數學及其應用［M］.天津:天津科學技術出版社，1983.

［3］ 黃建光.模糊數學在軌道交通工程設計方案比選中的應用［J］.石家莊鐵道學院學報:自然科學版，2010，23(1):74 －77.(HUANG Jianguang.Application of fuzzy mathematical theory in cityrailtransitprojectdesign optimization［J］.Journal of Shijiazhuang Railway Institute:Natural Science，2011，23(1):74－77.(in Chinese))

［4］ 馮玉坤，任憲儒，方修帥.模糊估算在工程造價中的應用［J］.青島建筑工程學院學報，2002，23(4):27－31.(FENG Yukun，REN Xianru，FANG Xiushuai.The application of rough estimate in the fabrication cost of project［J］.Journal of Qingdao Institute of Architecture and Engineering，2002，23(4):27－31.(in Chinese))

［5］ 趙彬.工程項目成本快速測算方法研究［J］.工程造價管理，2011，11(4):23－25.

［6］ 邵良杉，任滿杰，劉彥生.礦山井巷工程造價模糊測算模型［J］.阜新礦業學院學報:自然科學版，1995，14(1):108 － 111.(SHAO Liangshan，REN Manjie，LIU Yansheng.Themine shaftand lane engineering cost evaluation model［J］.Journal of Fuxin Mining Institute:Natural Science Edition，1995，14(1):108 － 111.(in Chinese))

［7］ 洪開榮.水下盾構隧道硬巖處理與對接技術［J］.隧道建設，2012，32(6):361－365.(HONG Kairong.Case study on hard rock treatment technology and shield docking technology in boring of underwater tunnels［J］.Tunnel Construction，2012，32(6):361－365.(in Chinese))

［8］ 陳饋，洪開榮，吳學松.盾構施工技術［M］.北京:人民交通出版社，2009.

［9］ 王國安.盾構地中對接施工技術初探［J］.隧道建設，2007，27(8):536 －541.(WANG Guo’an.Preliminary studyon construction technology ofconnecting shield Machines in the ground［J］.Tunnel Construction，2007，27(8):536－541.(in Chinese))

［10］ 洪開榮.高速鐵路水下盾構隧道結構力學特征及掘進與對接技術研究［D］.北京:北京交通大學土木建筑工程學院，2011.(HONG Kairong.Study of the structural and mechanical performance of underwater shield-bored high speed railway tunnels and the boring and docking technologies［D］.Beijing:School of Civil Engineering，Beijing Jiaotong University，2011.(in Chinese))