諧振接地系統單相接地故障暫態特性分析

姚麗寶 黃世遠

（1.福州省電力有限公司寧德電業局，福建 寧德 352100；2.福建省電力有限公司檢修分公司，福州 350013）

諧振接地系統具有較高的供電可靠性，但長時間帶單相接地故障運行將影響電力系統的安全運行[1]，因此在發生接地故障后，需盡快準確的選出故障線路。

利用單相接地故障時產生的暫態信號來判斷故障線路是近年來故障選線研究的主要方向。根據所利用的暫態特征，主要可分為兩類：①利用暫態過程的時域特征[2-3]，此為傳統的選線方法；②利用故障時零序網絡中線路的相頻特性，這是研究的新方向[4-6]。但目前上述兩種方法均存在明顯缺點：①傳統基于簡化模型分析所得的暫態時域特征結論不盡完善，特別對接地點過渡電阻的影響考慮不足，因此對大電阻接地故障的選線準確率不高；②現有基于線路相頻特性所得的暫態零序容性電流的分布規律適應度有限，特別是對越發廣泛使用的纜-線混聯傳輸線適應度較小，導致該方法的準確性和靈敏度大為降低[7-8]。

針對上述問題，本文在時域上研究了故障電壓初相角、過渡電阻對暫態特征的影響，在頻域上通過分析各種結構線路輸入阻抗的相頻特性，確定了暫態零序容性電流在不同類型傳輸線路上的分布規律。

1 暫態接地電流時域特征

1.1 諧振接地系統等值回路

暫態接地電流通常認為由故障相電壓驟降引起的放電電流和非故障相電壓驟升引起的充電電流兩部分組成。本文僅研究充電電流的暫態過程，系統簡化模型如圖1所示[9]。

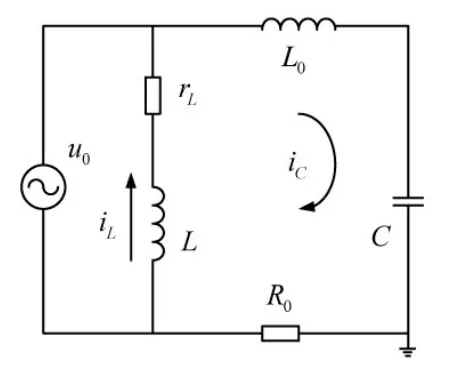
圖1 諧振接地電網單相接地等值回路

圖中，u0為零序電源電壓；rL，L分別為消弧線圈的有功損耗電阻和電感；L0為零序回路的等值電感；R0為零序回路中的等值電阻；C為電網三相對地電容總和。

由圖 1，根據疊加原理，暫態接地電流id可認為由暫態電容電流iC和暫態電感電流iL疊加而成。計算iC時，通常認為自由振蕩頻率較高的iC對電感具有阻隔作用，且由于L＞＞L0，從而忽略L，即忽略iL，直接由L0、C、R0組成的串聯回路和作用于其上的零序正弦電源電壓u0，經時域分析求得iC。iL可由非線性電路的基本理論導出。則由iC和iL疊加而成的id表達式為

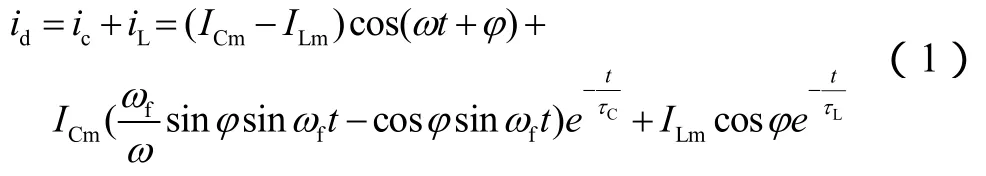
式（1）又可分解為兩部分：①由第一項單獨構成的接地電流穩態分量；②由第二項電容電流的暫態自由振蕩分量與第三項電感電流的暫態直流分量之和構成的接地電流暫態分量。

分析暫態分量表達式可知，振蕩分量與直流分量的幅值均決定于故障電壓初相角，且二者成逆向分布關系。振蕩分量的最大值出現在初相角為 90°的奇數倍時，此時直流分量約等于 0；直流分量的最大值則出現在初相角為180°的偶數倍時，此時振蕩分量可忽略不計。

1.2 仿真模型

利用Matlab的PSB搭建諧振接地系統的分布參數模型如圖2所示，其中線路1和線路3分別為由10km電纜和 10km架空線路組成電纜-架空混聯線路及架空-電纜混聯線路，線路2為長10km的架空線路，線路4為長10km的電纜線路。圖中架空線路正、零序參數為：R1=0.17Ω/km，C1=0.00969μF/km，L1=1.21 mH/km，R0=0.23Ω/km，C0=0.008 μF/km，L0=5.478 mH/km；電纜線路正、零序參數為：R1=0.27Ω/kmC1=0.339μF/km，L1=0.255mH/km，R0=2.7Ω/km，C0=0.028μF/km，L0=1.019 mH/km；消弧線圈補償度為5%。

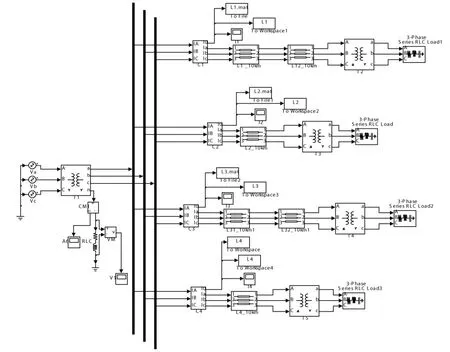
圖2 諧振接地系統仿真模型

1.3 故障初相角對暫態特征的影響

因受篇幅限制，本文僅列舉相電壓過峰值和過零點兩個典型時刻來分析故障初相角對暫態電流的影響。設在A相電壓相角分別為270°（相電壓過峰值）和0°（相電壓過零點）時，線路4在距母線1km處發生單相接地故障，接地電阻1Ω，仿真得各饋線的暫態電流分別如圖3和圖4所示。

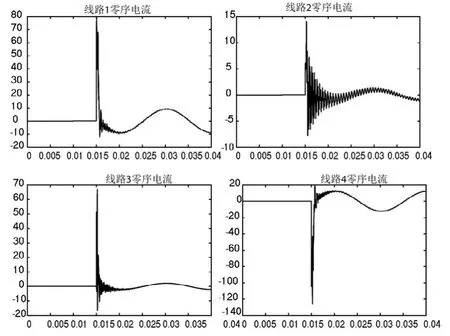
圖3 初相角270°時各饋線暫態電流

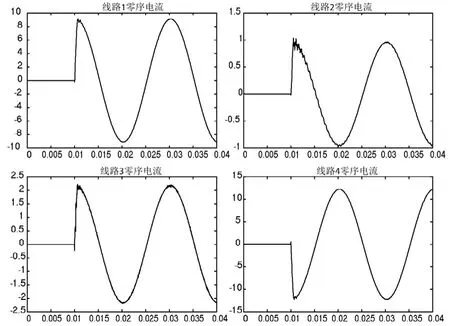
圖4 初相角0°時各饋線暫態電流

經分析不同故障初相角的仿真結果，可得以下結論：①故障發生在相電壓過峰值時，所有饋線暫態電流均明顯存在一個含有大量高頻振蕩分量的暫態過程，當故障發生在相電壓過零點時，饋線暫態電流中基本不存在振蕩分量，以直流分量為主，此結果與前文分析一致；②架空線路的振蕩頻率較含電纜饋線的小得多，說明線路結構對暫態電流頻譜具有影響；③故障線路暫態電流幅值最大，健全線路中含有電纜的線路幅值大于純架空線路的幅值，說明線路參數對暫態電流幅值具有影響；④故障線路暫態電流與健全線路極性相反。

1.4 故障點過渡電阻對暫態特征的影響

過渡電阻對暫態電流的影響包括直接影響與間接影響。直接影響是指過渡電阻直接影響暫態分量幅值，過渡電阻越大，暫態電流幅值越小。間接影響是指過渡電阻通過暫態電流幅值間接影響電容充電速度，幅值越大，充電越快，電容電流的振蕩頻率越高，反之亦然。由此分析可知，受過渡電阻對電容電流振蕩頻率的影響，1.1節中所求得的暫態接地電流必然僅適用于一定大小的過渡電阻。根據電力系統分析可知，式（1）僅適用于以下兩種情況：

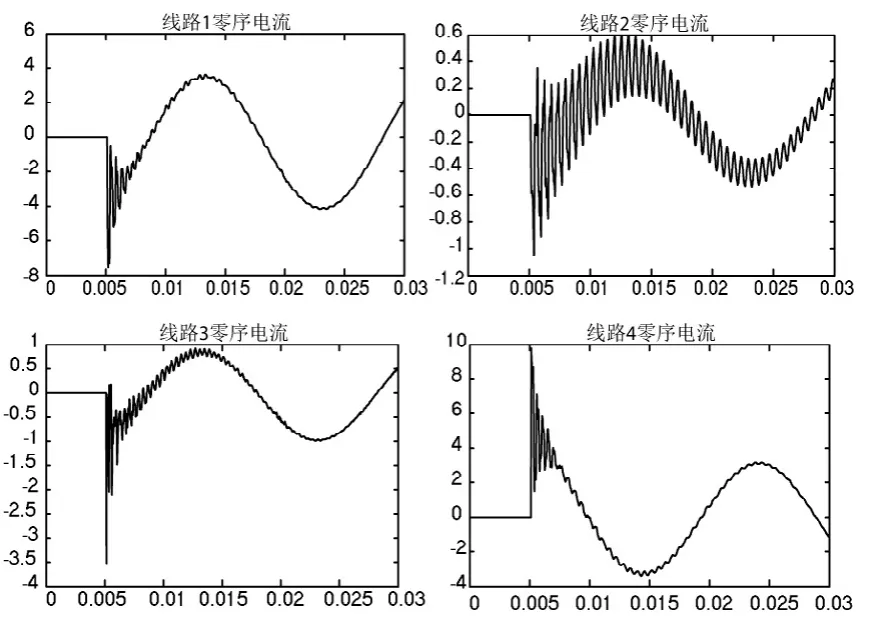
圖5 過渡電阻較大時線路暫態電流

而對于更大的過渡電阻，因暫態電容電流振蕩頻率過低（最低可至工頻），將不可忽略L對C的作用。為求此過渡電阻的大小，可忽略L0及rL，由L與C組成的并聯回路求得，過渡電阻需滿足。此時，系統處于欠阻尼狀態，其暫態電流如圖6所示，呈周期性振蕩衰減。

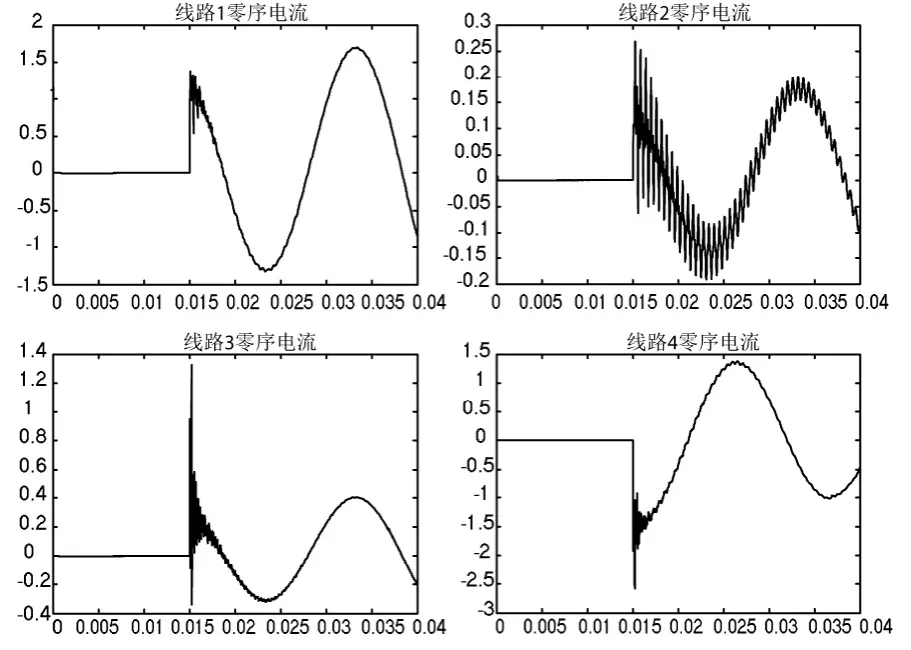
圖6 大過渡電阻時線路暫態電流

多次仿真結果還表明，R0越大，暫態電壓首半波、幅值與第二個半波幅值比值將越小，如圖7所示。

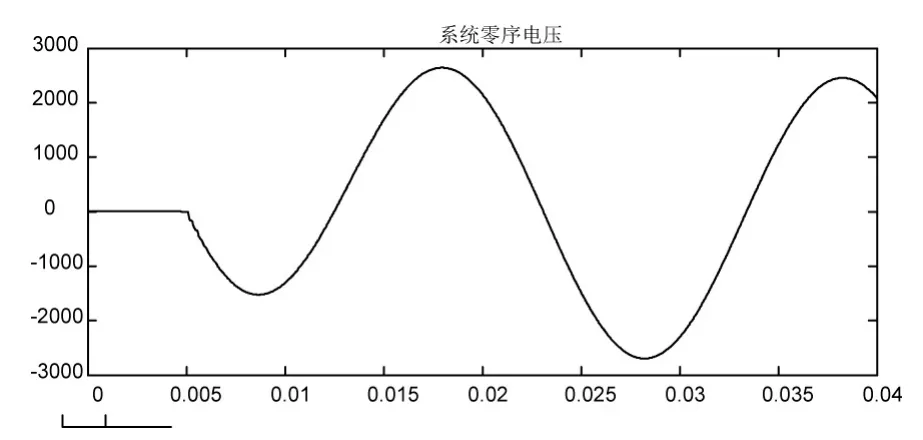
圖7 系統暫態電壓

2 暫態接地電流頻率特征

2.1 基于線路分布參數的故障模量模型

從時域分析暫態電流實現了對暫態過程的宏觀了解，但從上述分析過程可發現時域分析方法存在以下兩個明顯缺點：

1）電感對系統的影響收頻率作用明顯，若對頻率大小考慮不足，一概通過忽略電感來簡化系統模型，可能因此得出與實際情況相反的結論。

2）僅片面的從時域分析暫態特征，完全拋棄了對系統頻率特征差異的分析，這對于結構復雜的系統，極可能因不正確使用故障信息而導致選線錯誤。

因此上述從時域分析暫態電流所得的結論顯然存有不足，很有必要繼續從頻域分析暫態接地電流在不同頻段上的特性，以進一步完善暫態電流特征。為此，線路自身電感及消弧線圈電感均必須予以考慮。利用卡倫包爾變換，依據故障分析原理和疊加原理，可得從故障點看到的基于線路分布參數模型的系統故障零序網絡等效圖[10]，如圖8所示。

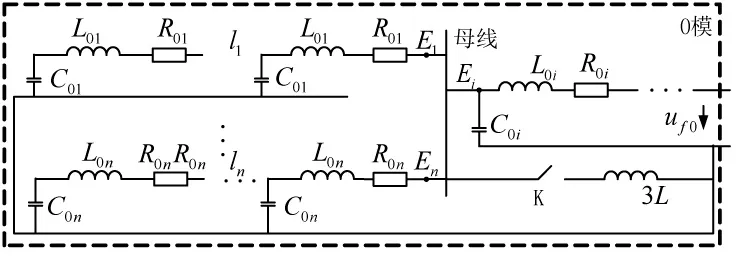
圖8 基于線路分布參數的故障零序網絡等效圖

此圖是從頻域分析暫態接地電流特征的基礎，圖中，L0k、C0k、R0k、Ek、lk分別為饋線k的單位長度零序電感、單位長度零序電容、單位長度電阻、檢測點及饋線長度；L為消弧線圈自身等效電感；開關K控制中性點接地方式，對于諧振接地系統K為閉合。

2.2 諧振零序網暫態相頻特性分析

隨著城市建設的快速發展，目前城市配電網已不再僅由架空線路構成，而是同時采用了架空線路、電纜線路以及電纜與架空線相混聯的復雜線路，以下針對這些應用中常見的線路類型進行分析。

1）健全線路暫態相頻特性分析

為獲得在檢測點處檢測到的線路等效阻抗，可依據二端口網絡原理，將圖8中任意一條健全線路k末端看做開路，再利用傳輸方程求得。

對于單一均勻傳輸線路，包括架空線路和電纜線路，其等效阻抗表達式為

忽略較小的線路電阻，將ω=2πf帶入式（2）可得阻抗Z0ck關于f的函數：

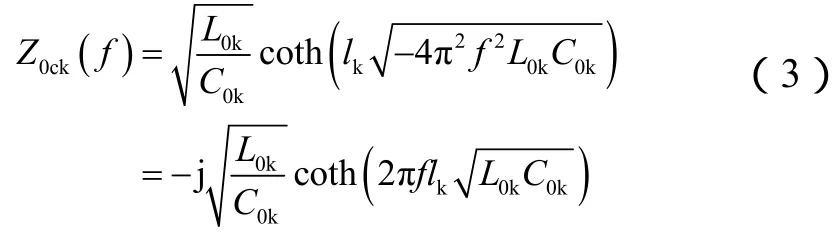
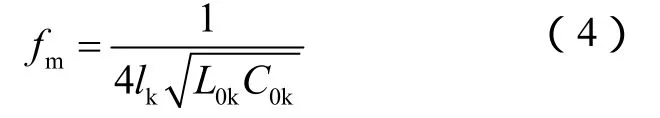
由式（4）可知，對于單位長度零序電感及零序電容大小相等的線路，線路越長，fm越小；對于長度相同的線路，單位長度零序電感或零序電容越大，fm越小。

對于母線出線處為電纜，后轉架空線路的電纜-架空混聯線路，等效阻抗表達式為

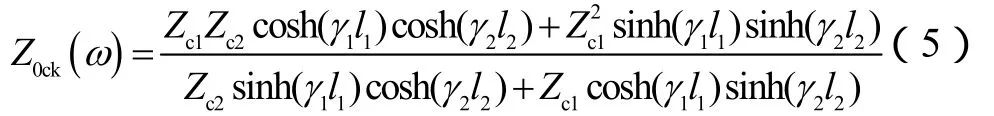
式中，各參數意義與式（2）相同，下標1，2分別表示電纜線路和架空線路。

對于母線出線處為架空線路，后轉電纜的架空-電纜混聯線路，線路輸入阻抗表達式為

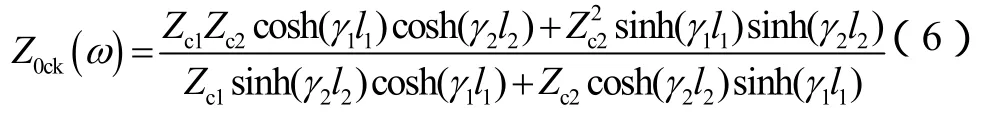
對于其他結構線路，可同理推得其等效阻抗表達式，這里不再繼續給出。但顯然線路結構越復雜，其相應等效阻抗表達式也越復雜。根據所得等效阻抗，研究中利用Matalb獲得相應的相頻特性圖。

由式（2）、式（5）及式（6）可知，影響輸入阻抗的因素包括線路參數及線路結構。據此，分以下三類進行仿真：①長度分別為10km和20km的架空線路，相頻特性如圖9（a）所示；②長度均為10km的架空線路和電纜線路，相頻特性如圖9（b）所示；③均由10km電纜和10km架空線路組成的電纜-架空混聯線路和架空-電纜混聯線路，相頻特性分別如圖 9（c）、9（d）所示。

圖9 不同條件下線路的相頻特性

針對首次發生串聯諧振的頻率fm及相頻特性波形兩個主要特征，通過比較圖9的各子圖可得如下結論：①20km架空線路具有的fm明顯小于10km架空線路的fm，電纜線路因單位長度零序電容遠大于架空線路，故10km電纜線路的fm遠小于同長度架空線路的fm，這些與前文分析一致；②架空線路的容性頻段阻抗角等于-π/2，感性頻段阻抗角等于π/2，波形總體為一方波，而電纜線路的相頻特性總體類似正弦波；③電纜-架空混聯線路的fm決定于該線路中電纜段線路的fm，與架空段線路無關，波形較不規則；④架空-電纜混聯線路的fm較同長度電纜-架空混聯線路的fm小的多，波形更顯不規則。

2）故障線路暫態相頻特性分析

與健全線路檢測點檢測的是本線路等效阻抗不同，故障線路檢測點檢測的是故障線路背后所有線路并聯的總等效阻抗。對于諧振接地系統，故障線路檢測到的導納應為所有健全線路及消弧線圈的并聯導納（采用導納表示可使表達式簡潔），即

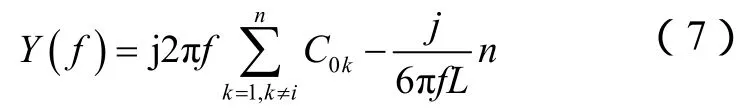
式中，C0k表示健全線路等效集中電容，n表示健全線路的總條數。因此該導納的相頻特性勢必較任意一條健全線路都更為復雜，具體表現為：①串聯諧振由任意一條健全線路的串聯諧振引起，故其fm等于所有健全線路fm的最小值fmmin；②并聯諧振由所有健全線路之間的并聯諧振引起。

輪流以線路1、2、3、4為故障線路，得到的故障線路檢測點的背后阻抗相頻特性如圖10順序所示。

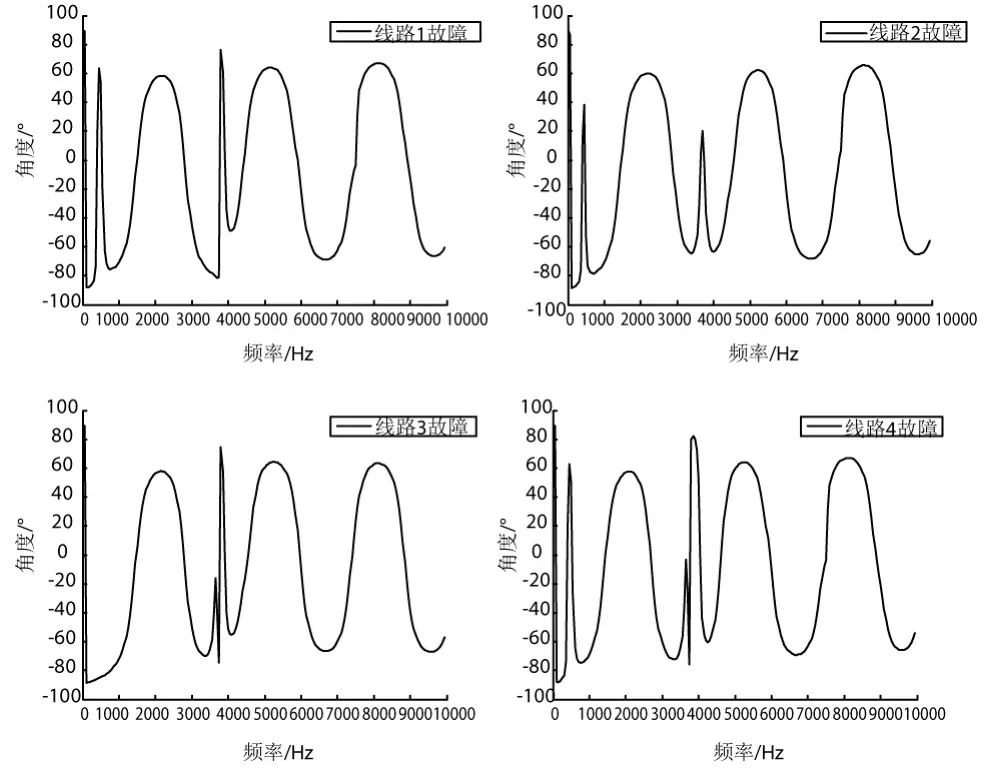
圖10 故障線路檢測點相頻特性

將圖9與圖10結合比較可知：①消弧線圈僅對故障線路的相頻特性產生影響，且僅使首個容性頻段之前產生一次并聯諧振。設首次并聯諧振頻率為fB，最大值fBmax在具有最大等效集中電容C0k的線路發生故障時取得；②從首個并聯諧振之后的相頻特性波形完全決定于健全線路的串并聯諧振，總體復雜無規則，這與前文分析一致。

2.3 選定頻段（SFB）的確定

由上述分析，諧振接地系統的 SFB可定義為fBmax到fmmin的頻段。在SFB范圍內，所有線路（包括健全線路和故障線路）檢測點檢測到的等效阻抗均為容性阻抗，從而可簡化圖8為圖11所示。

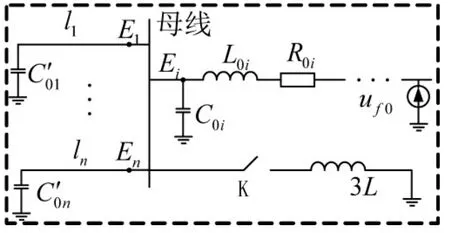
圖11 故障時SFB內零序網絡等效圖

根據圖11，在SFB內所有健全線路暫態電流極性相同，而與故障線路極性相反，且故障線路的暫態零序電流幅值等于所有健全線路幅值之和，這與從時域分析所得結果一致。但在SFB之外，因健全線路之間存在諧振的可能，即健全線路阻抗不再恒定同為容性或感性，此時前面的分析結論不再恒定成立，這也再次驗證了分析暫態頻域特征的必要性。

結合穩態分析結論，顯然暫態零序電流在 SFB內的特性與穩態一致。因此在且僅在SFB內，從暫態過程到穩態過程，即在故障后的所有時間內，均有以下結論：對于諧振接地系統，當線路發生單相接地故障時，故障線路和健全線路暫態零序電流極性相反，故障線路的零序電流幅值等于所有健全線路幅值之和；當母線發生單相接地故障時，所有線路零序電流都由母線流向線路，極性相同。

3 結論

根據電力系統故障分析的一般知識，本文首先從時域上分析了諧振接地系統在發生單相接地故障后，故障初相角和接地電阻對系統零序暫態特征的影響。由于利用簡化模型從時域分析暫態過程所得結論不盡完善，甚至有一定錯誤，故又從頻域上詳細分析了現有配電網中廣泛采用的各種結構線路等效阻抗的相頻特性，確定了諧振接地系統的 SFB。最后，通過綜合故障后的暫態電流時、頻特征和穩態時域特征，進一步確定了在不同類型傳輸線路上暫態零序容性電流的分布規律。經Matlab仿真實驗，驗證了所得結論的正確性，為下一步更準確利用暫態分量進行故障選線打下了堅實理論基礎。

[1] 要煥年,曹梅月.電力系統諧振接地[M].北京：中國電力出版社,2000.

[2] 操豐梅,蘇沛浦.小波變換在配電自動化接地故障檢測中的應用研究[J].電力系統自動化, 1999,23(13)：33-36.

[3] 龔林春,黃摯雄.基于小波包的小電流接地故障選線仿真研究[J].計算機科學與工程, 2008,30(3)：103-105.

[4] 王偉,焦彥軍.暫態信號特征分量在配網小電流接地選線中的應用[J].電網技術,2008, 34(4)：96-100.

[5] 薛永端,馮祖仁,徐丙垠.中性點非直接接地電網單相接地故障暫態特征分析[J].西安交通大學學報, 2004,38(2)：195-199.

[6] 王耀南,霍百林,王輝,等.基于小波包的小電流接地系統故障選線的新判據[J].中國電機工程學報,2004,24(6)：54-58.

[7] 潘露,呂艷萍,于芳,等.基于相頻特性與多頻帶分析的小電流接地系統故障選線[J].電力系統自動化, 2007,31(4)：76-79.

[8] 張偉剛,張保會.中性點非直接接地系統零序網絡的相頻特性[J].電力自動化設備,2010,30(3)：71-75.

[9] 張艷霞,王清亮.應用故障暫態特性實現配電網故障選線的新方法[J].電力系統自動化,2009,33(16)：76-80.

[10] 張新慧.基于Prony算法的小電流接地故障暫態選線技術[D].山東：山東大學,2008.