基于FLAC3D的邊坡爆破臨界振速的確定

萬保安，黎 杉，熊茂東

(1．江西公路開發總公司，江西 南昌 330038;2．江西贛粵高速公路股份有限公司，江西 南昌 330025)

基于FLAC3D的邊坡爆破臨界振速的確定

萬保安1，黎 杉2，熊茂東1

(1．江西公路開發總公司，江西 南昌 330038;2．江西贛粵高速公路股份有限公司，江西 南昌 330025)

邊坡爆破臨界振速的確定是巖土爆破開挖過程中的關鍵問題。結合對永平銅礦高陡邊坡穩定性的分析，介紹了基于FLAC3D的邊坡爆破臨界振速的確定方法。首先建立邊坡靜力分析模型，使模型達到自重作用下的平衡狀態，其次通過施加不同爆破振動峰值速度的爆破過程來確定邊坡破壞的爆破臨界振速，之后可以得到最大段裝藥量與爆心至邊坡坡腳距離之間的關系式。介紹了邊坡破壞的判別準則和應用FLAC3D求解的流程。

邊坡 爆破振動 FLAC3D臨界振速

巖土邊坡爆破振動臨界振速的確定，是巖土爆破開挖過程中的關鍵問題［1-3］。其影響因素很多，如巖石物理力學性質、地質構造、邊坡高度、邊坡坡角等。爆破震動可引起邊坡不同程度的破壞，如出現大滑移、部分巖石滾落、巖層出現裂隙、巖層彈性變形不能完全恢復、產生巖層損傷積累等。鑒于上述原因，確定邊坡臨界振速比確定各種建筑物的臨界振速要復雜得多［4-7］。正因如此，《爆破安全規程》及大量參考文獻，僅對各種建筑、水工涵洞和礦山巷道等構造物的臨界振速作出了規定，而對邊坡只粗略規定了臨界振速的參考值，其范圍太大，在實際操作中使用不便。

本文結合永平銅礦高陡邊坡穩定性分析工程實例，采用FLAC3D軟件對邊坡爆破臨界振速進行研究，探討了一種確定臨界振速的方法。

1 基于FLAC3D 的邊坡爆破臨界振速的分析方法

FLAC3D不僅可以進行靜力分析、滲流分析，還可以進行非線性動力反應分析，爆破振動作用下邊坡的穩定性可以采用FLAC3D進行研究。為確定邊坡所能承受的最大爆破振動速度，可采用如下思路進行研究:

1)建立邊坡 FLAC3D模型，先采用靜力模型，使模型達到自重作用下的平衡狀態，即邊坡處在爆破前的自然狀態。

2)分別將不同峰值的爆破振動速度時程曲線施加在邊坡模型上，分析模型的動態響應;通過不斷試算，確定恰使邊坡發生破壞的振動速度曲線，該曲線對應的振動速度峰值即為邊坡所能承受的最大爆破振動速度。

1.1 爆破振動速度的確定

實際的爆破振動波形很復雜，但對于地質體，影響最大的一般是其中的某個波段。在很多研究中，若沒有實際監測爆破振動波形，為便于計算，通常將爆破振動波形簡化為簡諧波來處理。簡諧波質點振動速度方程為

式中:V為t時刻質點的振動速度，m/s;Vmax為振動速度峰值;f為振動頻率，Hz;t為時間，s。

關于速度時程曲線方程式(1)中f的選值問題，大量的現場爆破振動監測結果表明，爆破振動的頻率范圍很廣，一般為20～200 Hz，爆破振動作用時間一般為0.17～0.42 s。

1.2 邊坡破壞的判別準則

巖土體受到破壞之后強度會發生變化，而包括FLAC3D在內的多數模擬軟件很難對這一過程進行模擬，因為當巖土體開始滑動的時候軟件并未對其強度進行及時更新，這就導致了在模擬過程中很難出現非常明顯的垮塌現象。因此，對于任何軟件模擬方法，均應對模擬結果進行判斷。下面介紹兩種比較適合于判斷邊坡是否破壞的方法。

1)監測并觀察運算過程的最大不平衡力

在數值分析中，收斂標準直接控制計算求解的時間以及精度。所謂收斂標準，是指數值計算求解過程終止的判定條件。在FLAC3D中，必須由用戶自己確定收斂標準。最大不平衡力和最大不平衡力率是FLAC3D的兩種收斂標準。最大不平衡力，是指每一個計算循環(或稱計算時步)中，外力通過網絡節點傳遞分配到體系各節點時，所有節點的外力與內力之差中的最大值;最大不平衡力率，是指最大不平衡力與典型內力的比率(典型內力是指計算模型所有網絡點力的平均值)。由于FLAC3D采用動態求解方式，整個系統一直處于某種運動狀態，不可能達到真正意義上的平衡，而只能認為當不平衡程度降低到某個值時(默認情況下為最大不平衡力率減小到10－5)系統達到了平衡狀態。因此，監測系統的最大不平衡力可以發現系統是否破壞，因為如果材料已經破壞則模型將發生塑性流動，在塑性流動停止之前系統將可能無法達到平衡。

2)觀察剪切應變增量云圖或分析位移情況

最大不平衡力能夠收斂并不說明巖土體未發生破壞，因為巖土體破壞后也有可能重新達到平衡。所以，還應觀察模型的變形情況才能確定巖土體是否破壞。

邊坡破壞一般是巖土體發生剪切破壞引起的，巖土體屬于塑性材料，無法承受太大的應變。FLAC3D中的剪切應變增量云圖是表征材料發生塑性變形情況的等值線圖。因此，在用FLAC3D進行工程分析時，通常通過觀察巖土體中剪切應變增量云圖來判斷巖土體是否破壞。一般來說，如果剪切應變增量云圖的等值線貫穿整個巖土體，在巖土體表面形成一個封閉的圈，則可以判定巖土體發生破壞了。

此外，還可以通過分析模型中各部位的位移情況來判斷模型是否發生破壞。通過分析位移情況，可直觀地發現模型的變形情況，若變形量較大(如達到米級)，超出了一般巖土體的承受范圍，說明巖土體已經發生破壞;若變形量較小(如毫米級)，則說明巖土體未發生破壞。

總的來說，如果出現以下三種情況之一，則可判定巖土體發生破壞:①系統的最大不平衡力無法收斂;②剪切應變增量云圖貫穿整個巖土體;③變形量達到一般巖土體難以承受的范圍。如果最大不平衡力收斂且出現以下兩種情況之一，則說明巖土體穩定:①剪切應變增量云圖未貫穿整個巖土體;②變形量在一般巖土體可承受范圍之內。

2 FLAC3D 的一般求解流程

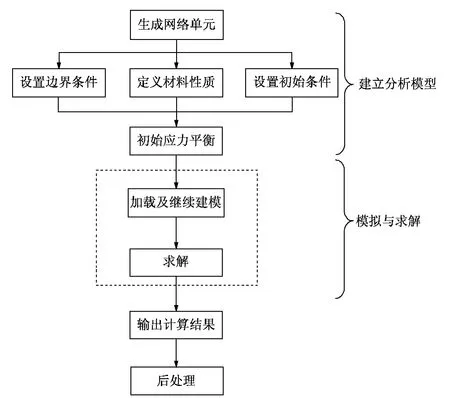
圖1 FLAC3D的一般求解流程

圖1顯示了FLAC3D的一般求解流程。圖1中的生成網絡單元是指對研究對象建立模型，將研究對象采用若干差分網格來代替，網格單元僅在節點處存在聯系;之后對網絡單元設置邊界條件和初始條件，并對材料性質賦予參數;然后進行初次求解達到初始應力平衡，至此，模型的初始狀態已經形成。

加載與繼續建模是指，對達到初始平衡狀態的模型施加外力或開挖，打破模型的初始平衡狀態，之后給出收斂要求，再次求解使模型達到平衡或破壞，輸出計算結果。

最后一步是后處理，是指將運算結果以某種方式把需要的信息顯示出來，可以是圖片或表格等形式，用以分析模型達到再次平衡時的狀態。

3 算例分析

3.1 模型的建立

江西省永平銅礦大規模生產性開采至今已有20多年，以露天開采為主，采場周邊形成了許多規模不等的露采邊坡，坡高由幾十米到400 m不等。隨著開采深度繼續加深，露天邊坡高度將不斷增加，坡度也逐漸增大，給礦山生產安全帶來隱患。為此，研究生產過程特別是爆破開挖過程中邊坡的穩定性成為該礦山進一步安全生產及可持續發展的關鍵。

該礦山北坑西坡進行爆破作業過程中穩定性分析的核心問題是確定爆破振動作用下的臨界振速，該邊坡主要巖體的物理力學參數如表1所示。

由于邊坡剖面與邊坡走向接近垂直，且在走向方向上剖面變化不大，這樣二維模型與三維模型的計算結果相差不大，卻可顯著節省計算時間，因此采用二維模型計算。圖2為北坑西坡典型剖面。

表1 模型材料力學參數

圖2 北坑西坡剖面示意

3.2 計算結果分析

據現場調查，目前采礦爆破地點距北坑西坡坡腳約50 m，最大段裝藥量約為1 000 kg，實踐證明該爆破方案未使邊坡發生失穩。依據薩道夫斯基公式，并通過回歸分析取參數K、α分別為104.315和1.834 3(K和a分別為與爆破點至保護對象間的地形、地質條件有關的系數和衰減指數)，則地面振動速度V的計算公式為

式中:Q為最大段裝藥量，kg;R為爆心至觀測點的距離，m。

將R=50 m，Q=1 000 kg代入式(2)得爆破在邊坡坡腳產生的振動速度V=5.448 cm/s，由此可說明北坑西坡能承受5.448 cm/s的振動速度。

下面首先對模型施加振速峰值為7.0 cm/s的爆破荷載，然后逐漸增加，直至邊坡發生破壞為止。通過觀察模型塑性變形單元的分布情況來判斷邊坡是否發生破壞。單元發生塑性變形，說明該單元的承載能力達到了極限，如果塑性變形的單元貫穿了邊坡，可判斷邊坡發生了破壞。

圖3為不同振速峰值的爆破過程爆破振動結束時邊坡塑性變形單元分布情況。

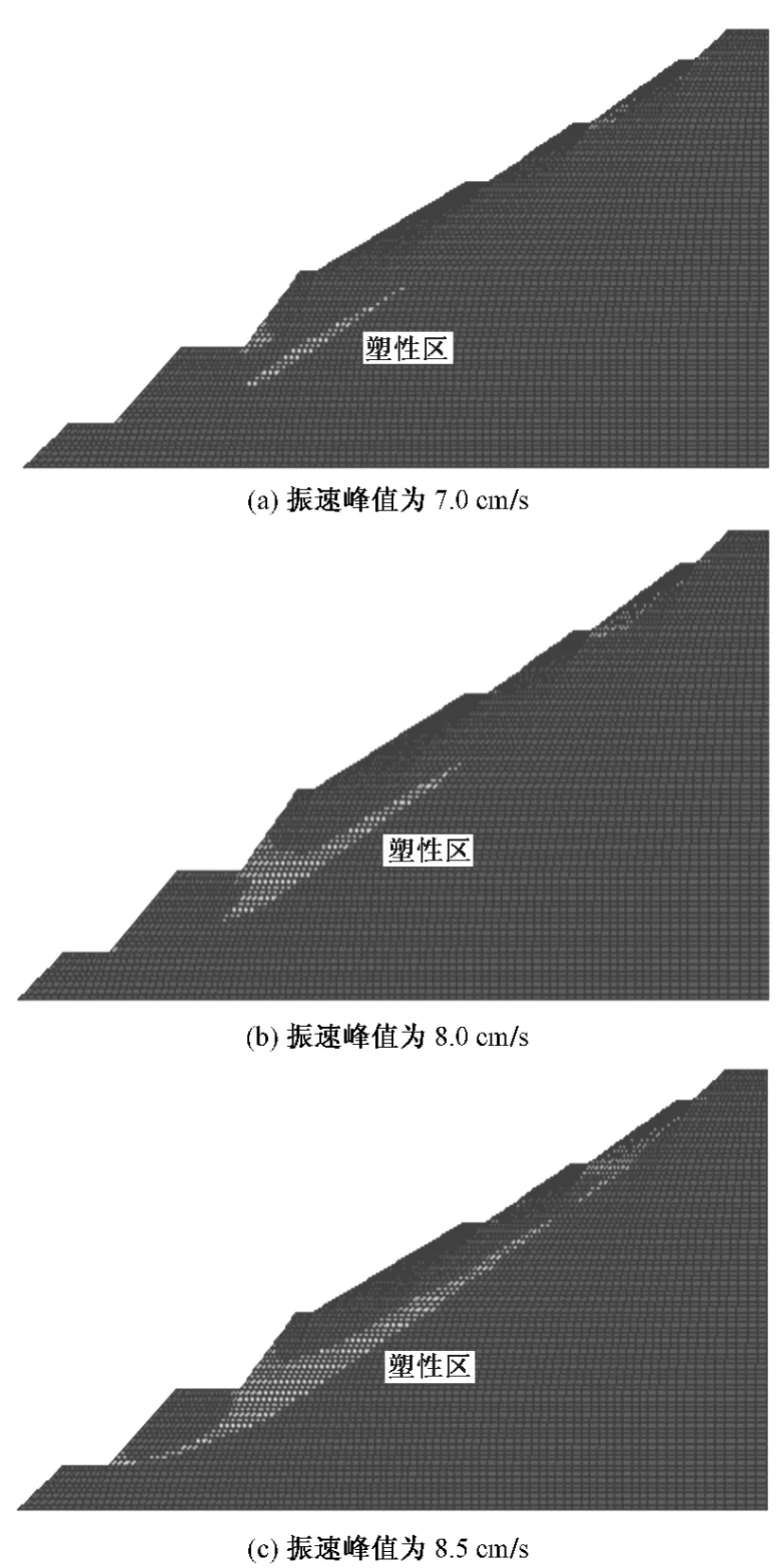
圖3 不同振速峰值的爆破過程邊坡塑性變形分布

由圖3(a)可以看出，在振速峰值為7.0 cm/s爆破荷載作用下，邊坡坡腳及一些平臺出現了小范圍的塑性變形單元，可見爆破荷載對邊坡產生了影響。由于塑性變形單元未貫穿邊坡，可認為邊坡穩定。從圖3(b)可以看出，在振速峰值為8.0 cm/s的爆破荷載作用下，邊坡的塑性變形單元明顯多于7.0 cm/s時，但塑性變形單元仍未貫穿邊坡，可認為邊坡穩定。從圖3(c)中可以看出，在振速峰值為8.5 cm/s的爆破荷載作用下，北坑西坡的塑性變形單元已經貫穿了上面的幾級臺階，塑性變形單元也貫穿了整個邊坡，說明邊坡將發生大范圍滑坡。

從以上的模擬結果可知，北坑西坡所能承受的最大爆破振動速度為8.0 cm/s，將 V=8.0 cm/s代入式(2)中，可得到最大段裝藥量Q與爆心至觀測點的距離R之間的關系式為

從上式可以看出，因為 Q與R的立方成正比，隨著距離R的增大，允許的最大段裝藥量迅速增加。當在距離邊坡較近的地方進行爆破時，須非常謹慎地控制最大段裝藥量，避免爆破振動引發滑坡。式(3)為礦山爆破作業最大段裝藥量的確定提供了理論依據。

4 結語

應用FLAC3D軟件對邊坡爆破振動作用下的穩定性進行了分析，通過建立邊坡的數值模型，并逐漸加大爆破振動速度，可以直觀地得到爆破過程邊坡塑性變形單元發展情況，從而合理確定邊坡保持穩定的臨界振速。該方法不僅可以指導邊坡安全爆破施工，還可以為類似邊坡工程臨界振速的預測和施工設計提供參考。

［1］宋小林，張繼春，郭學彬，等．順傾邊坡巖體爆破的振動特性數值研究［J］．鐵道建筑，2010(2):87-90．

［2］許名標，彭德紅．巖質高陡邊坡爆破降振技術研究［J］．鐵道建筑，2011(8):93-96．

［3］朱傳云，盧文波，董振華．巖質邊坡爆破振動安全判據綜述［J］．爆破，1997，14(2):13-17．

［4］曹孝君，吳青山，張繼春，等．順層巖質邊坡的爆破振動控制標準試驗研究［J］．巖石力學與工程學報，2003，22(11):1924-1928．

［5］劉世波．多臺階開挖中的爆破振動傳播規律研究［J］．鐵道建筑，2008(1):68-70．

［6］汪旭光，于亞倫．關于爆破震動安全判據的幾個問題［J］．工程爆破，2001，7(2):88-92．

［7］唐春海，于亞倫，王建宙，等．爆破地震動安全判據的初步探討［J］．有色金屬，2001，53(1):1-3．

Determination of critical vibration velocity of blasting for slopes based on FLAC3D

WAN Baoan1，LI Shan2，XIONG Maodong1

(1．Jiangxi Highway Development Corporation，Nanchang Jiangxi 330038，China;2．Jiangxi Ganyue Expressway Co．，Ltd．，Nanchang Jiangxi 330025，China)

The determination of the critical blast-inducing vibration velocity is crucial in soil slope excavation．This paper uses the stability analysis of the high steep rock slope of Yong Ping copper mine as an example and introduces the determining method of the critical blast-induce vibration velocity using FLAC3Dsoftware．First，static analysis model was built for the object of study to remain in its natural state with no influence from external force;and then，the critical blast-inducing vibration velocity of the slope was determined by imposing blasting operations with different peak velocity．By this means，the relation between maximum explosive load and the distance of explosion center to the toe of slope can be concluded by a single formula．At the same time，the paper reviews the principle for the determination of slope destruction and the application of FLAC3D．

Slope;Blasting-inducing vibration;FLAC3D;Critical vibration velocity

U416.1+13;U416.1+4

A

10．3969/j．issn．1003-1995．2013．08．35

1003-1995(2013)08-0115-04

2012-12-07;

2013-05-26

江西省交通運輸廳科技項目基金資助(2010C00013)

萬保安(1955— )，男，江西新建人，高級工程師。

(責任審編 李付軍)