大體積非桿系混凝土承載板的配筋

何 學，汪基偉，冷 飛

(河海大學土木與交通學院，江蘇南京 210098)

大體積非桿系混凝土承載板的配筋

何 學，汪基偉，冷 飛

(河海大學土木與交通學院，江蘇南京 210098)

以實際工程為背景，采用模擬施工法和疊合梁法計算大體積非桿系混凝土承載板的應力，討論兩種方法所得結果的區別及不同彈性模量隨時間變化的計算公式對計算結果的影響，再按應力圖形法進行承載力配筋，并采用鋼筋混凝土有限元法進行裂縫驗算。計算結果表明:采用模擬施工法計算時，不同彈性模量隨時間變化的計算公式對最大主拉應力與關鍵截面的主拉應力影響不大;雖然模擬施工法得到的拉應力最大值大于疊合梁法，但兩者所得應力分布規律相同，關鍵截面的主拉應力和承載力所需的配筋量相近;按應力圖形法所配鋼筋能滿足裂縫寬度的要求;大體積非桿系混凝土承載板的配筋設計可采用簡單的疊合梁法計算應力分布，按應力圖形法配筋，除特別重要的結構外一般可不用鋼筋混凝土有限元法進行裂縫寬度計算。

大體積混凝土;結構配筋;模擬施工法;疊合梁法;應力圖形法;有限元法

工程中處理水電站壩基內深槽的一般方法是先用混凝土替換，再澆筑壩體。某工程為加快施工進度，提出采用鋼筋混凝土承載板洞挖全置換混凝土方法處理深槽，具體為:①橫跨深槽設置厚13.5 m的鋼筋混凝土承載板;②壩前設置防滲體;③澆筑上部壩體混凝土，同時挖除承載板下方深槽內的砂卵礫石;④深槽內回填混凝土并灌漿。在這種處理方式中，承載板承擔了上部兩個壩段的自重，并將其傳遞至深槽兩邊的基巖之上，是關鍵承重結構，因此承載板的配筋設計是置換混凝土法成功的關鍵。

承載板屬于大體積非桿系混凝土結構，一般按應力圖形法進行配筋，對重要的非桿系混凝土結構還宜采用鋼筋混凝土有限元法進行裂縫控制驗算［1-2］。

按應力圖形配筋首先要合理確定承載板的最不利應力分布，因此本文采用模擬施工法和疊合梁法對承載板的應力分布進行計算，討論兩種方法及不同彈性模量隨時間變化計算公式對計算結果的影響;再采用鋼筋混凝土有限元法模擬施工過程，計算裂縫開展，進行裂縫寬度驗算。

1 計算模型與計算條件

選取最危險剖面，按平面應變問題進行計算，剖面尺寸見圖1。承載板分5層澆筑，其高度分別為6.0 m、1.5 m、2.0 m、3.0 m 和 3.0 m;壩體碾壓混凝土以每層高度3.0 m澆筑，有14層，即承載板加壩體共分19層澆筑。線性與非線性計算均模擬分層澆筑的施工過程。

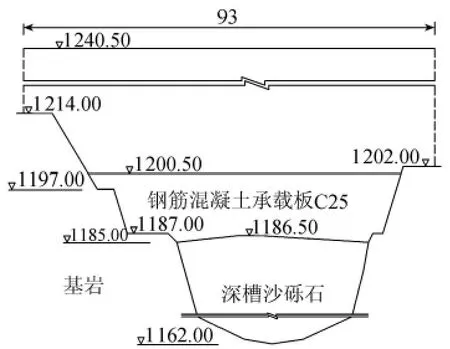
圖1 計算剖面示意圖(單位:m)

模型取1 m寬，基礎深取承載板底高程向下86 m，基礎寬取從承載板底部向左右各延長120m。基礎的底部、左右側均布置法向鏈桿支座。

計算采用汪基偉等［3］自行研制的鋼筋混凝土有限元軟件HohaiRCFE-P，該程序已應用于較多工程的配筋研究［4-6］。承載板、壩體與基巖均采用4～8結點等參單元，本文需計算裂縫寬度，承載板的網格，特別是裂縫出現區域劃分得很密，考慮到裂縫垂直方向出現，因此水平方向單元尺寸不大于65 mm，在垂直方向大一些，不大于100 mm。

非線性計算時，考慮鋼筋的作用，主要受力鋼筋采用分離式單元模型計算，其中鋼筋采用桿單元，黏結單元采用雙彈簧單元;其他鋼筋采用帶黏結滑移埋置式單元［7-8］。承載板采用等效單軸應變本構模型［9-11］模擬;鋼筋采用帶硬化段的彈塑性模型模擬;鋼筋與混凝土黏結滑移曲線采用Houde公式［12］計算，并筋鋼筋的表面積乘0.5的系數;基巖、壩體混凝土、砂礫石仍按線性材料計算。

壩體混凝土28 d彈性模量28 GPa，泊松比0.16，密度2500 kg/m3;基巖彈性模量14 GPa，泊松比0.26，在承載板澆筑前基巖沉降已完成，故不考慮自重;砂礫石彈性模量80 MPa，泊松比0.30，不考慮自重。

承載板混凝土按 C25計算，28 d彈性模量Ec(28)=28 GPa。混凝土彈性模量隨時間的變化分別采用式(1)和式(2)計算，以分析彈性模量隨時間變化采用不同公式計算對應力的影響，其中式(1)為SL191—2008《水工混凝土結構設計規范》中的公式;式(2)為經驗公式。

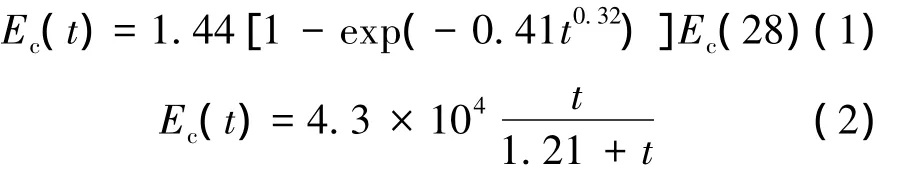
式中:t為齡期。

非線性計算時材料強度取標準值，承載板混凝土28 d抗拉強度標準值ftk(28)=1.78 MPa，28d抗壓強度標準值fck(28)=16.70 MPa;鋼筋采用HRB335，彈性模量Es=200 GPa。

2 線性計算

2.1 模擬施工法計算

模擬施工法是模擬分層澆筑的施工過程，并考慮彈性模量隨時間變化的計算方法。每澆筑層間隙時間為7 d，計算步長取1 d，彈性模量取該時段的平均值。計算起點為第1澆筑層澆筑的第1天，計算終點為最后澆筑層澆筑后第28天。

第1層混凝土澆筑后，承載板底部(A區)、上部肩部(B區、C區)受拉，而且上部肩部的主拉應力大于底部(圖2(a))。第2層混凝土澆筑后，承載板底部的主拉應力已大于上部肩部的主拉應力(圖2(b))。此后，各層混凝土澆筑后，主拉應力最大值均出現于承載板底部，見圖2(c)。

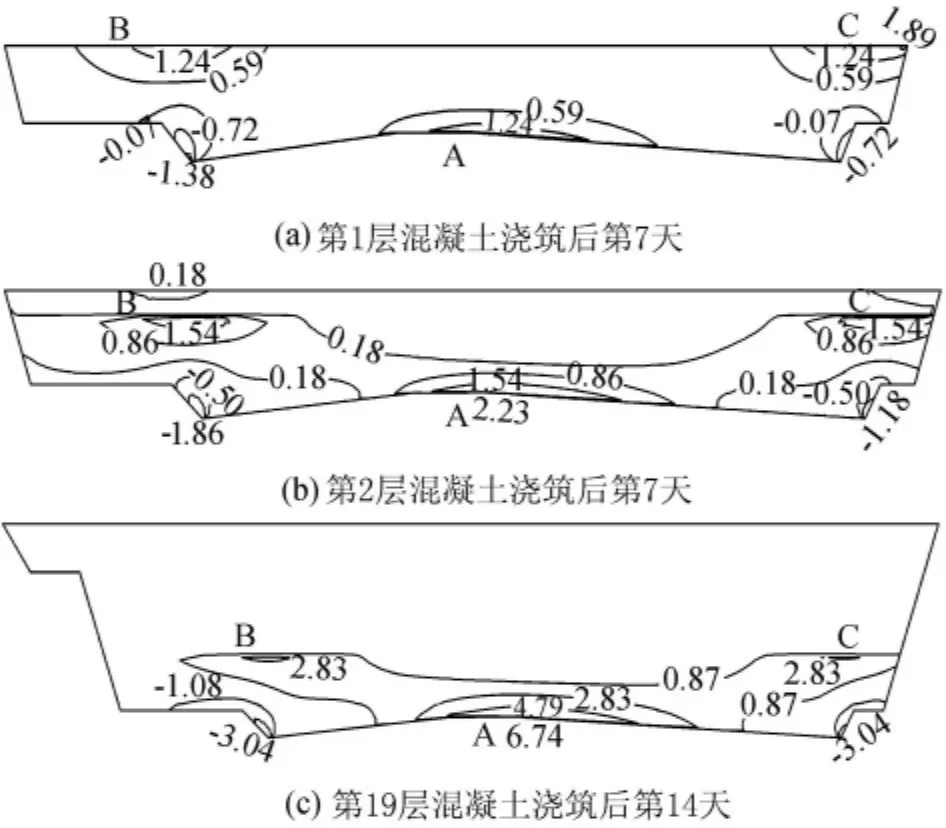
圖2 模擬施工法得到的承載板主拉應力等值線(單位:MPa)

2.2 疊合梁法計算

疊合梁法仍模擬分層澆筑的施工過程，但不考慮彈性模量隨時間的變化。假定承載板的第1層自重全部由巖基均勻承擔，不在本層內產生應力。計算開始于第2層澆筑后，這時第1層的彈性模量取為28 d的彈性模量，第2層的自重按作用于第1層頂面的分布荷載施加;第3層澆筑后，第2層的彈性模量取為28 d的彈性模量，第3層的自重按作用于第2層頂面的分布荷載施加;其他各層，以此類推。

第1層澆筑、將第2層自重作為分布荷載施加后，承載板底部、上部肩部受拉，而且上部肩部的主拉應力大于底部。第2層澆筑、將第3層自重作為分布荷載施加后，承載板底部的主拉應力已大于上部肩部的主拉應力，這時應力最大值出現位置和模擬施工法相同。圖3為第1層澆筑、將第2層自重作為分布荷載施加后，第18層澆筑、將第19層自重作為分布荷載施加后的承載板主拉應力等值線圖。

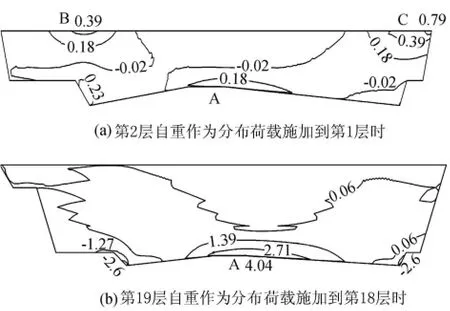
圖3 疊合梁法得到的承載板主拉應力等值線(單位:MPa)

2.3 線性計算結果分析

表1給出了分別按模擬施工法和疊合梁法得出的各層澆筑完后承載板的最大主拉應力及其發生的位置和主拉應力在配筋方向投影形成的合力，其中，模擬施工1的彈性模量采用式(1)計算，模擬施工2的彈性模量采用式(2)計算。由表1可以看出:

a.第3層澆筑完成后，按上述3種方法進行線性計算得出的承載板最大主拉應力出現的位置相同，均出現于底拱中心附近，數值隨著澆筑高程的增加而增大，即主拉應力分布規律與變化規律相同。

b.當澆筑相同的混凝土層時，模擬施工1與模擬施工2得出的最大主拉應力相差都在10%以內，關鍵截面主拉應力在配筋方向投影形成的合力相差也都在10%以內。當混凝土澆筑完成后，主拉應力值更為接近，分別為6.74 MPa與6.27 MPa，相差7%;合力也更為接近，分別為10543.6kN與10396.6 kN，相差1.4%。因此，彈性模量計算公式不同對承載板的應力影響不大。

c.疊合梁法得到的主拉應力最大值明顯小于模擬施工法，疊合梁法與模擬施工1相比，在澆筑承載板各層時，兩者的主拉應力值相差60%左右;而在澆筑壩體時，兩者的主拉應力值相差也在40%左右;在壩體澆筑完成后，兩者相差42%。但關鍵截面主拉應力在配筋方向投影形成的合力大小較為接近，在澆筑承載板各層時，相差20%左右;而在澆筑壩體時，相差6%左右;在壩體澆筑完成后，只相差4.2%。疊合梁法計算簡便，用于配筋的合力計算和模擬施工法相差很小，可以代替模擬施工法。

2.4 按應力圖形法配筋

由表1所列主拉應力在配筋方向的合力值，按DL/T 5057—2009《水工混凝土結構設計規范》規定的應力圖形法進行配筋計算，其中強度設計值fy=300 MPa。按模擬施工1所得的配筋用量為48325 mm2/m，模擬施工2為47 648 mm2/m，疊合梁法為46305mm2/m。按3種方法計算得出的配筋面積相差不大，按疊合梁法得出的鋼筋用量選配筋如圖4所示。

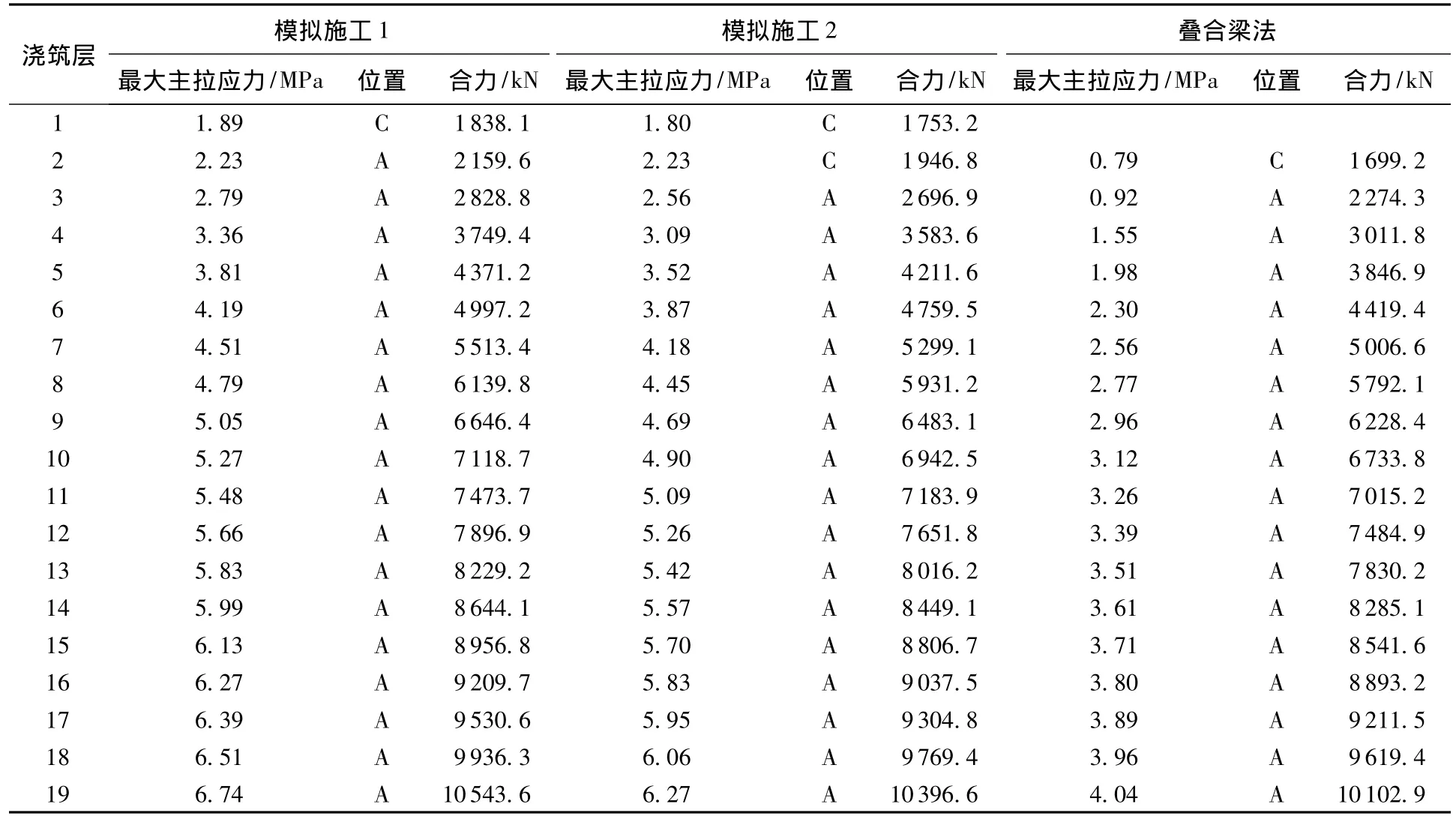
表1 線性計算結果

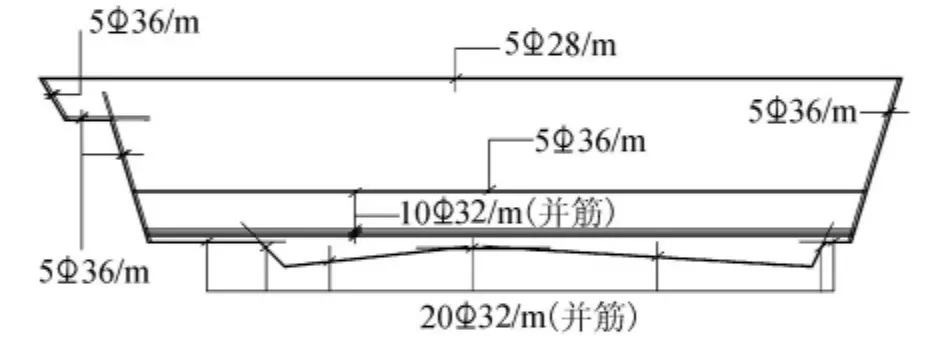
圖4 配筋示意圖

3 非線性計算

在第1層混凝土澆筑后，承載板底部主要裂縫為2條，最大裂縫寬度表面為0.09mm，內部為0.17mm;承載板上部左肩部也出現垂直裂縫，由于該處沒有配筋，裂縫開展很深;承載板右側沿基巖出現滑移。第2層混凝土澆筑后，在原底部裂縫的左側又出現1條主要裂縫，承載板底部主要裂縫從2條增加到3條，最大裂縫寬度表面0.11mm、內部0.21mm。第7層混凝土澆筑后，在原底部裂縫的右側又出現1條主要裂縫，承載板底部主要裂縫增加到4條，最大裂縫寬度表面0.20mm、內部0.44mm。最后一層混凝土澆筑后，主要裂縫為5條，最大裂縫寬度表面0.34mm、內部0.54mm。圖5給出了施工過程中的承載板裂縫分布。

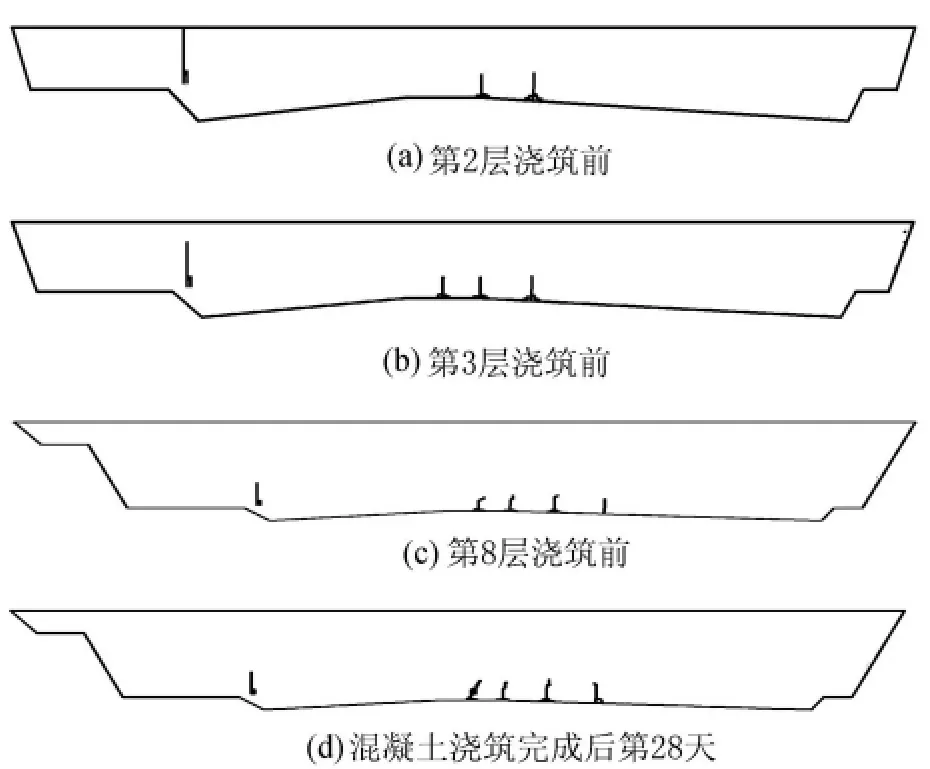
圖5 承載板的裂縫分布

表2給出了各層澆筑后、下一層澆筑前的裂縫寬度。從表2可以看出，裂縫寬度呈表面小、內部大的形態，內部最大裂縫寬度出現于承載板底面第1排與第2排鋼筋之間，最大裂縫寬度表面為0.34mm、內部為0.54 mm。最大表面寬度略大于0.30 mm限值，可以認為配筋滿足裂縫寬度的要求。

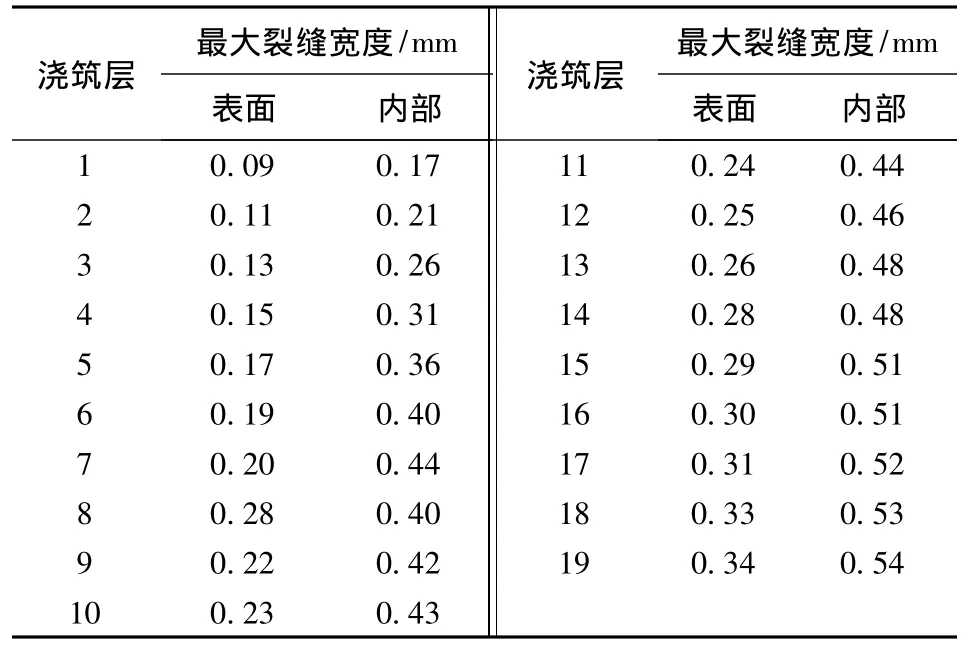
表2 各層澆筑后的最大裂縫寬度

4 結論

a.按不同彈性模量公式計算得出的承載板主拉應力值及其在配筋方向投影形成的合力大小都較接近，即彈性模量計算公式不同對承載板應力影響不大。

b.雖然疊合梁法得到的承載板主拉應力最大值比模擬施工法小許多，但兩者所得應力分布規律相同，且關鍵截面主拉應力在配筋方向投影形成的合力大小和承載力所需的配筋量都比較相近。

c.按應力圖形法所配鋼筋能滿足裂縫寬度的要求。

d.此類承載板的配筋設計可采用簡單的疊合梁法計算應力分布，按應力圖形法配筋，除特別重要的結構外一般可不用鋼筋混凝土有限元法進行裂縫寬度計算。

［1］SL 191—2008 水工混凝土結構設計規范［S］.

［2］DL/T 5057—2009 水工混凝土結構設計規范［S］.

［3］汪基偉，張雄文.水工鋼筋混凝土結構有限元設計計算原則［J］.水利水電科技進展，2005，25(5):44-47.(WANG Jiwei，ZHANG Xiongwen.Calculation principle for finite element design of hydraulic reinforced concrete structures［J］.Advances in Science and Technology of Water Resources，2005，25(5):44-47.(in Chinese))

［4］吳勝興，汪基偉，朱虹.三峽升船機塔柱筒體結構溫度配筋研究［J］.河海大學學報:自然科學版，1998，26(2):21-25.(WU Shengxing，WANG Jiwei，ZHU Hong.A study on temperature reinforcement of tube-structure of ship lift for the Three Gorges Project［J］.Journal of Hohai University:Natural Sciences，1998，26(2):21-25.(in Chinese))

［5］汪基偉，鈕新強，楊本新.三峽升船機上閘首結構配筋方案研究［J］.人民長江，2001，32(11):8-10.(WANG Jiwei，NIU Xinqiang，YANG Benxin.Study on structural reinforcement for the upper lock head of ship lift for the Three Gorges Project［J］.Yangtze River，2001，32(11):8-10.(in Chinese))

［6］汪基偉.船閘裂縫成因及加固措施的研究［J］.水利水電技術，2001，32(9):5-9.(WANG Jiwei.Study on cause of cracking and improvement measures of a lock［J］.Water Resources and Hydropower Engineering，2001，32(9):5-9.(in Chinese))

［7］汪基偉，張雄文，林新志.考慮黏結滑移的平面組合式單元模型研究與應用［J］.工程力學，2008，25(1):97-102.(WANG Jiwei，ZHANG Xiongwen，LIN Xinzhi.Research and applications of a plane embedded combined element model considering bond and slip［J］.Engineering Mechanics，2008，25(1):97-102.(in Chinese))

［8］龍渝川，張楚漢，周元德.鋼筋混凝土嵌入式滑移模型［J］.工程力學，2007，24(增刊 1):41-45.(LONG Yuchuan，ZHANG Chuhan，ZHOU Yuande.Embedded slip model for analyzing reinforced concrete structures［J］.Engineering Mechanics，2007，24(Sup1):41-45.(in Chinese))

［9］DARWIN D，PECKNOLD D A.Non-linear bi-axial stressstrain law for concrete［J］.Journal of the Engineering Mechanics Division，1977，103(2):229-241.

［10］汪基偉，朱虹，王紅.平面應變狀態混凝土等效單軸應變本構模型研究［J］.河海大學學報:自然科學版，2002，30(1):6-10.(WANG Jiwei，ZHU Hong，WANG Hong.Equivalent uniaxial constitutive model of concrete in plane strain［J］.Journal of Hohai University:Natural Sciences，2002，30(1):6-10.(in Chinese))

［11］汪基偉，陳玉泉.平面應變混凝土強度變形試驗與等效單軸應變本構模型［J］.東南大學學報:自然科學版，2005，35(5):775-779.(WANG Jiwei，CHEN Yuquan.Strength-deformation test and equivalent uniaxial constitutive model of concrete in plane strain［J］.Journal of Southeast University:Nature Sciences，2005，35(5):775-779.(in Chinese))

［12］康清梁.鋼筋混凝土有限元分析［M］.北京:中國水利水電出版社，1996.

Reinforcement of massive non-member concrete bearing plate

HE Xue，WANG Jiwei，LENG Fei(College of Civil and Transportation Engineering，Hohai University，Nanjing210098，China)

The stress of massive non-member concrete bearing plate is calculated based on a practical project by means of the simulating construction method and the composite beam method.The differences between their calculated results as well as the influences of different formulae for the variation of elastic modulus with time are discussed.The reinforcement of bearing capacity is determined by use of the stress graphic method，and the crack width is verified by means of the reinforced concrete finite element method(RCFEM).The results show that the maximum tensile principal stress and tensile force of the key cross section are not obviously affected by the formula for the variation of elastic modulus with time by applying the simulating construction method.Although the maximum tensile principal stress yielded by the simulating construction method is larger than that by the composite beam method，the distribution laws of their calculated stresses are the same，and their tensile forces and reinforcements of bearing capacity of the key cross section are very close.The reinforcement according to the stress graphic method can meet the requirements of crack width control.The distribution of stress of massive non-member concrete bearing plate can be calculated by means of the simple composite beam method，and the reinforcement can be determined by use of the stress graphic method.It is not necessary to employ RCFEM to verify the crack width for similar structures except special ones.

massive concrete;structural reinforcement;simulating construction method;composite beam method;stress graphic method;finite element method

TU375.2

A

1006-7647(2013)01-0058-04

10.3880/j.issn.1006-7647.2013.01.013

何學(1987—)，男，江蘇昆山人，碩士研究生，主要從事混凝土結構研究。E-mail:hxhexue@163.com

2012-04-22 編輯:熊水斌)