諧分量法在機組動平衡中的應用

李煜涵， 曹封勇， 吳勝波， 趙繼云

（貴州華電畢節熱電有限公司，貴州畢節 551713）

0 引言

不平衡是引起機組振動的主要故障之一，現場動平衡是消除其振動的主要手段[1]，主要方法包括影響系數法和模態平衡法，諧分量法在模態平衡法中以簡單實用著稱。影響系數法在剛性轉子動平衡中相對在柔性轉子中應用更為準確，當利用影響系數法進行柔性轉子動平衡時，遇到了很多問題，此方法本身并沒有給平衡技術增加新的內容，在某些柔性轉子的現場動平衡中諧分量法相對更為經濟有效。

1 不平衡振動機理

通過兩端剛性支承的Jeffcott為研究對象來了解不平衡引起振動的機理[2],如圖1所示。

轉子靜態撓曲線為A1-c-A2。如果圓盤質心c和轉軸中心o’不重合，如圖2所示，質心c的加速度在坐標軸上的投影為：

式中xc—質心c的X坐標，mm；

yc—質心c的Y坐標，mm；

e—圓盤的偏心距，mm；

Ω—轉子旋轉角速度，rad/s。

軸心運動微分方程：

式中 ωn—軸系臨界角速度，rad/s；

x，y—軸中心坐標。

該方程解即為不平衡響應：

式中 z—軸中心不平衡響應，mm。

2 諧分量法原理

如圖3所示，一階振型下，轉子兩端振動同相；二階振型下，轉子兩端振動反相。將平衡轉速下的振動按圖4分解為同相和反相分量。

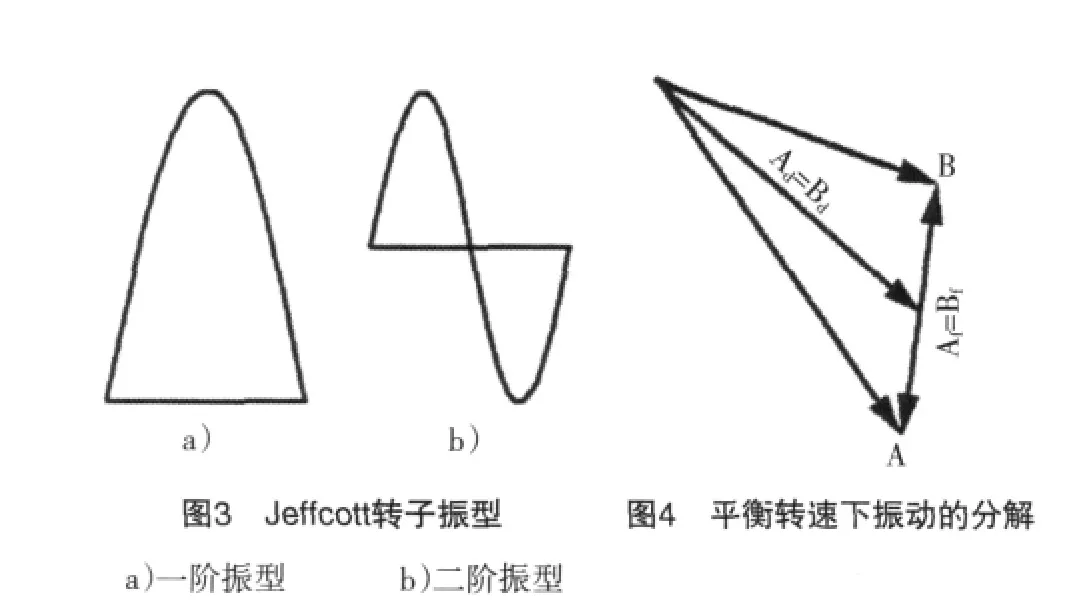
諧分量法的出發點是，若在轉子兩端施行對稱加重，即可消除一階型式的振動。若施加反對稱配重，則可消除二階振動。

實際應用諧分量法進行動平衡時，在平衡轉速下將原始振動分解為同相分量和反相分量；在選定的兩平衡面上同時試加重；測量加重后的振動并將其分解為同相和反相分量；計算對稱和反對稱加重的影響系數；最后利用該影響系數計算應加重。

3 工程案例

3.1 某燃氣輪機動平衡

某電廠的燃氣輪機由西門子公司制造，軸系由透平、壓氣機、發電機轉子及4個徑向支撐軸承組成，軸系如圖5所示。

現場在發電機兩端#1、#2瓦水平、垂直方向安裝速度傳感器，將速度傳感器接入ZXP-F8振動數據采集儀，再通過網線將采集儀接入電腦，顯示振動數據及各圖形。

形聲字是現代漢字的主體，其中形符的表義功能，有助于留學生理解漢字的含義；聲符的示音功能，利于留學生了解讀音。對外漢語教師運用形聲字的這些優勢進行教學，不僅可以減輕學生們的負擔，而且能夠增強他們的信心，激發他們學習漢字的熱情。

分析所采集的振動數據，發電機兩端瓦振水平方向相對垂直方向較大，且絕大部分為工頻分量，振動穩定，按照故障的性質來分該類型振動屬于穩定的普通強迫振動。尋找引起發電機兩端瓦振較大的故障原因時，首先應從轉子激振力和發電機兩端支撐動剛度兩大方面著手。軸承座支撐動剛度的大小取決于軸承座靜剛度、部件間的連接剛度和支撐系統是否存在共振三個方面。一般情況下由于實際中改變軸承座本身靜剛度或部件自振頻率工作量較大，所以不論是由軸承座靜剛度不足，還是由支撐系統存在共振引起的振動，首先應從降低激振力入手。這里如果再能排除連接剛度的故障，即可排除支撐故障引起的振動。現場手持便捷式速度傳感器測量發電機兩端軸承座連接部件間的差別振動，結果差別振動很小，都在合格范圍內，因此可判斷該機振動是由激振力較大引起的。又由于振動絕大部分為工頻分量且穩定，則可判斷該發電機轉子存在一定的質量不平衡，決定對發電機進行動平衡。

該燃機第一次啟動升速到3000rpm時，#1瓦振為28μm∠344°，#2瓦振為46μm∠137°，將兩端瓦振按諧分量進行分解，反相分量占絕大部分，同相分量很小，于是決定在發電機兩端進行反對稱加重，#1瓦處加重320g∠120°，#2瓦處加重320g∠300°。

啟動定速后，#2瓦振降低10μm，但仍較大，且#1瓦振較加重前有所增大，故對配重進行了調整，拆除上次加重，在#1瓦處加重200g∠135°，#2瓦處加重200g∠315°。此次啟動后兩瓦振較原始振動振幅未變化，相位有所變化，效果不理想，于是取下之前加重，綜合前兩次加重數據，最后決定在#1瓦加重370g∠77°，#2瓦加重370g∠257°，此次加重后#1、#2瓦振皆為10μm左右，達到廠家要求，至此燃機動平衡工作結束。歷次加重及#1、#2瓦振動見表1。

3.2 某發電機動平衡

3.2.1 例1

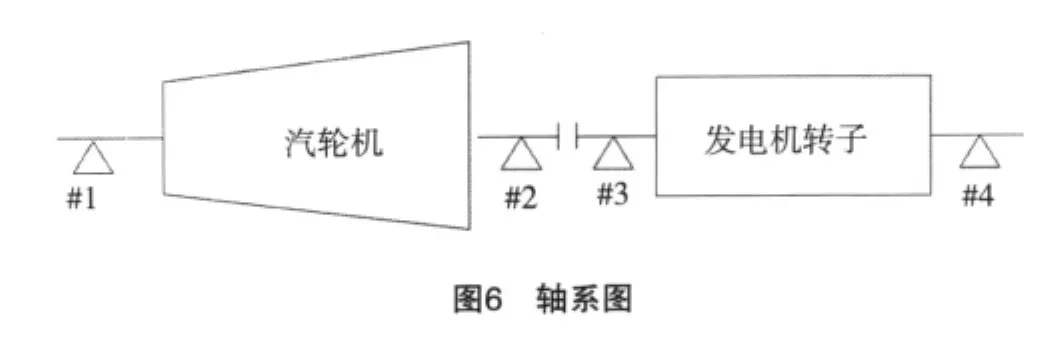
某廠#2號汽輪機由長江動力集團武漢汽輪發電機廠生產，型號為CC60-8.83/4.3/1.5，發電機型號為QF-60-2，該機軸系由汽輪機轉子、發電機轉子以及4個徑向軸承組成，軸系如圖6所示。

該機帶55MW負荷時，3Y振動為83/80μm∠241°，4Y為84/82μm∠99°，振動穩定。停機過程中當轉速達2955r/min時 ，3Y為60/59μm ∠251°，4Y為 58/51μm∠127°，且振動以穩定的基頻分量為主。各瓦振很小，可以排除因支撐系統動剛度不足引起的機組振動；空轉時穩定的基頻振動在排除支撐剛度不足故障后認為是由發電機轉子的本身不平衡引起的，另外考慮到該機帶負荷相對空轉時振動增大25μm左右，因此在動平衡過程中應同時考慮空轉和帶負荷時的振動情況。

表1 某燃氣輪機動平衡過程數據

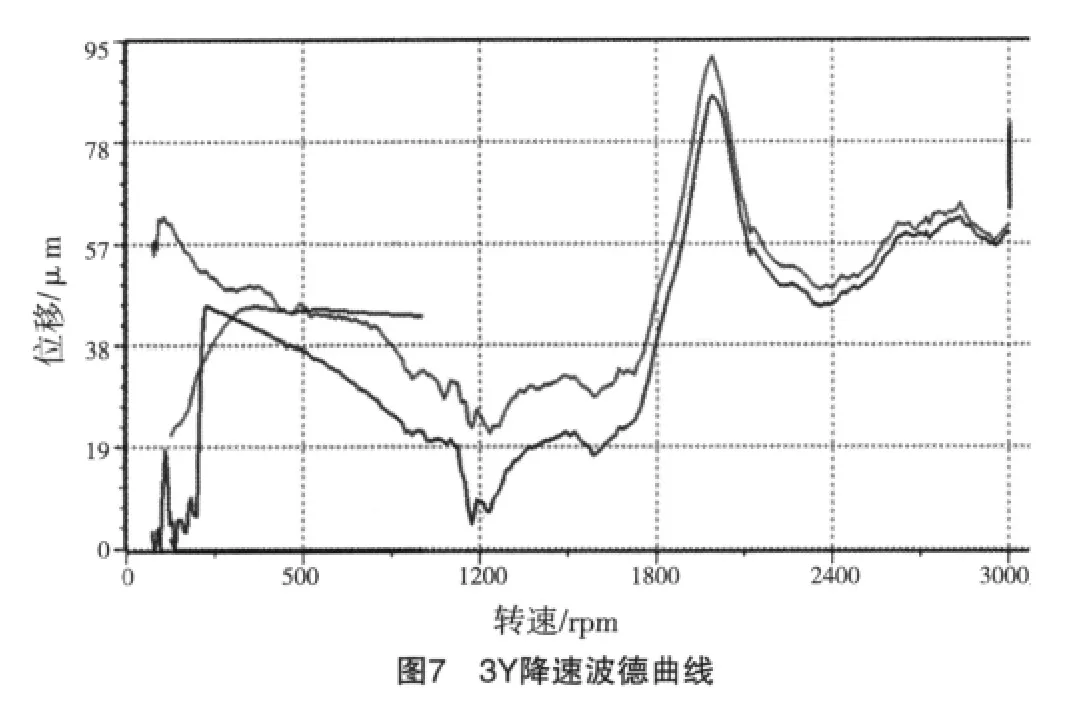
當降速到280r/min時，發現3Y處軸頸晃度46μm∠324°，如圖7所示，4Y處晃度23μm∠210°，為使發電機轉子動平衡時能一次加準，軸振應扣除原始晃度并同時兼顧帶負荷時的振動，即將空轉下振動扣除原始晃度后，再加上帶負荷時相對空轉時的振動熱變量的一半[1]，計算動平衡的原始振動3Y應為75μm∠211°，4Y為75μm∠91°，諧分量分解后同相分量為37μm∠150/150°，反相分量為65μm∠240/60°。

根據該機轉子結構、振動特性，首次在發電機兩端反對稱加重，在#3、#4瓦端分別加重200g∠300°、200g∠120°。啟動帶10MW負荷時3Y振動42/29μm∠156°，4Y為42/39μm∠245°，當帶44MW負荷時3Y、4Y振動40μm左右，其他瓦中軸振最大的4X為55μm，振動達廠家要求，該發電機動平衡通過諧分量法一次加準即將振動降到較小幅值。

3.2.2 例2

南京某廠#1號汽輪發電機組型號與3.2.1中的機組相同。該發電機原始振動較大，絕大部分為基頻分量，且振動很穩定，該振動性質為穩定的普通強迫振動。由于瓦振很小，軸承座連接部件間的差別振動都在合理范圍內，排除軸承座支撐動剛度不足的故障，則該機振動大是由于轉子激振力較大導致的。由于占振動絕大部件的工頻分量很穩定，判斷發電機存在不平衡，決定對其進行動平衡。

由于發電機兩端反相振動分量占主要部分，故首先應平衡掉反相分量，在發電機兩端實施反對稱加重，#3端加300g∠95°，#4端加300g∠275°，平衡過程見表2。

試加重后的效果較為明顯，幅值和相位都有變化，因此利用此次加重數據計算得到的影響系數應較為準確，由于試加重后4Y方向振動還是比較大，且發電機兩端軸振仍以反相分量為主，于是保留上次加重，然后按照上述影響系數計算所需配重大小和加重方向，在#3瓦側加200g∠0°，#4瓦側加200g∠180°。定速后該發電機兩端軸振在45μm左右，振動達優良水平，至此動平衡工作結束。

表2 某廠＃1發電機動平衡過程數據

4 結語

經過上述三個工程案例，驗證了諧分量法在解決不平衡引起的振動中的有效性。因此，諧分量法在現場動平衡中有較好的應用價值。但是，由于諧分量法是建立在柔性轉子動力特性分析的基礎上，如果要使用得當，則需要對轉子動力特性有一個比較深入的認識。

：

[1]陸頌元.汽輪發電機組振動[M].北京：中國電力出版社，2000.

[2]范雷雷.轉子系統不平衡相應傳遞規律研究[D].南京：東南大學，2005.