礦柱失穩的突變分析

韓 穎，楊志龍

（河南理工大學能源科學與工程學院，河南 焦作454000）

沖擊地壓和煤與瓦斯突出是煤礦開采中的兩種嚴重的動力災害，在煤礦開采尤其是條帶開采中礦柱起著十分重要的作用。近年來隨著煤礦開采的深度越來越大，礦柱沖擊地壓現象在煤炭開采中時有發生，所以研究影響礦柱沖擊地壓的因素及其機理顯得尤為重要。目前，許多學者對礦（煤）柱沖擊地壓進行了多方面的研究，谷惠棠、胡慧明[1]結合材料力學理論，建立了巖梁－礦柱的尖點突變模型，提出了系統發生失穩破壞的條件及發生失穩破壞時系統釋放的能量。李忠華、潘一山[2]提出應用煤層塑性軟化理論和材料失穩的動力判別準則，對煤柱沖擊地壓進行的解析分析方法。王玉山[3]提出了壓機－巖樣加載系統模型來描述礦柱的失穩行為，并用之解釋了國內典型礦山中礦柱系統失穩破壞的災變特征。王存文、姜福興等[4]通過建立下保護層中殘留孤島煤柱的結構力學模型，用力學原理分析了殘留煤柱及被保護層煤體中的應力狀態，得到煤柱誘發沖擊地壓的機理。李江騰、曹平[5]應用能量原理及突變理論推導礦柱失穩的臨界載荷及臨界應力，提出礦柱發生失穩的屈曲模型。作為一種嘗試，本文在前人的基礎上將礦柱近似為由彈性元件和塑性軟化元件串聯組成，建立了頂板－礦柱圍巖系統的力學模型；應用突變理論建立了頂板－礦柱圍巖系統失穩發生沖擊地壓的尖點突變模型。

1 力學模型

沖擊地壓是煤巖體快速、突然釋放彈性能的現象。在礦井開采過程中常常留有礦柱，有的是三面采空的“孤島”礦柱，有的是上下工作面間留設的區段保護礦柱.這些礦柱由于采后殘余支承壓力的影響，通常在煤巖體中造成很大的應力集中[6]。礦柱是地下巖體中唯一承受單軸壓縮荷載的構件[7]。頂底板－礦柱圍巖系統和巖樣的單軸壓縮非常相似，巖樣在進行單軸壓縮時，隨著荷載的增大首先出現線彈性變形，當巖樣應力達到峰值強度時，此后，巖樣出現應變軟化現象。本文引用文獻[8]中的試驗機與巖樣聯合作用的力學模型作為頂底板－礦柱圍巖系統的力學模型，在此基礎上，將老頂作用在頂底板－礦柱圍巖系統的荷載簡化為集中荷載P，直接頂視為彈性介質用剛度為Km的彈簧來代替。礦柱可視為由剛度為KR的彈簧和具有塑性軟化性質的元件R組成。力學模型如圖1所示。

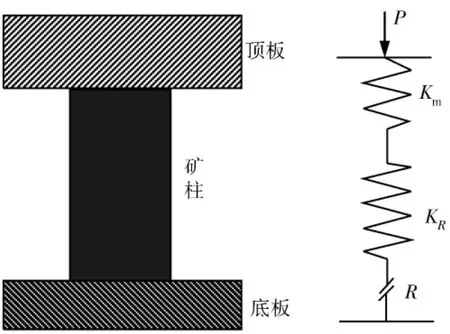
圖1 頂底板－礦柱圍巖系統力學模型

礦柱峰后塑性軟化的本構關系[9]：

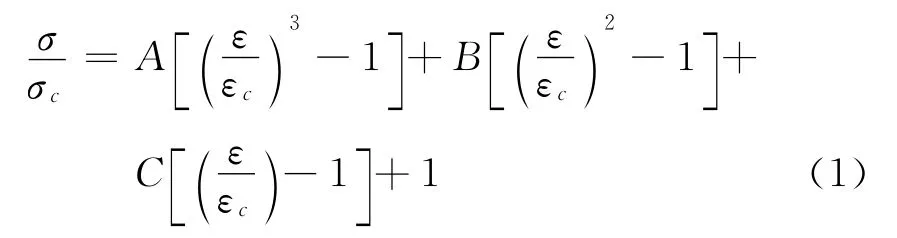
式中：A＝2（1－n）／（m－1）（m2＋m－2）；B＝－3Am／2；εg／εc＝m；σg／σc＝n；σc為峰值強度，MPa；εc為峰值強度對應的應變；σg為峰后曲線拐點處的應力，MPa；εg為峰后曲線拐點處應力對應的應變。

2 系統的勢函數

在研究巖石破裂失穩破壞的過程中發現，礦柱發生失穩破壞都是在其荷載－變形關系曲線峰值后發生的。巖石的變形失穩根源在于巖石應變弱化的非線性本構關系[1]。為了行文方便，假設礦柱高H，礦柱的塑性應變能相當于長寬為L，高為H的四方體全部發生塑性軟化變形的應變能。設直接頂得壓縮量為u1（剛度為Km的壓縮量），礦柱的壓縮量為u（剛度為KR的壓縮量），則老頂的下沉量為：（u1＋u）。由于模型中彈簧K、KR為串聯關系，當礦柱以準靜態被壓縮時可近似認為：Kmu1＝KRu。

集中荷載P對系統所做的功為：

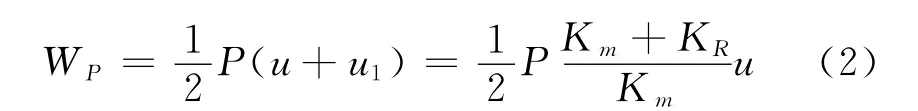
剛度為Km的彈簧的彈性能為：

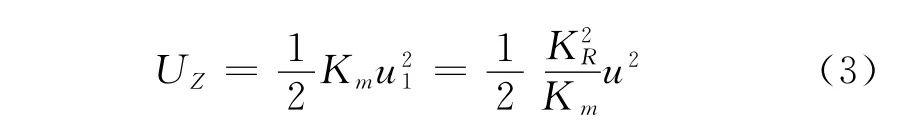
礦柱的應變能分為彈性應變能UE和塑性軟化應變能Us：

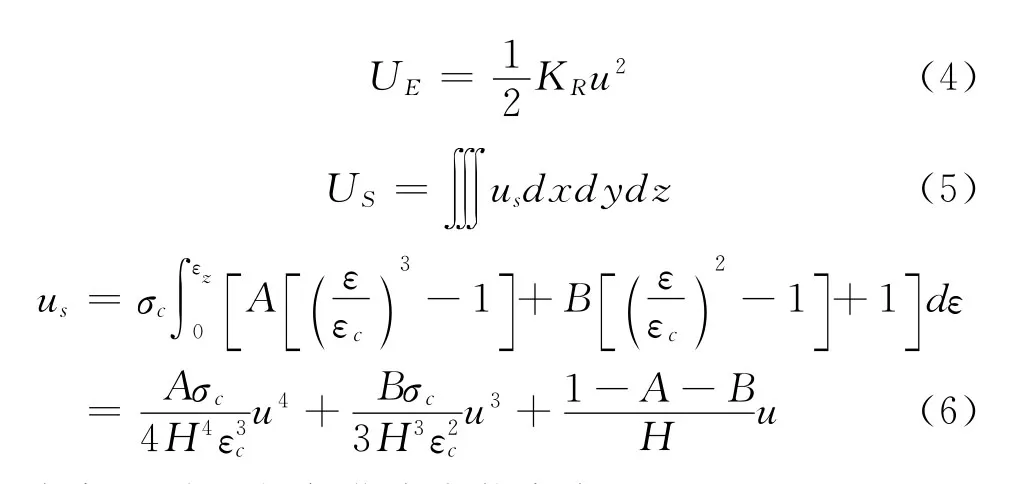
式中us為塑性軟化應變能密度。

將式（6）代入式（5）可得

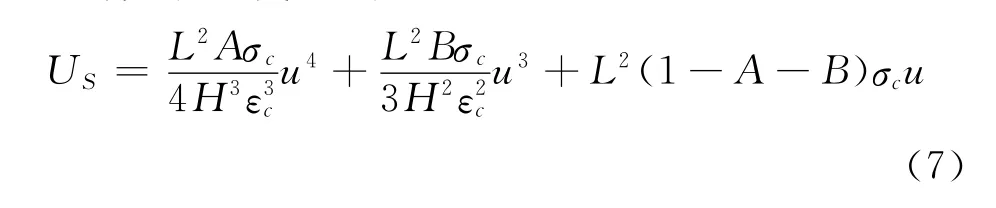
系統的總勢能為

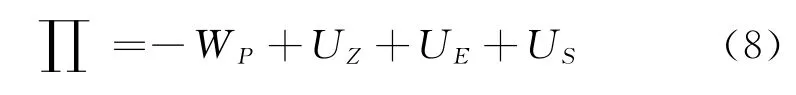
將式（2）、式（3）、式（4）、式（7）代入式（8）可得系統的總勢能為：

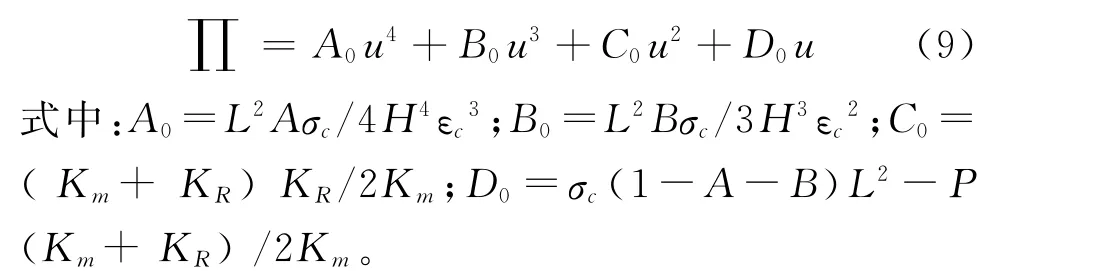
3 礦柱沖擊的突變模型

突變理論是法國數學家Thom于20世紀70年代初提出的，主要是研究某一系統或過程，由一種穩定狀態到另一種穩定狀態的躍進[10]。礦柱的突然失穩－巖爆具有尖點突變的五條典型性質，即突跳、滯后、發散、雙模態、不可達[11]。所以，本文用突變理論研究礦柱沖擊地壓。取礦柱的壓縮量u為狀態變量，從系統的總勢能函數可以看出礦柱發生失穩的啟動過程屬于尖點突變類型。

平衡曲面方程為：

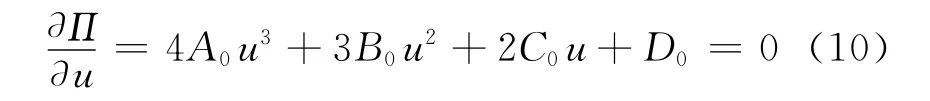
由平衡曲面的光滑性質，可知在尖點處有：

從而可得尖點：

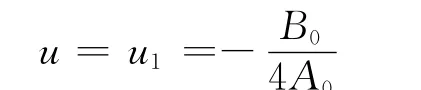
將平衡曲面方程在u1處進行Taylor級數展開，并將尖點值u1代人其中，按突變理論，截取前3次項不影響方程的定性性質，取無量綱量x＝（uu1）／u1，因此可將平衡曲面方程式（10）化為標準形式：

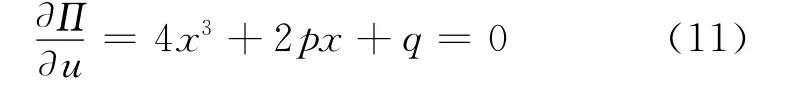
突變點集方程為：

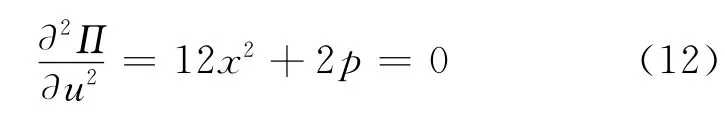
聯立式（11）、式（12）消去x可得分叉集方程為：

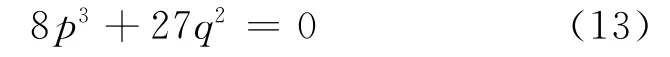
平衡曲面為一具有褶皺的光滑曲面，由上、中、下三葉構成，如圖2所示。其中上葉和下葉是穩定的，中葉是不穩定的。當p、q達到褶皺曲面的邊緣時，將會產生突變，這時系統處于不穩定狀態。在無擾動的情況下，分叉集的左支曲線為突變發生的臨界啟動條件。當控制變量p、q一旦超過臨界啟動條件，x將跳躍式的增大，這時系統將由準靜態破壞狀態進入失穩狀態。

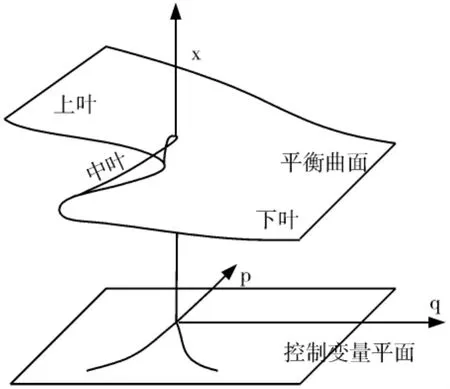
圖2 尖點突變模型

4 突變模型分析

由式（13）可知，當控制參數p、q在分叉集以外變化時，如圖3中箭頭所示，這時x只能以較小的值保持在下葉，不可可能跳躍到上葉，系統不會發生失穩破壞。只有當p≤0時，系統將發生突變，但是從圖2和是（13）可知當p＝0時，q＝0；這時，在外界的擾動下，系統雖然失穩，但是馬上就進入穩定狀態，所以這時不會發生沖擊地壓，當系統發生沖擊地壓時，系統的突變如圖4中箭頭所示。發生沖擊地壓的必要條件為：p＜0，即：

式中：Ec＝σc／εc；K1＝（Km＋KR）KR／Km。

由尖點突變理論可知：當控制變量p、q滿足分叉集方程時，系統才會發生失穩，分叉集方程是系統發生失穩的充要條件。并且當p＜0時，系統才會發生突變，沖擊地壓才能發生。故該系統發生失穩的充要條件為：

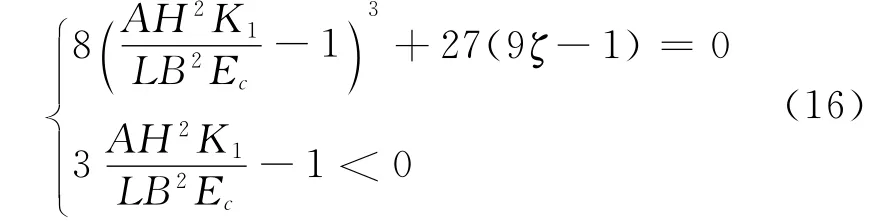
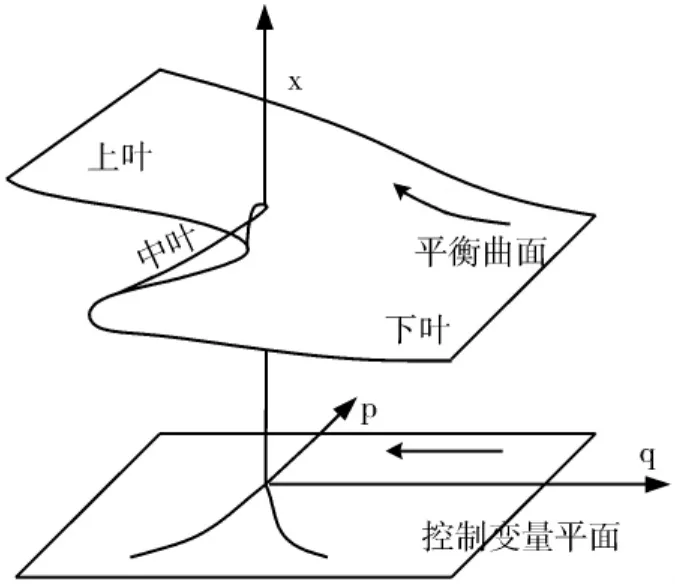
圖3 系統穩定時的平衡曲面與分支曲線

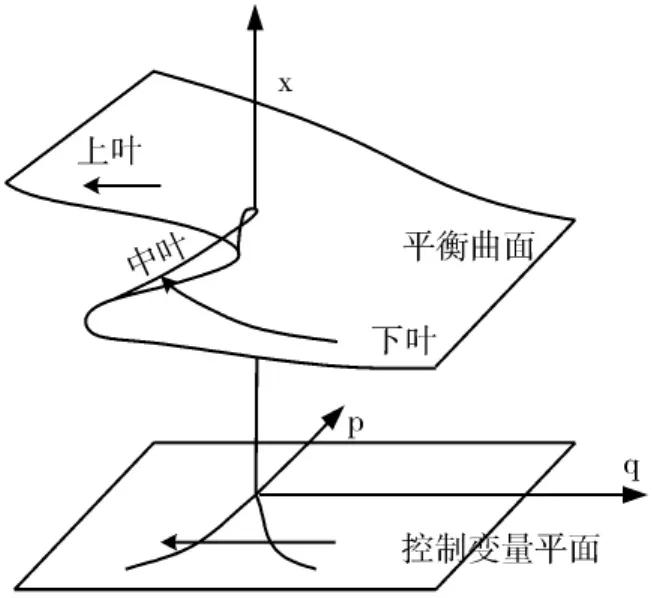
圖4 系統失定時的平衡曲面與分支曲線

由式（15）可看出只有在p＜0，即3AH2K1／LB2Ec－1＜0時，礦柱才能失穩發生沖擊地壓由此可以看出礦柱失穩與頂板巖層和礦柱本身的剛度、礦柱的幾何尺寸、礦柱達到應力峰值時的應力和對應的應變以及礦柱發生塑性軟化區域的大小有關，還與礦柱峰后曲線拐點處的應力應變有關，這些參數都是反映礦柱自身的材料性質，是影響礦柱穩定的內在因素。礦柱發生塑性軟化的區域越大且礦柱達到應力峰值時對應的應力和應變比值也越大，這樣就越容易發生礦柱沖擊地。由突變理論可知，只要把控制參數p、q控制在尖點區域以外就可以有效的防止突變的發生。

4 結束語

本文通過建立頂板－礦柱圍巖系統的力學模型；應用突變理論建立了圍巖－礦柱系統失穩發生沖擊地壓的尖點突變模型。應用突變理論得出了礦柱失穩的充要條件，礦柱失穩是由頂板巖層和礦柱本身的剛度、礦柱的幾何尺寸、礦柱達到應力峰值時的應力和對應的應變以及礦柱發生塑性軟化區域的大小、礦柱峰后曲線拐點處的應力應變等內在因素決定。在生產實際中只要合理布置礦柱尺寸大小，控制礦柱塑性軟化區域的發展，把控制參數p、q控制在尖點區域以外可以有效的防止礦柱沖擊地壓的發生。

[1]谷惠棠，胡慧明.基于突變理論的礦柱失穩破壞研究[J].金屬礦山，2011（8）：15－18.

[2]李忠華，潘一山.煤柱沖擊地壓的解析分析[J].地質災害與環境保護，2001，12（2）：62－65.

[3]王玉山.礦柱失穩破壞的力學模式研究[J].采礦技術，2011，11（3）：55－57.

[4]王存文，姜福興.煤柱誘發沖擊地壓的微震事件分布特征與力學機理[J].煤炭學報，2009，34（9）：1169－1173.

[5]李江騰，曹平.硬巖礦柱縱向劈裂失穩突變理論分析[J].中南大學學報：自然科學版，2006，37（2）：371－375.

[6]高明仕，竇林名.煤（礦）柱失穩沖擊破壞的突變模型及其應用[J].中國礦業大學學報，2005，34（4）：433－437.

[7]尤明慶，華安增.巖樣單軸壓縮的尺度效應和礦柱支承性能[J].煤炭學報，1997，22（1）：37－41.

[8]尤明慶.巖樣單軸壓縮的失穩破壞和試驗機加載性能[J].巖土力學，1998，19（3）：43－49.

[9]祝平.煤巖應變軟化特性與地下硐室穩定性分析[J].煤礦開采，1998（2）：41－44.

[10]王凱，俞啟香.煤與瓦斯突出的非線性特征及預測模型[M].徐州：中國礦業大學出版社，2005.

[11]費鴻祿，徐小荷，唐春安.狹窄煤（巖）柱巖爆的突變理論研究[J].中國礦業，1993，2（4）：57－61.