立式三軸攪拌釜固－液懸浮特性的數值模擬

趙麗君 尹 俠

（南京工業大學機械與動力工程學院，江蘇 南京 211816）

攪拌設備是現代工業生產中典型的過程設備之一，在石油化工、醫藥、食品、造紙、冶金、環保等行業都有著廣泛的應用。隨著計算流體力學（CFD）技術的發展，對給定條件下攪拌槽內流體的流動狀態進行預測已經成為可能，越來越多的學者采用此方法對攪拌槽內流場進行模擬［1，2］。

固液攪拌是工業攪拌設備中比較常見的一種操作，且固液懸浮作為兩相流問題要比單相流復雜得多，近幾年對其研究漸漸增多。對于立式單軸攪拌槽內固液混合過程的研究已較成熟［3－5］，但對立式多軸攪拌槽內固液混合過程的模擬還未見報道。相比于傳統的立式單軸攪拌槽，立式三軸減小了槳葉加工的難度，降低了對攪拌軸強度以及減速器的要求，并且降低了設備的制造成本［6］。本試驗利用FLUENT軟件對立式三軸攪拌釜內的兩相混合進行了數值模擬，得到攪拌槽中液體的流動狀況和固相分布情況。對固液兩相流的流場分布規律進行研究，得到最佳攪拌速度和完全離底懸浮所需最低攪拌功率。為此種結構的工業設計提供一定的參考。

1 數學物理模型和計算模擬方法

1.1 攪拌器模型

為驗證數值模擬方法的可靠性，建立計算物理模型如下：攪拌槽為圓柱型平底容器，直徑（D）2m，高（H）0.8m。攪拌槳槳型CBYIII（槳徑d＝0.174m），三槳均布。液位高度HL＝0.6m，兩物相系采用玻璃珠－水體系，固體體積分數為0.11，直徑為50～150μm，其幾何模型見圖1。計算時采用非結構化網格（見圖2），其網格數為586 318。

1.2 多相流模型

采用歐拉－歐拉模型描述固液兩相流，歐拉－歐拉法是把顆粒作為擬流體，認為顆粒與流體是共同存在相互滲透的連續介質，顆粒與流體之間的藕合是通過動量交換項以及連續相作用在分散相上的曳力得到的。且固液兩相間動量交換使用Wen－Yu模型，其連續性方程和動量方程如下［7］：

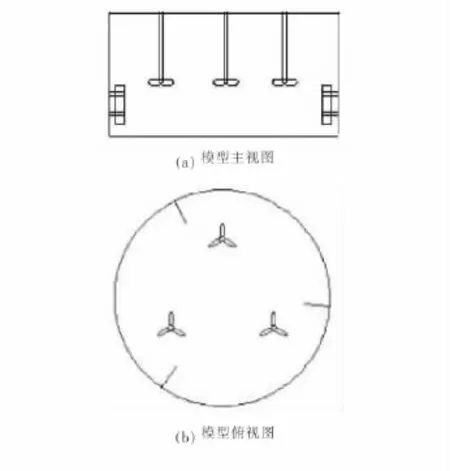
圖1 立式三軸攪拌釜幾何模型Figure 1 Geometric model of vertical three－impeller stirred tank

圖2 攪拌釜內的網格劃分Figure 2 Grids for the stirred tank

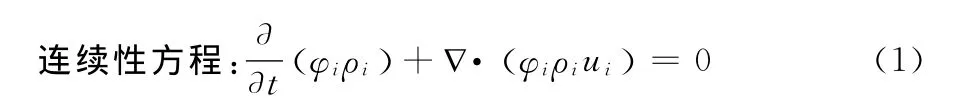
連續相和離散相動量方程分別為：

其中兩相間動量交換因數Ksl：

曳力系數CD：

式中：

φi—— 物相體積分數，%；φl——液相體積分數，%；

φs——固相體積分數，%；

ρi—— 物相密度，kg／m3；

ρl—— 液相密度，kg／m3；

ρs—— 固相密度，kg／m3；

ui—— 物相速度矢量，m／s；

ul—— 液相速度矢量，m／s；

us—— 固相速度矢量，m／s；

τl—— 液相壓力應變張量；

τs——固相壓力應變張量；

g—— 重力加速度，m／s2；

ds——固體顆粒直徑，m；

Res—— 雷諾數；

P——功率，W。

1.3 計算模擬及邊界條件

采用FLUENT6.3軟件對攪拌器內的兩相混合進行數值模擬，選用三維穩態求解器，液相湍流模型采用標準k－ε模型，計算采用多重參考系法（MFR），配合歐拉－歐拉多相流模型。壓力速度耦合采用SIMPLEC算法，差分格式使用一階迎風，殘差設為1e－6。計算時監視變量（速度、槽底平均固含率）趨于穩定值時認定為計算收斂。

2 數值模擬結果分析

2.1 CFD模擬的流場固相濃度分布

在攪拌過程中，固相粒子受兩個力的作用：① 流體流動的剪切力；② 固體顆粒本身的重力。最終固體粒子沉積的位置為這兩個力綜合作用的結果。改變槳葉攪拌速度分別為330，440，550r／min，折合葉端線速度分別為3，4，5m／s。分別對其進行模擬，達到計算收斂時觀察槽底固體濃度分布見圖3。由圖3可知，隨轉速的增大，沉積面積越來越小，槽底固相平均濃度逐漸降低，槽中心濃度也逐漸降低。3個槳葉的正下方均有一片低固含率區，對應著圖5中的由葉輪排出流撞擊槽底形成的高速區；而兩個攪拌器之間存在顆粒沉積區，此區的流場速度主要由葉輪底部流體與其傳質形成，速度相對較小，易造成顆粒沉積，但隨著轉速增大，沉積面積逐漸減小至消失；對于槽底兩槳葉間靠近槽壁的區域，由于本試驗采用平底模型，此區域易產生攪拌死區，但隨著轉速的增大，此區域面積也越來越小。所以為了減小攪拌死區，可以適當增大槳葉葉端轉速。由此規律和現象可以看出：CFD模擬結果中槽底沉積帶的大體形狀和位置與試驗結果有較好的一致性。

2.2 固體粒子對流場的影響

圖4為攪拌槽在轉速N＝550r／min攪拌時，雙槳葉面單相流場與多相流場速度圖。由圖4可知，由于固體粒子的加入，槳葉排出流的錐形角變大，槽中心處的軸向流變得并不明顯；整體循環在單相中約為0.8 HL，但在多相中僅達到0.4 HL高度時變折回槳葉區，對應固體懸浮高度約為0.4 HL，這將導致槽體上端固相濃度較低。所以當攪拌軸結構與安裝位置選取不當時中心部分速度較小，易造成中心部分出現固相堆積。

圖3 不同葉端線速度下模擬（左）與試驗（右）槽底固相濃度分布圖Figure 3 Solid phase concentration distribution under different agitating blade tip speed at the groove bottom for simulation（left）and experiment（right）

圖4 速度為550r／min時單相流和多相流場的速度矢量圖Figure 4 Speed vector－graph for single－phase flow and multiphase flow field at speed 550r／min

為了更清楚的描述攪拌流場中的速度矢量，對單相流場和多相流場攪拌槽槽底z＝0m和液面z＝0.6m橫截面分別進行截取，其速度矢量圖見圖5。從z＝0m截面圖中可以看出：槽底在攪拌器正下方的速度矢量是向斜上方四周發散的，這使得槽底流體向上方及四周運動，對于槽底顆粒達到完全離底懸浮是很有幫助的；且多相較單相，槽中心及兩槳葉間靠近槽壁的區域速度值明顯降低。所以在這些區域中固體粒子容易堆積。從z＝0.6m即液面速度矢量圖可以看出：多相速度受各自攪拌槳影響比單相小，開始繞著攪拌槽中心整體旋轉，軸向運動變得很微小。所以將導致攪拌過程中，其與槽下方傳質較少，濃度較低。當攪拌速度不夠時，不易于槽內整體固相的均勻懸浮。

圖5 單相與多相流場中各橫截面的速度矢量圖Figure 5 Speed vector－graph for multiphase flow and single－phase flow at different cross－sections

3 最佳轉速和最小功率的分析

3.1 臨界離底懸浮轉速的分析

利用文獻［8］中的濃度判據分析攪拌槽完全離底懸浮臨界轉速。其原理：單層球狀固體顆粒堆積在一起時，固體顆粒體積分數若大于π／6（約52%）就說明固體顆粒沒有完全懸浮，局部有堆積現象。即可以用局部固相體積分數的最大值φsmax作為完全離底懸浮的判據。

不同轉速下槽底最大固相體積分數φsmax的模擬結果見圖6。由圖6可以看出此結構下臨界懸浮轉速Njs為635r／min。即當攪拌速度大于635r／min時，槽內達到完全離底懸浮狀態。

3.2 最佳轉速和攪拌最低功率的分析

基于CFD方法的攪拌功率的計算公式：

式中：

P—— 攪拌功率，W；

M—— 扭矩，N·m；

N—— 轉速，r／min；

圖6 不同轉速下槽底最大固相體積分數φs maxFigure 6 Maximum solid volume fractionφs maxunder different rotation speeds at the tank bottom

ω—— 槳葉旋轉角速度，rad／s。

對于三軸模型，扭矩為三軸扭矩之和，而各軸扭矩又包括攪拌槳扭矩Mi和攪拌軸扭矩Ms，即

單位體積功率表達式為：

式中：

v—— 攪拌釜內固液流體體積，由體積公式v＝π（D／2）2HL求得v＝1.884m3。

由CFD結果得出各扭矩并計算單位體積功率和槽底平均固相濃度，具體數值見表1。

分析得出單位體積功率和槽底平均固相濃度隨轉速的變化具體情況見圖7。

由圖7可知，在相同的攪拌釜結構中，隨著轉速的增加，單位體積功率逐漸變大，即攪拌能耗逐漸變大；且此變化趨勢成指數增加，即能耗隨轉速的提高比轉速本身提高得更快。而槽底平均固相濃度則隨著轉速的增加逐漸變小，且其減小的速度沒有轉速增長的速度快。所以可以得出以下結論：轉速越快，能耗越高，懸浮效果越好；轉速越慢，能耗越低，懸浮效果越差。但為了改善懸浮效果，一味提高轉速并不是最好的辦法，因為轉速增加到一定程度，隨轉速的提高，能耗增加得很快，而懸浮效果改善得較慢。所以根據此規律找出既能達到懸浮效果，又能消耗最低的功耗的最佳轉速。

表1 不同轉速下扭矩、單位體積功率及槽底平均固相濃度計算結果Table 1 The results of torquemoment，specific volume power and mean solidconcentration at bottom tank under different rotation speeds

圖7 單位體積功率和槽底平均固相濃度隨轉速的變化曲線圖Figure 7 Variation trend of the specific volume power and mean solid concentration at bottom tank with the speed

綜合上述結論和圖7可知，兩曲線的交點處，轉速約為640r／min，略大于Njs，固此轉速已能使攪拌槽中固相達到完全離底懸浮。所以可以選取此點轉速作為攪拌時的最佳轉速，此點的功耗作為最低的攪拌功率。即最佳轉速為640r／min，最低攪拌功率為395.6W。

4 結論

用CFD數值模擬方法對立式多軸攪拌槽內固液懸浮性能進行研究，對槽內固體顆粒的分布規律進行分析，并討論了不同轉速對最大固相體積分數，單位體積功率和槽底平均固相濃度的影響，主要結論如下：

（1）利用CFD模擬預測的不同轉速下槽底固相顆粒沉積帶的形狀和位置與試驗結果相似，表現出較好的一致性；槽底中心和槽底兩槳葉間靠近槽壁的區域易產生固相堆積，隨著轉速增加，沉積面積越來越小。

（2）對于單相體系，固體粒子的加入抑制了槽內軸向循環流的高度，且槽內液體總體速度明顯降低。槽體上部流型為繞槽軸向的水平循環流，不利于槽內整體固相的均勻懸浮。

（3）在固含率為11%的槽內利用濃度判據，找出完全離底懸浮臨界轉速Njs為635r／min。

（4）利用CFD模擬并計算，分析得出單位體積功率和槽底平均固相濃度隨轉速的變化規律，找出既能達到懸浮效果，又能使功耗最小的最佳轉速約為640r／min，此時所需最低攪拌功率為395.6W。

1 張少坤，尹俠.雙層槳攪拌槽內流場的數值模擬［J］.食品與機械，2011，27（1）：71～73.

2 方鍵，桑芝富，楊全保.側進式攪拌器三維流場的數值模擬［J］.石油機械，2009，37（1）：30～34.

3 陳道芳，徐雷興，陳甘棠，等.固、液系機械攪拌槽中顆粒懸浮特性的研究［J］.化學反應工程與工藝，1992（3）：44～53.

4 銀建中，程紹杰，賈凌云，等.攪拌式反應器內固－液兩相懸浮特性的CFD模擬［J］.應用科技，2009，36（11）：11～16.

5 董厚生，魏化中，舒安慶，等.攪拌槽內固液兩相流的數值模擬及功率計算［J］.化工裝備技術，2012，33（1）：14～16.

6 李永綱，黃雄斌.立式圓槽內多軸攪拌器固－液懸浮性能［J］.過程工程學報，2012，12（2）：181～186.

7 劉冠一.側入式攪拌中固液懸浮的數值模擬［D］.濟南：山東大學，2010.

8 鐘麗，黃雄斌，賈志剛.固－液攪拌槽內顆粒離底懸浮臨界轉速的CFD模擬［J］.北京化工大學學報，2003，30（6）：18～22.