基于小波分析的電力電纜故障檢測方法研究

石黃霞，黃 卉

(新疆工程學院，烏魯木齊 830091)

1 引言

隨著電力行業(yè)的發(fā)展，各種電纜越來越多地運用到生產生活的各個領域中。因此，電力電纜的安全運行對于電力系統(tǒng)供電的可靠性起著舉足輕重的作用。而電纜一般都埋入地下或進入電纜溝敷設，在施工安裝、運行過程中經(jīng)常因短路、過負荷運行、絕緣老化或外力作用等原因造成故障。因此，如何快速準確的檢測診斷故障，及時對電纜進行合理的維護、檢修及更換，盡快使供電系統(tǒng)恢復正常，對保障電纜可靠運行具有重要意義。

目前，成熟的技術只適用于離線檢測方面，對于電力電纜運行狀態(tài)的在線檢測提出了許多檢測方法，但一直沒有取得令人滿意的效果。常用的電力電纜檢測和診斷方法有:直流法、工頻法、低頻法、復合判斷法［1］。這些方法都要處理系統(tǒng)異常或故障時，各種含有大量短時沖擊及突變成分的實時信號［2］。這些信號中，其奇異性包含了豐富的信息，具有區(qū)別于正常時穩(wěn)態(tài)信號明顯、突出的特征，若能充分利用這些特征，將有利于故障的及時檢測。而近年來較流行的小波變換方法恰好可滿足電力系統(tǒng)中對突變信號分析的要求，為最終實現(xiàn)有效的電力系統(tǒng)在線檢測與診斷系統(tǒng)提供技術保證。主要對在線監(jiān)測的低頻交流電壓疊加法［3］測試得到的故障信號，運用小波分析檢測出信號的奇異點，并分離出標志電纜劣化信息的電壓信號。

2 小波分析基礎

2.1 小波變換的定義

小波變換不僅具有時間和頻率局部化特性，而且可以對信號做奇異性分析。在做奇異性檢測時，選擇連續(xù)小波變化，連續(xù)小波變換定義［4－5］為:

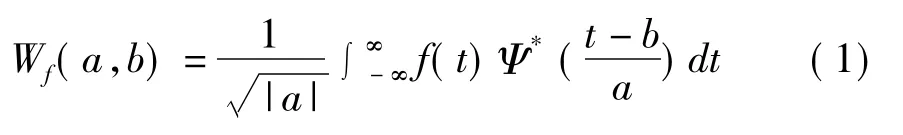
式中:f(t)是一個時間域函數(shù);Ψ(t)為分析小波;b為位移因子;a為尺度因子;Wf(a，b)為小波變換系數(shù)。

2.2 信號奇異性的定義

若信號在某一點或某一個區(qū)域內是可微的，則該信號在該點或該區(qū)間內是規(guī)則的，反之，則是奇異的。在數(shù)學上，Lipschitz指數(shù)被用來定量地描述函數(shù)的奇異性，簡稱李氏指數(shù)。

設n是一非負整數(shù)，n＜a≤n+1，如果存在兩個正常數(shù)A和h0，次多項式Pn(h)，使得對任意的h≤h0均有:

|f(x0+h)－Pn(h)|≤A|h|a

則稱f(x)在點x0處為Lipschitz a。

如果上式對所有x0∈(a，b)均成立，且x0+h∈(a，b)，稱 f(x)在(a，b)上是一致 Lipschitz a。

Lipschitz a指數(shù)越大，函數(shù)越光滑;函數(shù)在一點連續(xù)、可微，則在該點的Lipschitz a指數(shù)為1;函數(shù)在一點可導，而導數(shù)有界但不連續(xù)時，Lipschitz a指數(shù)仍為1;如果f(x)在x0的Lipschitz a指數(shù)小于1，則稱函數(shù)在x0點是奇異的。一個在x0處不連續(xù)但有界的函數(shù)，該點的 Lipschitz a指數(shù)為0［6］。

在利用小波分析這種局部奇異性時，小波系數(shù)取決于f(x)在x0的領域內的特性及小波變換選取的尺度。

2.3 信號奇異性檢測

利用小波變化對信號奇異性進行檢測，可以確定奇異點位置，另外，選用合適的小波函數(shù)與尺度可對奇異點的奇異特征進行精確描述［7］。

對小波變換結果進行分析，選擇信號和噪聲具有不同能量分布及能量變化趨勢的幾個連續(xù)尺度為特征尺度。由于在較大尺度上的小波變換模極大值點主要屬于有效信號的奇異點，因此從所選取的最大尺度開始尋找奇異點。

3 小波分析在電力電纜故障檢測中的應用

常用的電力電纜檢測和診斷方法有:直流法、工頻法、低頻法、復合判斷法。采用低頻交流電壓疊加法進行測量。

如圖1所示，在電纜的屏蔽層上疊加101Hz的交流電壓，監(jiān)測樹枝劣化而產生的1Hz的劣化信號。由于在樹枝劣化的電纜上疊加2倍工頻+1Hz(近似值)電壓時，被測的劣化信號最大，可根據(jù)這種方法檢測出1Hz的劣化信號的強弱來判斷電纜劣化的程度［8］。

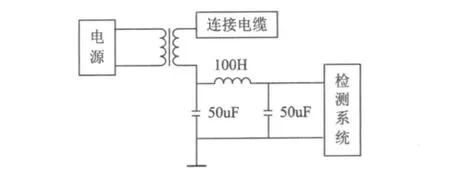
圖1 低頻交流電壓疊加法測量系統(tǒng)連接圖

3.1 故障信號分析

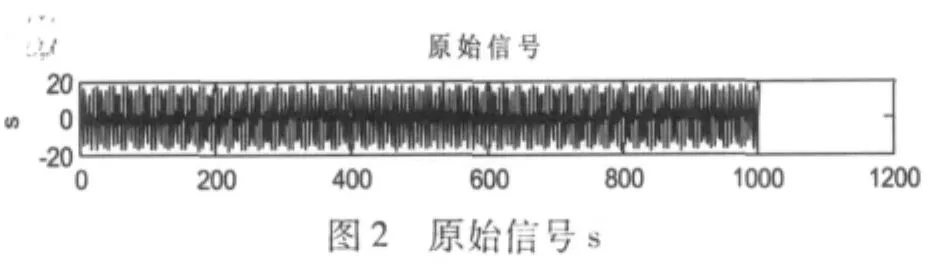
低頻交流電壓疊加法得到的電壓信號由1Hz、50Hz、100Hz的正弦波和測量過程中的隨機噪聲疊加而成，其中1Hz正弦波相對于100Hz正弦波較微弱。在傳統(tǒng)的處理方法中，信號被處理之前先用硬件電路將高頻部分(噪聲和100Hz)濾波，剩下1Hz和50Hz的疊加波形，再通過程序將1Hz波形從疊加波形中分離出來。這種方法既要用到硬件電路，又要用軟件編程，而且效果不佳。文中運用Matlab7.5中的小波工具箱函數(shù)，實現(xiàn)故障信號奇異點的檢測和特定頻率信號的提取。故障信號s在采樣的200點以前包涵50Hz、100Hz和噪聲，200點以后出現(xiàn)了1Hz的信號。

3.2 故障信號檢測及分析結果

核心程序中運用的Matlab7.5中的小波工具箱函數(shù)［9］:

［a，d］=wavedec(s，5，＇db5＇);% 對 s 信號選用db5小波函數(shù)進行5層分解;

a(i)=appcoef(a，d，＇db5＇，i);% 提取小波分解的第i層低頻系數(shù);

d(i)=detcoef(a，d，5);%提取小波分解的第i層高頻系數(shù);

dd(i)=wrcoef(＇d＇，a，d，＇db5＇，i);% 重構第 i層高頻信號;

aa(i)=wrcoef(＇a＇，a，d，＇db5＇，i);% 重構第 i層低頻信號;

小波工具箱函數(shù)要根據(jù)對信號不同的處理要求來選擇，在檢測信號突變時，短的小波比長的小波更為有效，這點Haar小波或db1小波就足夠了。考慮到識別不同頻率的信號，文中選用了db5小波。

采樣到的原始故障信號s如圖2所示。程序運行的分析結果如圖3－圖5所示。

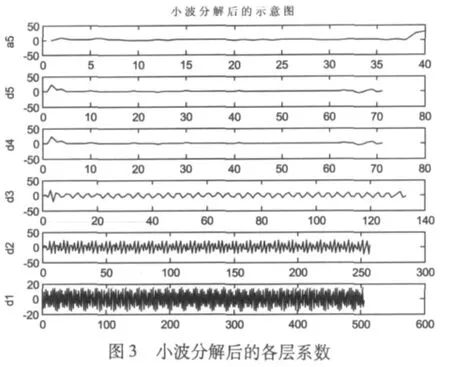
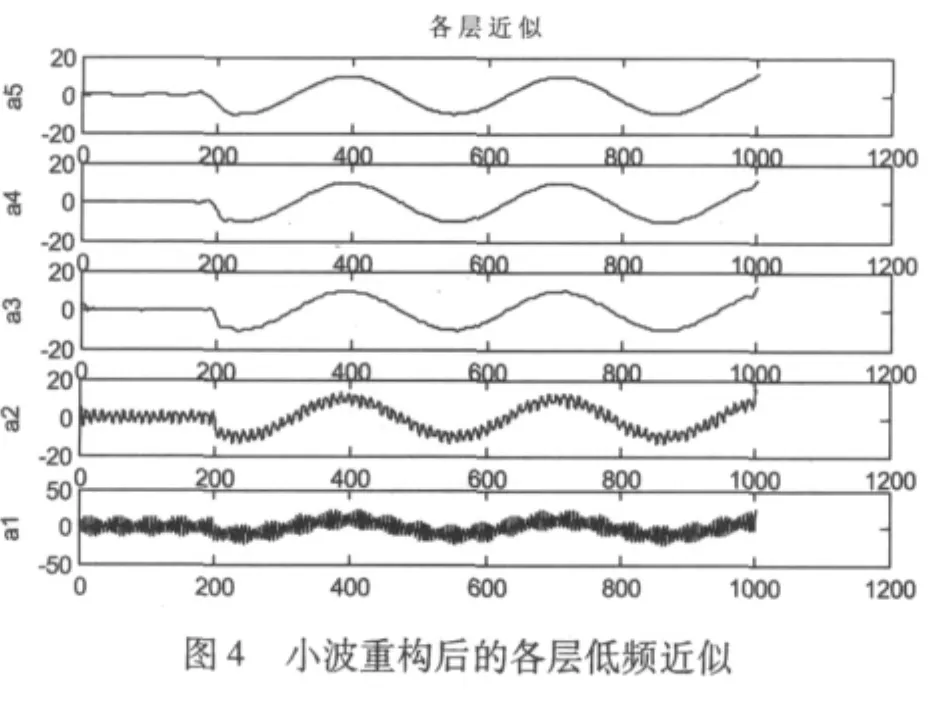
在小波分解中，各層小波分解可以看作是帶通、高通或者低通濾波器，不同尺度具有不同的時間和頻率分辨率。由圖5的d4、d5層可以看出，在200點時由于信號突變導致Lip指數(shù)A減小，信號的奇異性增大，在此處出現(xiàn)了一個間斷點。從圖4和圖5中可以看到，a2、d2和a3、d3分別表示了100Hz和50Hz的頻率信息，放大后可以看到d2的頻率是d3的2倍。1Hz的頻率相對于50Hz和100Hz的頻率很小，因此在分解的第一層系數(shù)a1就可看出不連續(xù)性，從d4、d5能夠更明顯清晰的看出200點處出現(xiàn)的間斷點，即為故障點。將a4、d4放大即可觀察到頻率近似為1Hz的低頻信號。

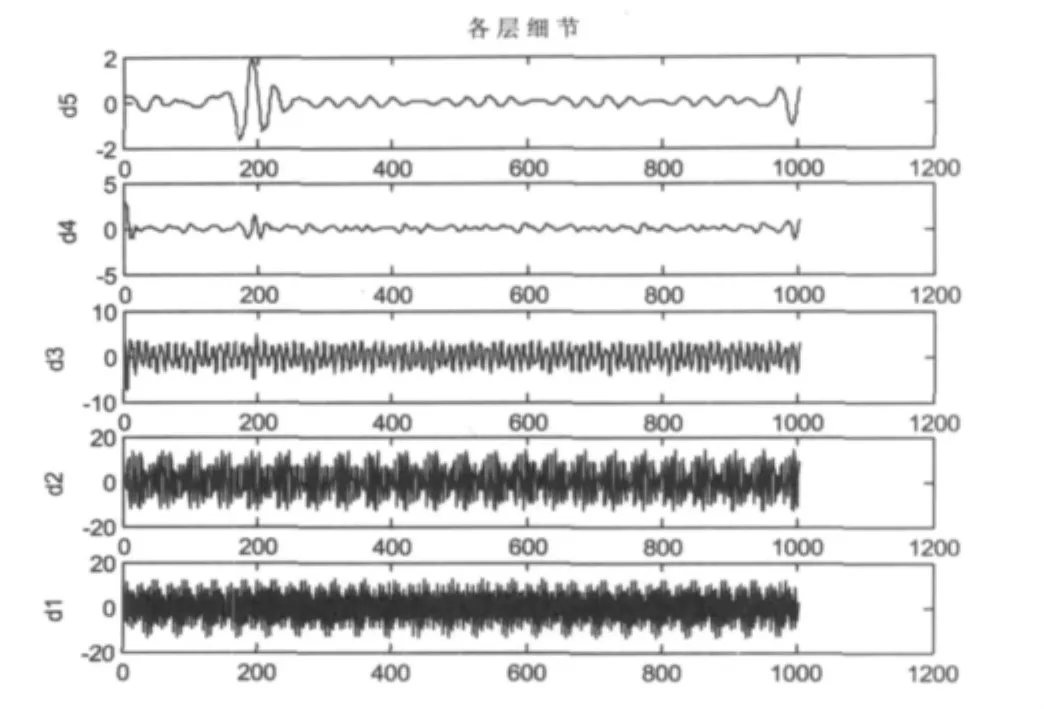
圖5 小波重構后的各層高頻細節(jié)

4 結 束 語

針對電纜狀態(tài)檢測過程中大量的暫態(tài)信號依靠傳統(tǒng)方法難于充分分析處理的問題，提出運用一維離散小波工具箱函數(shù)分析含有故障信息的電壓信號的方法。根據(jù)電壓信號的奇異性并包含的狀態(tài)信息，確定了信號產生奇變點的位置和提取出標志電纜劣化程度的1Hz電壓信號。和傳統(tǒng)方法相比，不需要前置高通濾波器等硬件支持，只需調用小波工具箱函數(shù)即可。

［1］劉耀南，邱昌容.電氣絕緣測試技術［M］.北京:機械工業(yè)出版社，1994.

［2］徐丙根，李勝祥，陳宗軍.電力電纜故障探測技術［M］.北京:機械工業(yè)出版社，1999.

［3］(美)C.Sidney Burru(譯).小波與小波變換導論［M］.北京:機械工業(yè)出版社，2008.

［4］李媛.小波變換及其工程應用［M］.北京:北京郵電大學出版社，2010.

［5］周龍.電力電纜絕緣監(jiān)測中的低頻交流電壓疊加法研究［J］.電線電纜，2004，12(6):30 －32.

［6］張德豐.MATLAB小波分析［M］.北京:機械工業(yè)出版社，2009.

［7］陳中，趙聯(lián)文.信號奇異性檢測中小波分析的應用［J］.重慶大學學報(自然科學版)，2004，21(2):15－27.

［8］劉偉，曹思遠.基于小波變換的信號奇異性檢測在層位識別中的應用［J］.石油地球物理勘探，2010，45(4):530－534.

［9］淮文軍，王明芳，汪梅.基于小波分析的電纜故障特征提取方法研究［J］.計算機技術與發(fā)展，2007，17(11):209－211.