燃氣輪機動態仿真容積效應法研究
梁 超,吳新躍
(海軍工程大學 動力工程學院,湖北 武漢 430033)
0 引 言
利用數學模型代替真實燃氣輪機作為被控對象進行性能研究,是具有一定準確性且經濟性好的方法。在對燃氣輪機進行仿真時,文獻[1-5]都采用模塊化建模方法進行仿真。在對燃氣輪機進行穩態分析計算時一般都采用流量法進行計算[6-7],通過對每個模塊的輸入輸出流量平衡和轉子產生和消耗功率的平衡建立非線性方程組,需要用牛頓-拉弗遜(N-R)等迭代算法求解。在進行動態分析時,因為迭代算法需要反復進行迭代計算,為了提高實時性,采用容積效應法建立容積模塊消除計算時的迭代過程,即可以縮短計算時間,又能保證模型的計算精度。
本研究通過對容積效應法原理進行分析,提出運用容積效應法時更合理的容積大小的計算方法。
1 容積模塊的建立
在對三軸燃氣輪機動態建模中,主要解決低高壓氣機之間,高壓壓氣機與燃燒室之間,高、低壓渦輪間,低壓與動力渦輪間4 個管道間的流量不平衡問題,故在這4 個模塊間加入容積模塊,通過對容積模塊的計算,實現整個系統的流量平衡,模型示意圖如圖1 所示。
容積模塊代表的是具有一定當量容積的純流動部分,如圖2 所示。設一股總壓分別為P in,T in,W in 的流體流入容腔,以Pout,Tout,Wout流出。在動態過程中,容腔內有質量、能量的積聚和動量的變化,進出口參數將不再相等。對單純的流動連接部分,動態計算中主要考慮因流入流出流量差而引起的壓力的變化,系統計算達到平衡,從而消除計算的迭代過程。建模過程中,假設容積內流體同外界的傳熱及進出口的壓差很小可以忽略,只考慮質量的累積而引起的壓力變化。

圖1 三軸燃氣輪機模塊化模型
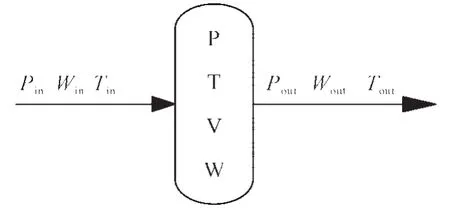
圖2 容積模塊示意圖
對部件間容積環節作如下假設:
(1)流動方向上的無傳熱量;
(2)容積大小不變。
基于容積模塊假設,有Tout=Tin。則有質量守恒方程式:

式中:Rg—氣體常數,J/(kg ·K);V—容腔體積,m3;P—容積模塊內壓力,Pa。T—模塊內溫度,K;Win,Wout—模塊入口,出口的質量流量,kg/s。
2 基于容積法的三軸燃氣輪機模型的建立
基于Matlab/Simulink 平臺建立燃氣輪機各個模塊模型的方法在文獻中已有詳細的介紹,這里直接給出在Matlab/Simulink 平臺上建立的三軸燃氣輪機的最終模型,如圖3 所示。
3 對容積效應法參數的討論
3.1 真實容積大小情況下的容積效應法計算
在實際建模中,V 一般認為是各個管路連接段和燃燒室的容積大小[8-10]。但在對三軸燃氣輪機建模過程中發現,如果采用實際容積作為容積大小的由來的話,以某型燃氣輪機高低壓渦輪間的容積模塊計算為例分析,兩渦輪間的體積大小為0.02 m3,1.0工況時高壓渦輪進口壓力為1.9e6 Pa,出口壓力為0.74e6 Pa,出口溫度為T=1.24e3 K,燃氣氣體常數為Rg=284.7 J/(kg ·K),則當流量差為0.01 kg/s 時,有:

從式(2)可以看出當流量差為0.01 kg/s 時,壓強的改變量可以達到1.7 個大氣壓左右,從而對高壓渦輪的下一步膨脹比誤差ΔPR 為:

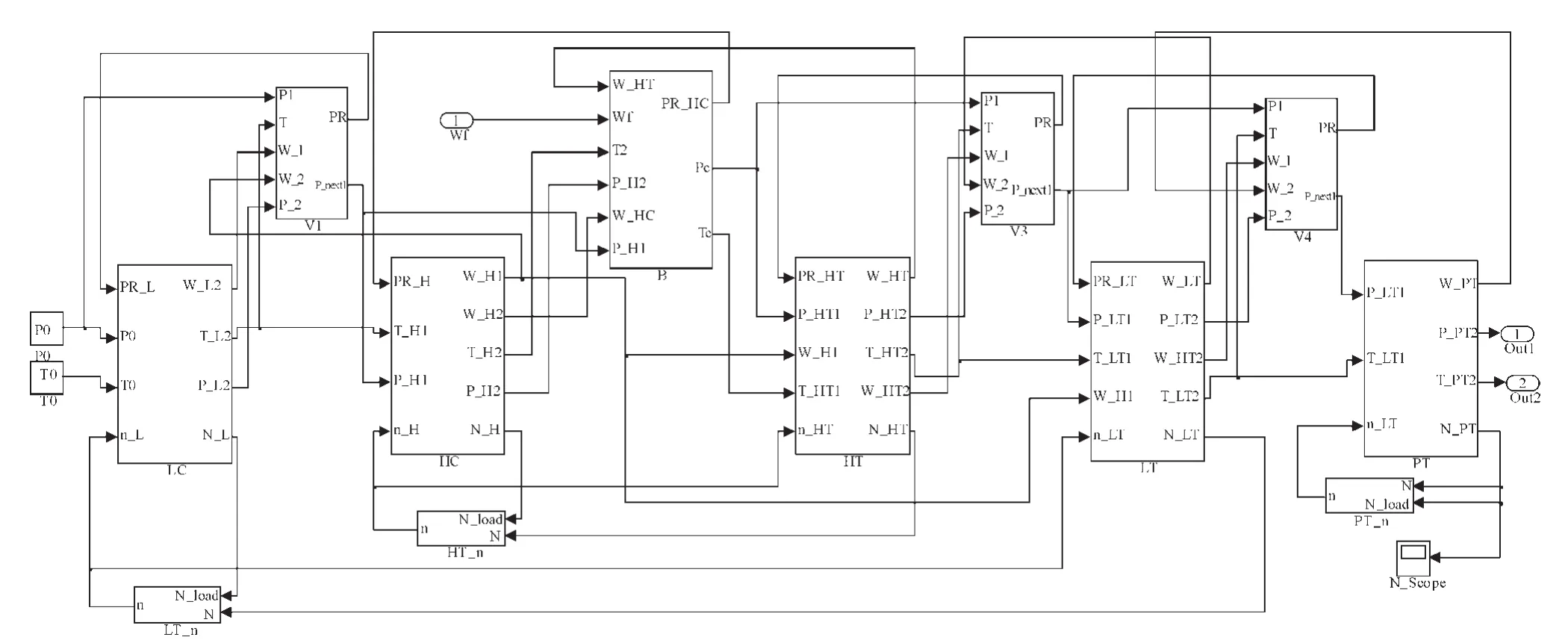
圖3 基于MATLAB/SIMULINK 的三軸燃氣輪機模型
這樣各個模塊誤差的累積將對最后的計算結果的收斂性產生很大的影響。現結合Matlab/Simulink 建立的模型,將4 個容積模塊的體積設置為真實管道的體積大小,容積模塊模型如圖4 所示。計算燃機從1.0工況運行到0.6 工況的過程即輸入燃油量的變化。已知實際0.6 工況下動力渦輪輸出功率為15 126 kW,計算得出的動力渦輪輸出功率變化如圖5 所示。

圖4 真實體積下的容積模塊模型

圖5 真實體積下燃氣輪機1.0 工況運行0.6 工況過程動力渦輪輸出功率
從圖5 可以看出,在用真實管道體積大小計算容積效應法時,燃機輸出功率的趨勢是符合現實規律的,但運行過程中計算結果上下波動很大,大小無法確定,誤差為計算真值的±0.2/1.51 即±14.3%以內,這樣的計算結果在實時預測來說是不可以接受的,也無法為后續的計算提供穩定精確值。
3.2 虛擬容積大小的容積效應的計算
通過前面計算結果可以看出,容積效應法計算時運用實際容積大小得到的結果是不符合規律、不理想的。一般對這種情況的處理是將氣體常數定為“kJ/(kg ·K)”,從而使計算結果振蕩縮小“1e3 倍”,從而使結果達到穩定值。但筆者認為,容積模塊的加入是為了取消迭代過程,達到各個模塊間的流量平衡,符合運行規律,則對容積大小的選擇應符合熱力學方程式:

此時,容積大小應為容積模塊入口的4 個變量(P、T、m、Rg)計算得出,容積模塊的計算條件為體積不變的情況下。如果采用實際體積的大小計算,是不符合熱力學規律的。同樣,本研究在基于Simulink 平臺上對容積模塊進行相應的改動后的容積模塊模型如圖6所示。
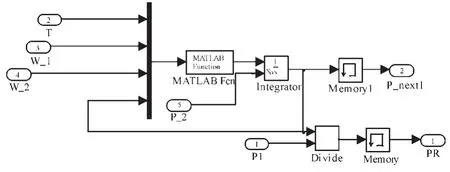
圖6 虛擬容積下的容積模塊模型
從模型中可以看出,每次計算時的容積大小是計算出來的結果,是變化的。在相同的供油律下運行整體燃機系統模型后動力渦輪的輸出功率變化如圖7 所示。

圖7 虛擬體積下燃氣輪機1.0工況運行0.6工況過程動力渦輪輸出功率
從圖7可以看出,計算結果趨勢正確,曲線光滑且收斂。兩種方法的計算結果如表1 所示。
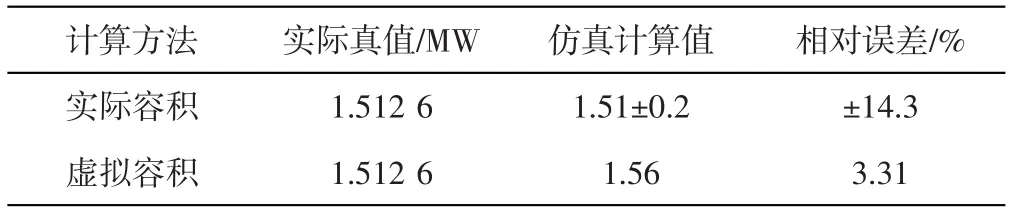
表1 兩種計算方法結果比較
從表1 中可以得出,采用虛擬容積大小計算時結果收斂度和精確度更高,也可以為后續計算提供準確的穩定值。
4 結束語
本研究采用容積效應法建立燃氣輪機實時動態模型,并采用Simulink 平臺建立模型求解,取消了為保證流量平衡條件下的計算迭代過程,保證了算法的有效性;
針對“容積效應法運用過程中,使用真實體積運算時計算結果振蕩較大,無法對燃氣輪機動態過程進行實時有效的運算”的問題,本研究對容積效應法的原理進行分析,提出采用虛擬容積計算方法計算容積大小。計算結果表明,采用虛擬容積大小計算條件下的動態仿真模型的計算結果精度更高,結果更穩定。
(References):
[1]張學鐳,王松齡.簡單循環燃氣輪機系統建模及其變工況性能分析[J].動力工程,2006,26(5):619-623.
[2]史霖鑫,臧述升.基于SIMULINK 的氣墊船三軸燃氣輪機的動態仿真[J].燃氣輪機技術,2006,19(3):37-39.
[3]常 雋,屈衛東.基于MATLAB/SIMULINK 的燃氣輪機系統動態模型仿真研究[J].微型電腦應用,2010(6):41-44.[4]敖晨陽,張 寧,陳華清.基于MATLAB 的三軸燃氣輪機動態仿真模型研究[J].熱能動力工程,2001,16(5):523-526.
[5]夏 迪,王永泓.PG9197E 型燃氣輪機變工況計算模型的建立[J].熱能動力工程,2008(4):338-342.
[6]童萬軍,唐世建.基于流量法的齒輪傳動渦扇發動急動態建模[J].航空動力學報,2011,26(6):1377-1383.
[7]張 杰,張雪梅,沈 岑,等.基于Modelica/Dymola 的小型燃氣輪機建模與仿真[J].機電工程,2013,30(4):476-479.
[8]黃開明,劉 杰.基于無迭代法的航空發動機的實時模型[J].航空發動機,2004,30(2):35-38.
[9]UZOLO.A new high-fidelity transientaero thermalmodel for real-timesimulationsof the T700 helicopter turboshaftengine[J].ThermalScienceand Technology,2011,31(1):37-44.
[10]韓曉光,曲文浩,董 瑜,等.基于Simulink 的燃氣輪機動態仿真的模型[J].航空發動機,2010,36(3):20-25.

