焊接機器人運動學分析及軌跡規劃研究

劉 鵬，宋 濤，贠 超，高志慧

（北京航空航天大學 機械工程及自動化學院，北京 100191）

0 引 言

隨著工業自動化技術的提高，焊接機器人技術日趨成熟，現已大量應用到工業生產中。為實現對石化容器、梁構等大型焊件的自動焊接，筆者所在的課題組與北京中電華強焊接工程技術有限公司聯合研制了7 自由度大型焊接機器人“中電一號”。

為了保證焊接質量，弧焊機器人作業過程中，不僅對末端執行器（焊絲）的位姿、速度及加速度有很高的要求，而且要求運動軌跡為連續平滑的曲線。因此研究者需要建立機器人運動模型，并對其運動軌跡進行規劃，從而滿足焊接工作的要求。

本研究運用D-H 坐標系理論，分析該機器人的運動學問題[1]；并在運動學分析的基礎上，在關節空間采用三次多項式函數插值法，研究機器人軌跡規劃的問題；最后在Matlab7.8 平臺上，運用機器人工具箱[2]進行仿真，以驗證軌跡規劃的合理性。

1 運動學分析

1.1 機器人結構分析及D-H 坐標系建立

“中電一號”是個7 自由度關節式機器人，其結構圖如圖1 所示。該機器人由腰部、大臂、小臂和腕部等部分組成，所有關節均為轉動關節。

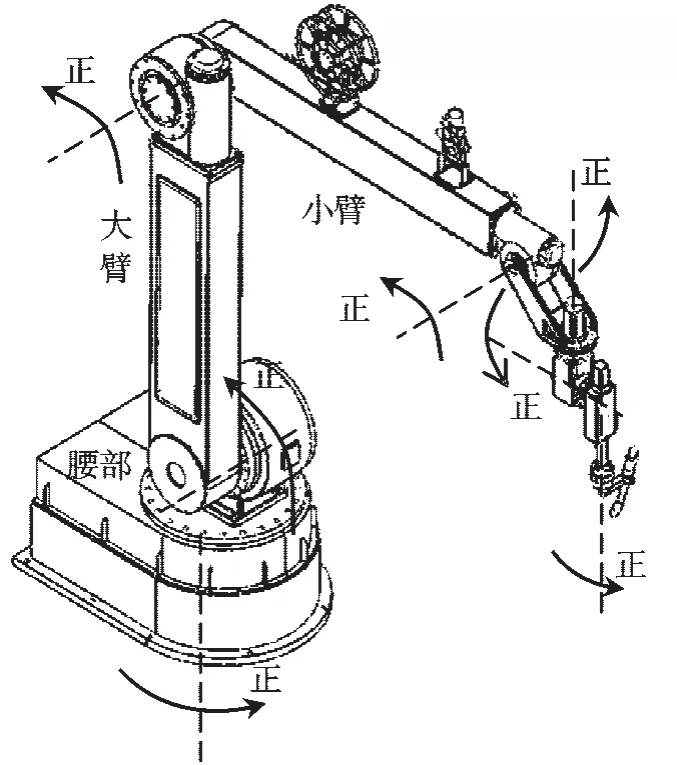
圖1 7 自由度機器人結構圖

從理論上來說，該7 自由度機器人為冗余度機器人。但是實際上，機器人的第7 關節僅是為了滿足焊接工藝需要，使焊槍在焊接過程中保持轉動，不對機器人末端的運動軌跡產生影響。因此，研究者在進行運動學分析時，只需建立前6 個關節的運動學模型。

本研究按照D-H 方法建立其連桿坐標系，D-H 坐標系的建立如圖2 所示。

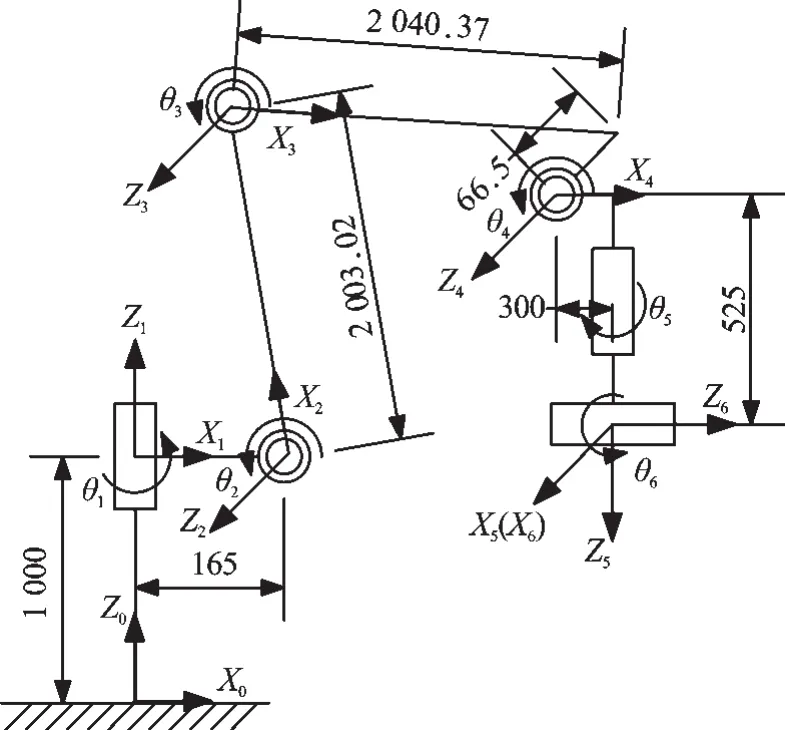
圖2 D-H 坐標系的建立

1.2 機器人正逆運動學分析

1.2.1 運動學正解

D-H 參數表如表1 所示。

根據連桿坐標系和D-H 參數表，機器人運動學方程可描述為：

式中：i-1iT—第i 個連桿坐標系相對于第i-1 個連桿坐標系的齊次變換矩陣。

且有：

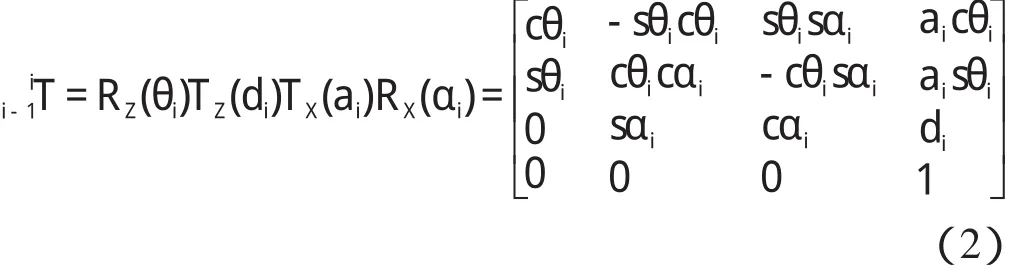
式中：cθi=cosθi，sθi=sinθi，cαi=cosαi，sαi=sinαi(i=0,1…6)。

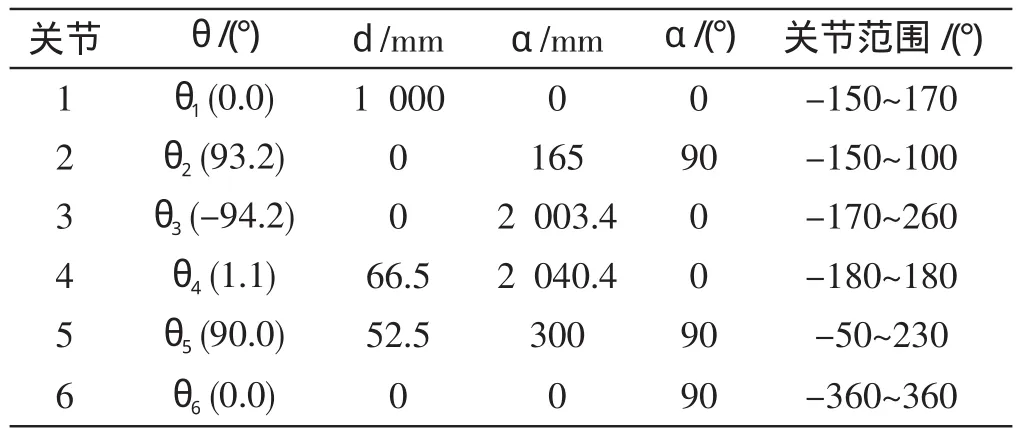
表1 D-H 參數表

將表1 中的連桿參數代入到式（1，2）中，得到機器人末端相對于基坐標系的位姿矩陣60Τ 。同時，末端在基座標系下的位姿亦可表示為：

式中：

1.2.2 運動學逆解

機器人逆運動學求解一般有兩種方法：封閉解法和數值解法[3]。封閉解法計算速度快，效率高，便于實時控制；數值解法是一種迭代法，不能求出所有的解。對于本研究設計的焊接機器人，由圖2 可以看出，其第2、3、4 關節軸相互平行，在結構上滿足Pieper 準則[4]，可以采用封閉解法。因此，本研究采用封閉解法來求解該逆運動學問題，則：

（1）求解 θ1。

在式（3）兩端同乘以01T-1，式（4）左邊第2 行第4 列元素為常數，將等式對應元素等同起來，可得：

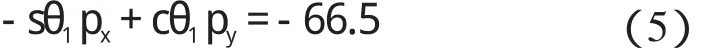
由三角代換可得：

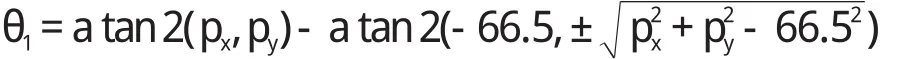
其中，正、負號對應的兩個解對應著θ1的兩個可能。

（2）求解 θ5。

在確定θ1的一個解之后，再觀察方程式（4）兩端第2 行前3 個元素，聯立等式，可求得：

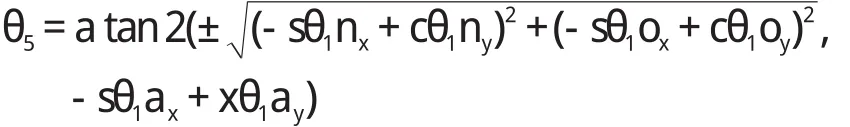
（3）求解 θ6。

令等式（4）兩端第2 行第1 列及第2 行第2 列元素對應相等，則有：

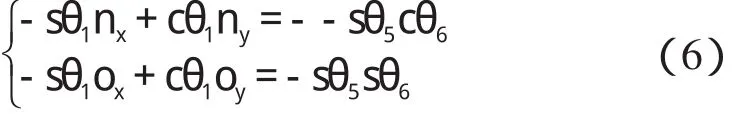
如果 sθ5≠ 0，則可解得：

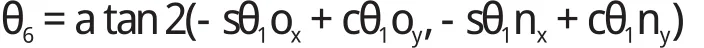
（4）求解 θ2。

令式（4）左右兩邊第1 行第3 列、第3 行第3 列元素對應相等，則有：

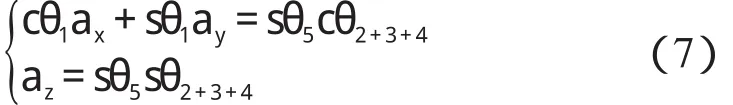
若 sθ5≠ 0，可解得：

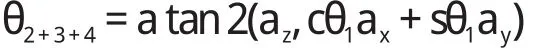
結合式（3），可得下列關系式：

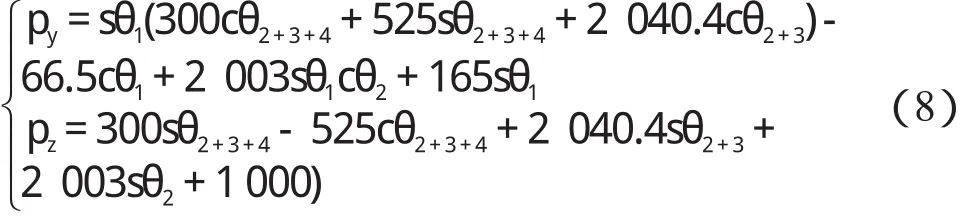
若 sθ5≠ 0，則令：

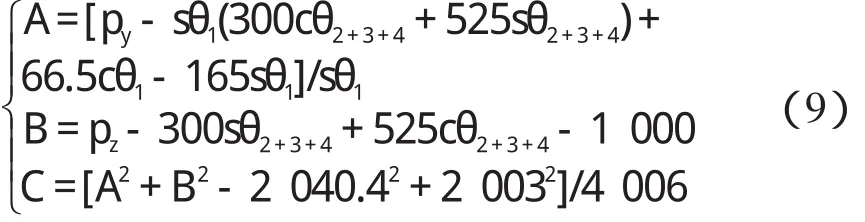
通過上式可解得：

（5）求解 θ3。

結合式（8，9），有：

進而可解得：

（6）求解 θ4。

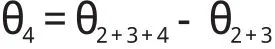
至此，6 個關節變量的逆解均已求得。θ1、θ2 以及θ5有兩個解，而θ3、θ4 和θ6 均只有一個解。因此滿足Pieper 準則的機器人最多有8 組解，但受關節轉動范圍的限制，某些解是偽解，不可實現[5]。

1.3 雅克比求解

焊接速度的均勻與否，直接關系著焊接質量的好壞[6]。因此，本研究必須通過雅克比對機器人進行速度的規劃。對于n 個關節的機器人，雅可比矩陣是6 ×n 矩陣，前3 行代表對夾手線速度v 的傳遞比，后3行代表對夾手角速度ω的傳遞比，即：

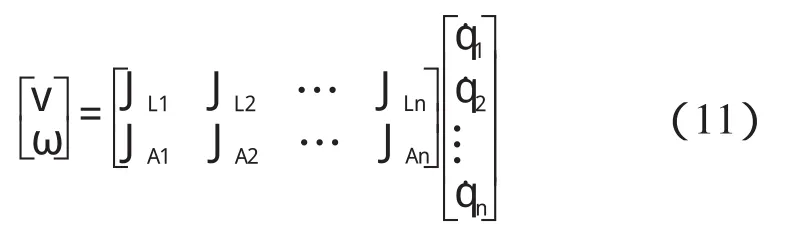
式中：n=6；雅克比矩陣—6 ×6 方陣；JLi，JAi—關節i 的單位關節速度引起夾手線速度和角速度。

本研究采用微分變換法求解雅克比矩陣。

因為中電一號各個關節為轉動關節，對于任意的關節i，連桿i 相對于連桿i-1 繞坐標系{}i 的zi 軸所作微分運動dθi，其微分運動矢量為：

由微分變換公式[7]，可解得夾手相應的微分運動矢量為：

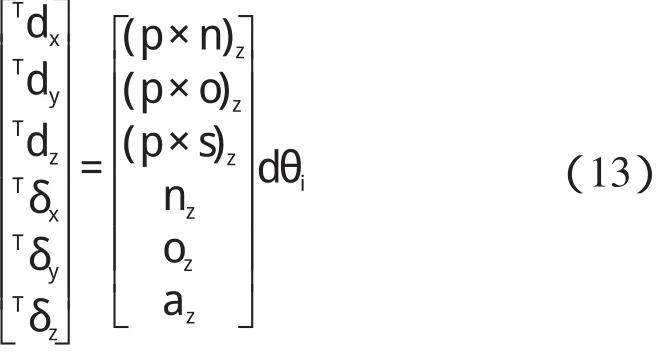
因此，可得雅克比矩陣J(q)的第i 列如下：

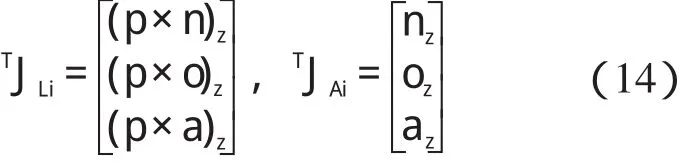
式（12～14）中：i=1,2…6；n,o,a,p—niT 的4 個列矢量。

受篇幅所限，對于雅克比矩陣各元素的具體數值，本研究不再給以表述。下文將在機器人運動學分析的基礎上，對其軌跡規劃進行研究。

2 軌跡規劃

關節空間的軌跡規劃具有計算簡單、不發生機構奇異性等特點[8]。關節空間的軌跡規劃有拋物線過渡線性插值、三次多項式插值、五次多項式插值及B 樣條插值法[9]。綜合考慮系統的穩定性及控制的實時性，本研究在三次多項式插值法的基礎上，在關節空間構造了過路徑點的三次多項運動路徑。該算法簡單、計算量小，且具有較高的控制精度，結合研究課題需要，本研究采用該算法進行關節空間軌跡規劃的研究。

2.1 笛卡爾空間到關節空間轉化

假設笛卡爾空間有一連續軌跡被離散為n 個空間位姿節點序列{T}，其上任意兩個相鄰的節點的位姿可表示為Ti、Ti+1，速度可表示為[viωi]T和[vi+1ωi+1]T。

根據1.3.2 部分內容，可求得兩節點所對應的兩組關節角度為 Θi、Θi+1；由1.4 節部分的內容，可推導出：

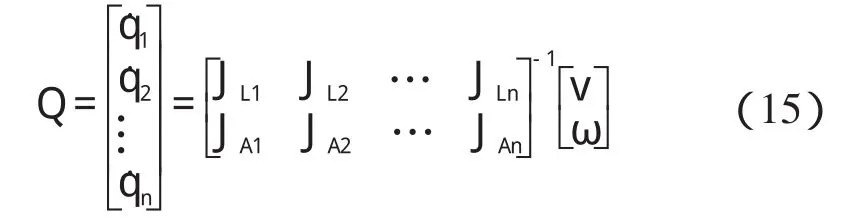
由式（15），從而求得其對應的關節速度為Qi和Qi+1。因此，對笛卡爾空間軌跡的規劃可間接轉化為對關節空間的軌跡規劃。

2.2 過路徑點的三次多項式插值

根據2.1 節中假設，在機械手運動過程中，需經過n 個空間位姿點。這n 個位姿點對應著關節空間的n組關節角度，也就意味著關節空間中各關節必過這n組關節角度。

對任意兩組相鄰的關節角度，本研究取其中某個關節進行分析，稱該關節前一個關節角度θi為起始點θ0，則后一個關節角度θi+1為終止點θf。該段運動軌跡的描述，可用起始點關節角度與終止點關節角度的一個平滑插值函數θ(t)來表示，θ(t)在t0=0 時刻的值是θ0，在終端時刻tf的值是終止關節角度θf。

為了實現單個關節的平穩運動，軌跡函數θ(t)至少需要滿足4 個約束條件。其中，兩個約束條件是起始點和終止點對應的關節角度：

為了滿足關節速度的連續性要求，在起始點和終止點的關節速度須滿足：

設三次多項式的表達式為：

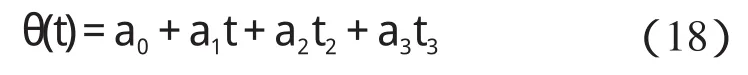
則結合式（16，17）可以求得三次多項式的系數如下式所示：

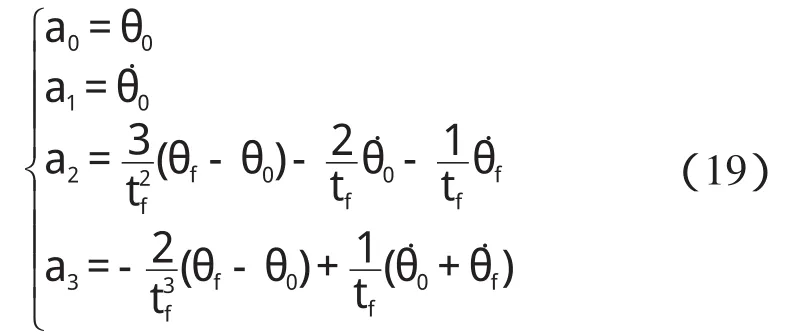
式中：θ0，θf，θ˙0，θ˙f—起始點和終止點的角度和角速度。

關于它們的求解方式，2.1 節中已闡述，不再贅述。

3 仿真驗證

本研究以Matlab7.8 為實驗平臺，運用機器人工具箱，對機器人運動學、軌跡規劃進行仿真分析[10]。

3.1 運動學建模

筆者運用機器人工具箱，結合D-H 參數，編寫相關代碼，以建立機器人模型：

3.2 運動學仿真

本研究假設機器人初始關節角度為q0=[0 0 0 0 0 0]，經歷2 s 運動到N（2.386，-0.066，2.431）時的關節角度為qn=[0 1.625-1.644 0.019 1.57 0]。

由運動學方程，可求得機器人末端初始位姿矩陣為：

機器人末端終止位姿矩陣為：

仿真中機器人將平穩地從初始位姿運動到終止位姿。機器人末端運動軌跡如圖3 所示。

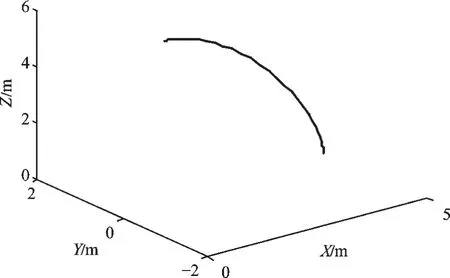
圖3 機器人末端運動軌跡

通過仿真，可以觀察到機器人各關節運動平穩，驗證了連桿參數設計的合理性和正解算法的正確性。

3.3 關節空間軌跡規劃仿真

根據機器人末端軌跡，本研究通過運動學反解得出各關節位移，由逆雅克比求出關節速度。再利用三次多項式進行插值，分別計算出6 個關節各自對應的a0，a1，a2，a3，實現各個關節的軌跡規劃。

本研究以Robotics Toolbox 為工具，驗證關節空間三次多項式插值規劃的合理性。假設機器人為剛體，末端沒有負載，仿真時間為2 s，機器人各關節從q0=[0 0 0 0 0 0]，運動到 qn=[p i/6 pi/5 pi/4 pi/3 pi/2 pi/1]，各變量隨時間變化的曲線圖如圖4 所示。

從圖4 中可以看出，各個關節的速度及加速度曲線連續且平滑，對各關節既無剛性沖擊又無柔性沖擊，故基本能夠滿足控制要求。同時也證明了機器人各連桿參數設計的合理性，以及基于關節空間的軌跡規劃方法的可行性。該技術目前已應用于機器人點焊、角焊作業中，實際使用效果較好。

4 結束語

本研究運用D-H 坐標系理論，研究了“中電一號”焊接機器人的運動學問題，并在運動學分析的基礎上，采用過路徑點的三次多項式函數插值法，實現了機器人在關節空間的軌跡規劃。

在Matlab7.8 平臺上，本研究建立了機器人運動學模型，對機器人運動學問題和關節空間軌跡規劃進行仿真驗證。仿真結果表明，機器人連桿參數設計合理、運動學模型建立正確，同時也驗證了基于關節空間的三次多項式函數插值算法的軌跡規劃方法合理可行，為機器人動力學及焊接機器人今后在馬鞍面多層多道焊接的研究打下了基礎。

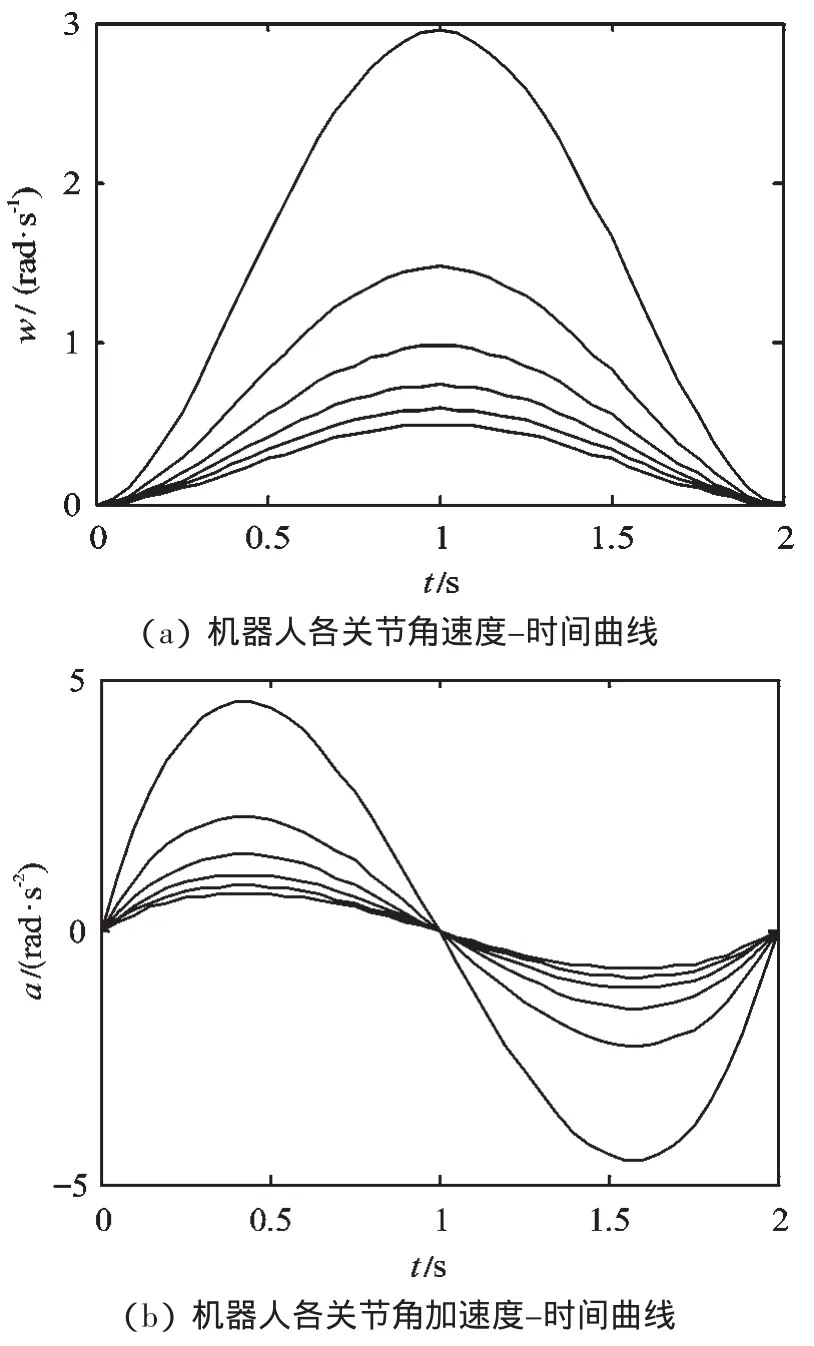
圖4 各變量隨時間變化的曲線圖

（References）：

[1]劉松國.六自由度串聯機器人運動優化與軌跡跟蹤控制研究[D].杭州：浙江大學流體傳動及控制國家重點實驗室，2009.

[2]謝 斌，蔡自興.基于Matlab Robotics Toolbox 的機器人學仿真實驗教學[J].計算機教育，2010（19）：140-143.

[3]熊有倫.機器人學[M].北京：機械工業出版社，1993.

[4]呂世增，張大衛，劉海年.基于吳方法的6R 機器人逆運動學旋量方程求解[J].機械工程學報，2010，46（17）：35-41.

[5]王 偉，謝明紅，周國義.6-DOF 工業機器人逆解優化及其工作空間的研究[J].機械與電子，2011（1）：57-60.

[6]毛志偉，李舒揚，葛文韜，等.移動焊接機器人大折角角焊縫跟蹤及工藝[J].焊接學報，2011，32（2）：33-36.

[7]蔡自興.機器入學[M].北京：清華大學出版社，2000.

[8]KUBOTA N，ARAKAWA T.Trajectory generation for redun?dantmanipulator using virus evolutionary genetic algorithm.[C]//Robotics and Automation，1997-Proceedings，IEEE In?ternational Conference on Albuquerque，USA：IEEE，1997：205-210.

[9]馮曉波.機器人準確制孔技術研究[D].杭州：浙江大學機械工程學系，2011.

[10]程永倫，朱世強，羅利佳，等.基于Matlab 的QJ-6R 焊接機器人運動學分析及仿真[J].機電工程，2007，24（11）：107-110.