彈性多質點共軸運動系統的控制算法研究*

楊海強，張得禮，安魯陵

（南京航空航天大學 機電學院，江蘇 南京 210016）

0 引 言

許多工業機械傳動系統（例如凹版印刷長軸驅動、紡紗機械中的羅拉傳動、全電型注塑機等設備）中大量使用的滾珠絲杠傳動、風力發電變槳傳動等，都會由于傳動系統的剛性不足而產生速度波動問題。針對彈性傳動系統的研究與速度波動控制，國內外專家學者已經做了大量的工作。Krzyszt of Szabat 等人[1]將卡爾曼濾波器應用于彈性連接的高性能傳動系統。Jaroslaw Guzinski 等人[2]采用速度和轉矩觀測器對高速列車的彈性傳動系統進行了控制。A.Hace 等人[3]對輸送帶彈性傳動系統的速度波動進行了控制。伍建國等人[4]基于Riccati 傳遞矩陣法建立了內圓磨床傳動系統的動力學模型。余丹萍等人[5]建立了CRH3 動車組牽引傳動系統仿真模型并對其直接轉矩控制方法的有效性進行了驗證。緱春芳[6]建立了風力發電機傳動系統模型并對齒輪部件進行了模態分析。

目前，許多彈性傳動系統都被簡化為兩質點系統，因此很多速度波動控制算法都是基于簡化后的二質量體傳動系統模型。

本研究在兩質點系統模型的基礎上，考慮更為復雜的三質點機械傳動系統模型。筆者采用基于模型控制的算法思想，在只用一個編碼器的情況下對三質量體系統的速度進行控制，達到很好的控制效果，為開環情況下解決復雜傳動系統速度波動問題提供有效的控制方法。

1 系統描述

三質點共軸彈性傳動系統模型結構如圖1 所示。

圖1 系統結構示意圖

圖1 中，3 塊大小不一的圓柱形質量體分別通過中心軸固定在立式支撐架上，并且3 個質量體的中心軸線處在一條水平線上。質量體從左數起：第1 塊和第2塊、第2 塊和第3 塊之間通過具有一定柔性的彈簧連接（彈簧的柔性和彈性可足以帶動軸和質量體的運動）。第1 塊質量體的左端直接與直流電機（帶減速器）連接，電機轉動則可以驅動3 塊質量體轉動。

由于彈簧柔性較大，電機、減速器和第1 塊質量體可以看成剛性連接。當電機開始運轉，由于彈簧的柔性作用，第2、第3 個質量塊需要經過很長時間的振動才能漸漸平穩，以相對穩定的速度運轉。

2 系統建模

2.1 機械部分建模

根據系統機械傳動特性，本研究對機械部分進行數學建模。建模時對系統進行如下簡化：

①把電機轉子、減速器、質量體1 看成一個整體進行轉動慣量的計算；②忽略質量體與支座之間的摩擦力。

機械部分動力學方程可表示為：

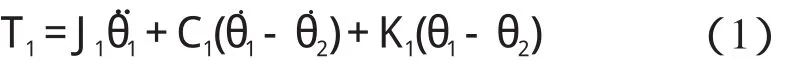
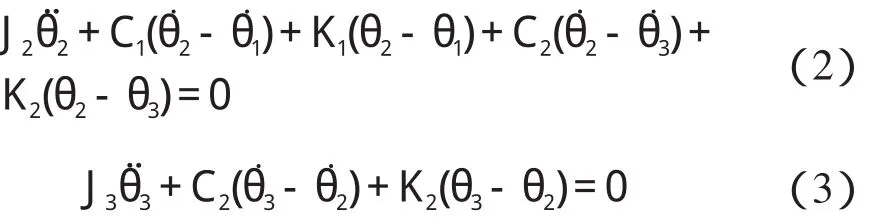
式中：T1—減速器輸出的扭矩；J1—電機+減速器+聯軸器+質量塊1 的等效到質量體1 軸上的轉動慣量；J2—質量塊2 軸上的轉動慣量；J3—質量塊3 軸上的轉動慣量；θ1—質量塊1 的角位移；θ2—質量塊2 的角位移；θ3—質量塊3 的角位移；C1，C2—彈簧阻尼系數，C1=C2=Cs；K1，K2—彈簧扭轉剛度系數，K1=K2=Ks。

2.2 直流電機部分建模

根據直流電動機電樞回路電壓平衡方程式和電機軸上的轉矩平衡方程式[7-8]，建立直流電機數學模型：

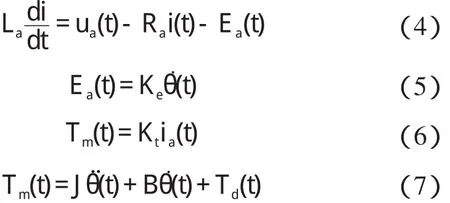
式中：La—電樞電感，ua—電樞電壓，i—電樞電流，Ea—反電動勢，Ra—電樞電阻，Ke—反電動勢系數，Kt—電機電磁轉矩系數，Tm—電機電磁轉矩，Td—電機負載轉矩，θ—電機轉子角位移，B—等效在電動機軸上的阻尼系數，J—電機轉子轉動慣量。

2.3 系統傳遞函數

本研究要實現無刷直流電機高精度和高動態性能的控制，不僅要控制電機轉速，同時還要控制速度的變化率也就是加速度。由直流電機的運動方程可知，加速度與電機轉矩成正比，而轉矩又與電動機的電流成正比。因而需要同時對電動機的速度和電流進行控制。為了實現高動態性能的速度控制系統，無刷直流電機采用轉速、電流雙閉環的控制模式。設直流電機速度環控制器傳遞函數為G(s)，由式（1～7）可以得到系統傳遞函數。在該系統模型中，系統輸入為質量體3 目標角速度θ˙i，輸出為質量體3 的實際角速度 θ˙3。

3 控制算法

3.1 系統模型的簡化

一般無刷直流電機的電氣時間常數遠小于其機電時間常數，因此電流環的動態響應性能遠大于速度環的動態響應性能，也就是電流的變化要比速度的變化快得多。而電機反電動勢與轉速成正比，因此在直流電機有合適的電流負反饋條件下，電機反電動勢對電流環的影響很小，可以忽略。本研究忽略電機電感La以及電機轉子阻尼系數B 的影響，簡化電機部分傳遞函數[9]。

簡化后系統傳遞函數可表示為如圖2 所示的框圖。

圖2 簡化后系統傳遞函數框圖

3.2 質量體3 轉速閉環控制方式

對質量體3 轉速w3 的控制是通過調節質量體2 的轉速w2實現的，而質量體2 的轉速是通過控制質量體1 的轉速w1 來進行調節。

本研究把質量體2 和質量體3 看成一個整體子系統，要使系統穩定，質量體2 和質量體3 必須以相同的速度進行運轉。本研究把質量體2 和質量體3 的速度差看作是子系統的輸出量，即質量體3 需要補償的速度量，設為Δw23。本研究把Δw23乘以比例系數k，與質量體2 的轉速相加，得到新的質量體2 的轉速w′2，w′2中包含了質量體3 所需補償的速度量。再用PI 控制器調節質量體1 與質量體2 的速度差Δw12，補償電機給定轉速，達到間接調節質量體3 的輸出轉速的目的。

閉環控制理論框圖如圖3 所示。

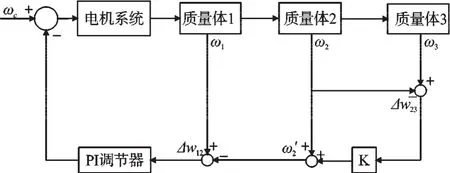
圖3 閉環控制理論框圖

3.3 基于模型算法的質量體3 轉速開環控制

在很多工業自動化控制環境下，在被控設備的末端執行器往往難以安裝測速傳感器，上述的全閉環控制很難實現。基于模型算法的思想就在于避免在控制回路中使用傳感器難以采集的末端執行器的速度信號（在圖1 所示的系統中可認為是質量體2 和3 的速度信號），而用簡化后的系統數學模型預估出質量體2的轉速wm2和質量體3 的轉速wm3，再用閉環控制的速度補償方式對速度進行控制。

控制理論框圖如圖4 所示。

4 實驗驗證

4.1 實驗系統的搭建

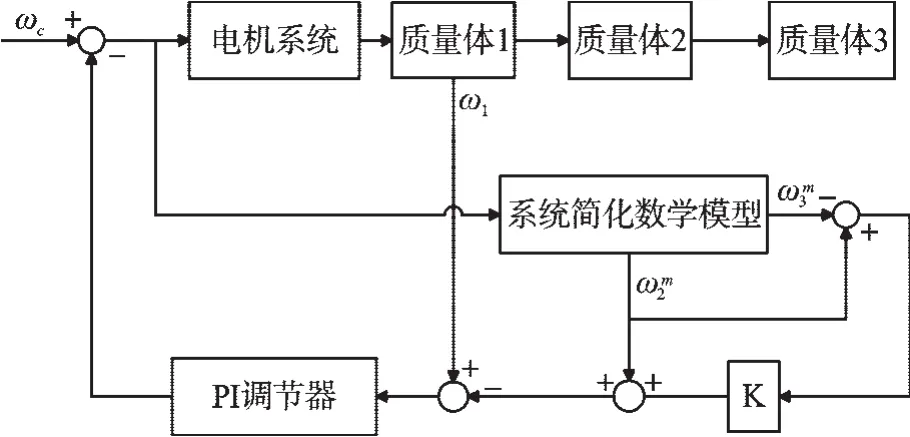
圖4 基于模型算法的控制理論框圖

為了驗證模型算法的控制效果，本研究搭建了三質量體彈性扭轉系統試驗臺，實物圖如圖5 所示。

實驗裝置由PLC、減速器、編碼器、轉動質量體、彈簧組成，其中PLC 部分使用了以下模塊：使用貝加萊X20 系列標準型CPU 作為PLC 系統的控制器；使用X20 系列的直流電機模塊MM2436 控制直流電機；使用X20 系列的編碼器模塊X20DC1976 接收編碼器的反饋信息。其中編碼器共有2 個，一個位于第一個質量體右端，用于測量質量體1 轉速，即電機轉速；一個位于第三塊質量體右端，用于測量第三塊質量體的轉速，該編碼器僅用于觀測控制效果。

圖5 試驗臺

4.2 實驗結果與分析

實驗過程中，系統輸入轉速恒定為2 500 °/s，通過質量體3 右端的編碼器觀測質量體3 的速度曲線。模型算法控制前質量體3 的響應速度曲線如圖6所示。此時，系統速度超調量為112%，調整時間為13.4 s。

模型算法控制后質量體3 速度曲線如圖7 所示。此時，系統超調量為4.2%，調整時間為1.2 s，質量體3的速度曲線已基本平滑。

實驗結果表明，模型算法對彈性三質點共軸運動系統的速度波動有很好的控制作用。

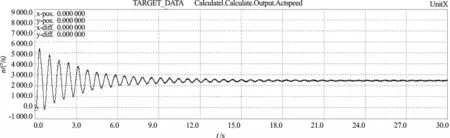
圖6 控制前質量體3 速度曲線

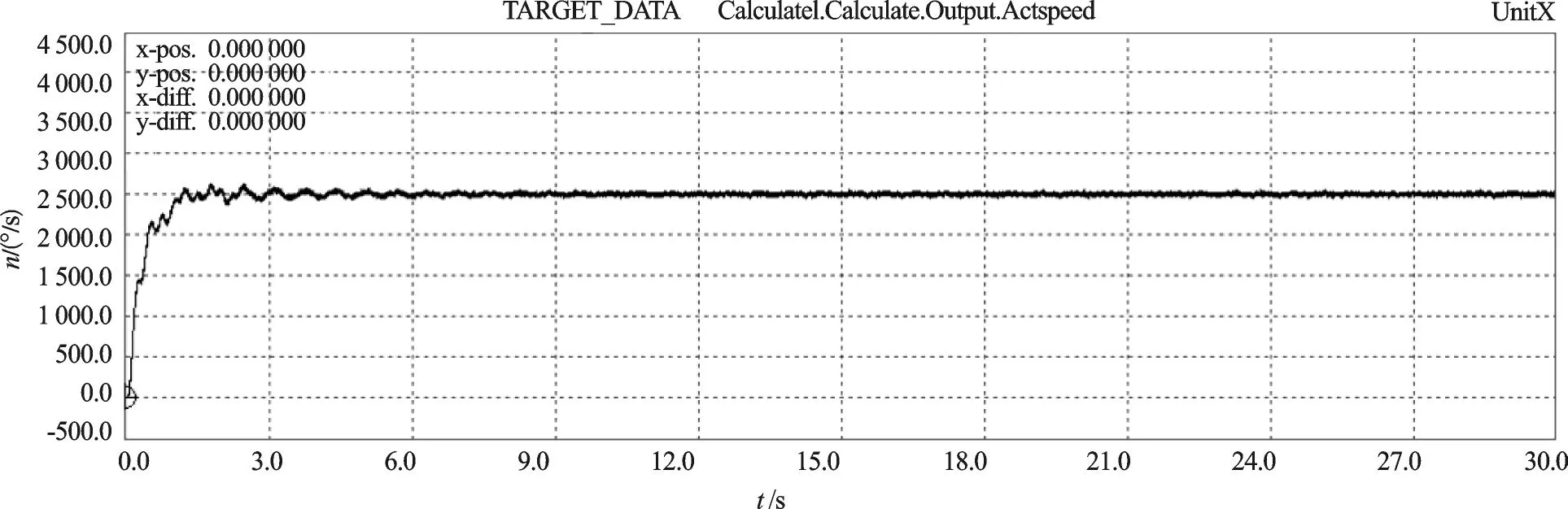
圖7 控制后質量體3 速度曲線

5 結束語

為了解決工業機械彈性傳動系統中出現的復雜速度波動問題，本研究提出了基于模型的彈性多質點共軸運動系統的控制算法，并且通過搭建三質點共軸運動系統試驗臺，對該算法的有效性進行了實驗驗證。實驗結果表明：在開環情況下，該算法可以對彈性傳動系統的速度波動問題進行有效的控制。

在下一階段，本研究將在實際工業控制場合進一步驗證算法的有效性。由于在實際工業控制環境下，被控設備的運行情況將更加復雜，在今后的研究中，研究者可能需要進一步改進控制算法，使之能應用于更為復雜多變的工業控制環境。

（References）：

[1]KRZYSZTOF S，TERESA O.Application of the Kalman fil?ters to the high-performance drive system with elastic cou?pling[J].IEEE Transactions on Industry Electronics，2012，59（11）：4226-4235.

[2]GUZINSKI J，ABU-RUB H，DIGUET M，etal.Speed and load torque observer application in high-speed train elec?tric drive[J].IEEE Transactions on Industry Electron?ics，2010，57（2）：565-574.

[3]HACE A，JEZERNIK K，SABANOVIC A.Improved design of VSS controller for a Linear belt-driven servomechanism[J].IEEE/ASME Transactions on M echatronics，2005，10（4）：385-390.

[4]伍建國，慶 鴻，毛海軍，等.Dynamic Characteristics of Transmission System for the Internal Grinder[J].Journal of Southeast University：English Edition，2002，18（4）：302-305.

[5]于丹萍，周 盛，江全元.CRH3 型動車組牽引傳動系統的直接轉矩控制研究[J].機電工程，2010，27（10）：62-67.

[6]緱春芳.風力發電機組傳動系統建模分析及齒輪的模態分析[J].現代機械，2010（1）：22-23.

[7]王志新，羅文廣.電機控制技術[M].北京：機械工業出版社，2010.

[8]潘丁丁.基于正交試驗的間歇傳動鏈動力學仿真研究[J].輕工機械，2011，29（1）：36-39.

[9]高鐘毓.機電控制工程[M].北京：清華大學出版社，2011.