靜電驅(qū)動裂紋微懸臂梁結(jié)構(gòu)振動特性分析

劉素娟，齊書浩，張文明

(上海交通大學(xué) 機械系統(tǒng)與振動國家重點實驗室，上海 200204)

微懸臂梁是MEMS器件中最典型的結(jié)構(gòu)之一，最早應(yīng)用于原子力顯微鏡中，被用來進行微小力的檢測和微觀表面成像等功能［1－2］。隨著 MEMS技術(shù)的發(fā)展，微懸臂梁作為一種新型檢測元件和傳感元件得到了越來越廣泛的應(yīng)用。

在微尺度下，靜電力存在著諸如吸合效應(yīng)、固有非線性及剛度軟化等非線性特性。許多學(xué)者在這些方面做了大量的研究。Sayanu等［3］基于集總模型推出兩端固支梁和懸臂梁的吸合電壓的表達式，利用等效剛度，研究了靜電激勵兩端固支梁和懸臂梁的吸合電壓。Slava等［4］充分考慮非線性靜電力、壓膜阻尼以及轉(zhuǎn)動慣量的影響，研究了靜電激勵微梁的吸合動力學(xué)。Fadi等［5］研究了靜電驅(qū)動共振傳感器的非線性共振和吸合效應(yīng)，從理論和實驗角度分析了主共振、超諧波共振次諧波共振和吸合現(xiàn)象。Zhang等［6］研究了參數(shù)激勵下共振質(zhì)量傳感器的非線性動力學(xué)特性，包括立方剛度和靜電剛度對諧振器動力學(xué)響應(yīng)的影響，研究發(fā)現(xiàn)，機電耦合產(chǎn)生的非線性因素對傳感器的穩(wěn)定性有一定的影響。正確預(yù)測擠壓膜阻尼對于MEMS器件設(shè)計是至關(guān)重要的，李普等［7］從彈性微梁振動方程和雷諾方程的耦合關(guān)系出發(fā)，提出了新的彈性懸臂梁擠壓模阻尼解析模型，結(jié)果表明，相對其它模型，該模型的計算精度有較明顯的提高。

無論是理論研究還是工程應(yīng)用，固體結(jié)構(gòu)中的裂紋仍然是一個基本問題。裂紋會出現(xiàn)在結(jié)構(gòu)元件中，由材料內(nèi)部初始缺陷或在其使用壽命期間由疲勞引起，導(dǎo)致結(jié)構(gòu)動力學(xué)特征的改變。很多學(xué)者在這方面進行了研究，并根據(jù)結(jié)構(gòu)振動特性的改變提出了損傷檢測的方法［8－9］。Fernandez-Saez 等［8］采用彈性旋轉(zhuǎn)彈簧模擬裂紋的作用，提出了使用影響函數(shù)法來計算裂紋Euler-Bernoulli梁的特征值問題的方法，并通過該方法得出裂紋Euler-Bernoulli梁彎曲振動的固有頻率近似解。Andreaus等［10］分析了諧波激勵下裂紋懸臂梁非線性響應(yīng)的特有特性，結(jié)果表明，在次諧波和超諧波激勵下，由于裂紋的存在，系統(tǒng)表現(xiàn)出的周期倍增和準脈沖行為特性，這些特性可用于結(jié)構(gòu)的損傷識別。劉文光等［11］采用復(fù)數(shù)阻尼理論，研究了裂紋位于懸臂梁根部并受橫向載荷時梁的結(jié)構(gòu)振動，使振動分析與疲勞裂紋擴展壽命估算同步進行，提出了一種含裂紋結(jié)構(gòu)的振動疲勞分析思路。Loutridis等［12］采用瞬時頻率研究了諧波激勵下裂紋懸臂梁的振動特性，提出了梁結(jié)構(gòu)中裂紋識別的一種新方法。

目前，在靜電驅(qū)動裂紋微器件的振動特性分析方面的研究較少［13－15］。Loya 等［13］基于非局部彈性理論建立了裂紋Euler-Bernoulli微納米梁模型，研究了裂紋位置、開裂程度及非局部效應(yīng)對簡支和兩端固定裂紋微納米梁的彎曲振動的影響。Ke等［14］基于Timoshenko梁理論研究了裂紋深度、裂紋位置、裂紋個數(shù)、材料特性、梁的細長比及邊界支撐條件對功能梯度材料含常開邊裂紋微梁的彎曲振動和彈性屈曲的影響。Hasheminejad 等［15］基于 Euler-Bernoulli梁理論，采用轉(zhuǎn)動彈簧模型研究了受表面效應(yīng)影響的裂紋納米梁的自由振動。以上研究主要集中在裂紋微納米梁的自由振動，而作為MEMS器件主要驅(qū)動方式之一的靜電驅(qū)動在微尺度下具有豐富的非線性特性，因此對靜電驅(qū)動裂紋微器件的振動特性進行分析具有重要的意義。

本文基于Euler-Bernoulli梁模型，采用無質(zhì)量彈性轉(zhuǎn)動彈簧模型模擬裂紋，考慮壓膜阻尼的影響，對靜電驅(qū)動裂紋微懸臂梁系統(tǒng)建立動力學(xué)模型，研究裂紋開裂程度、裂紋位置、激勵電壓、電極間隙以及壓膜阻尼對微懸臂梁固有頻率和振動特性的影響，以及裂紋對吸合電壓的影響。

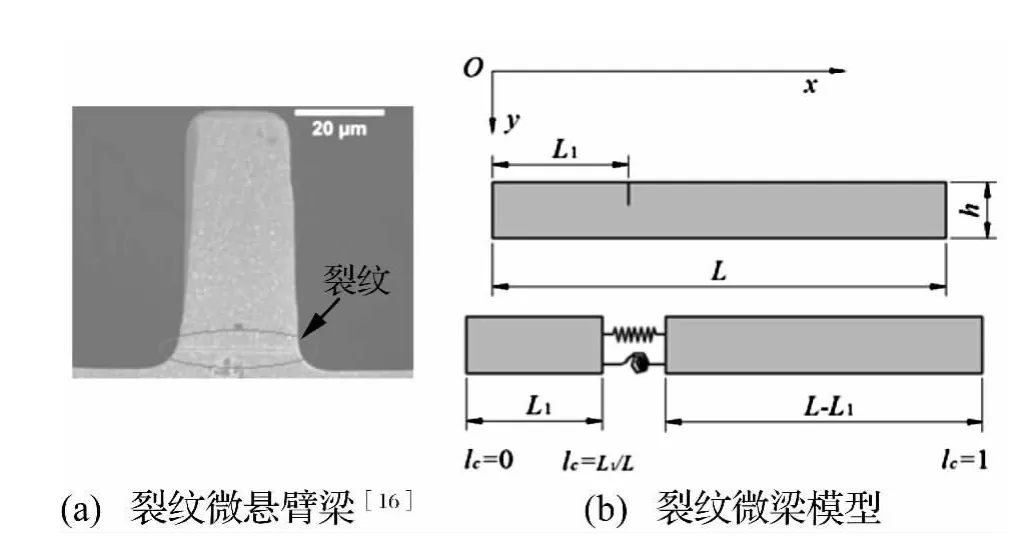
圖1 裂紋微懸臂梁及模型Fig.1 A cracked micro-cantilever beam［16］ and model

1 裂紋微梁結(jié)構(gòu)動力學(xué)建模與分析

1.1 耦合動力學(xué)模型

采用Euler-Bernoulli梁模型，靜電驅(qū)動梁的振動控制方程為:

式中:E為梁的彈性模量，I=bh3/12為截面慣性矩，b和h分別是梁的寬度和厚度，ρ和A分別是材料密度和截面面積;是靜電力產(chǎn)生的單位長度載荷［19］，Vp為直流偏置電壓，Vac為交流驅(qū)動電壓幅值，ωe為驅(qū)動電壓頻率，ε0=8.85 ×10－12C2·N－1·m－2為真空介電常數(shù)，εr為相對介電常數(shù)，d0為初始時刻微梁與固定電極之間的距離。考慮普通矩形板壓膜阻尼［19］，其中μ =1.86 ×10－5N·S/m2為動力粘度

引入無量綱變量

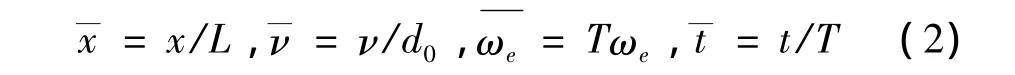
由此，可得微梁動力學(xué)方程的無量綱形式為:

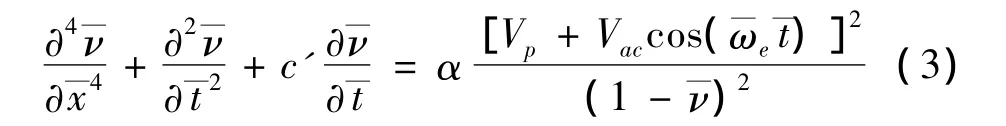
式中:α = ε0εrbL4/2dEI=6ε0εrL4/Eh3d，

0兩部分組成，即:

將式(4)代入式(3)右端項，按級數(shù)展開，并略去Δv—和Vac的高階項得到微梁振動的動力學(xué)方程為:

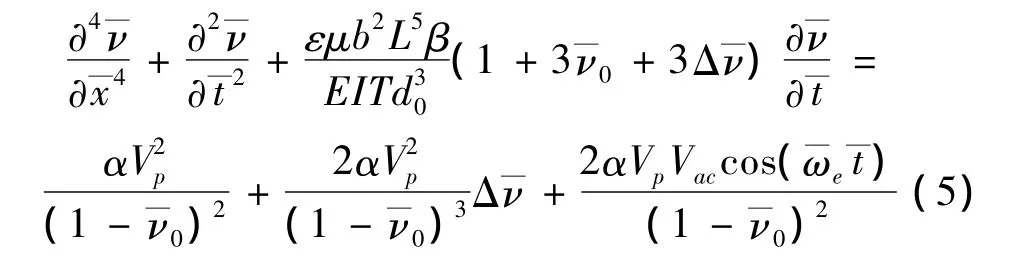
1.2 裂紋微梁自由振動分析

自由振動分析是討論微梁僅在直流偏置電壓Vp作用下的振動，微梁的靜態(tài)變形方程和動態(tài)振動方程分別為:

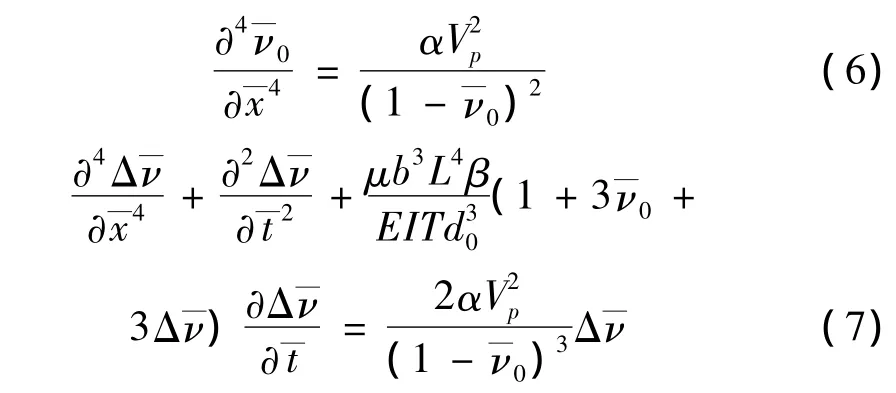
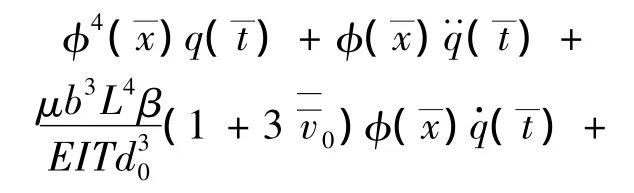
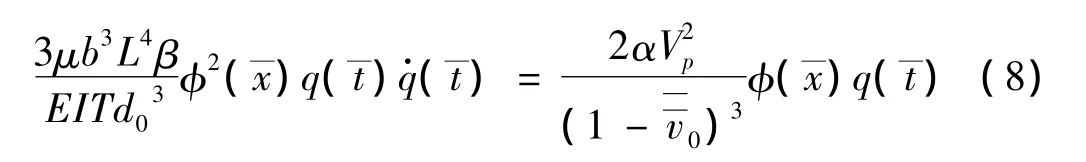
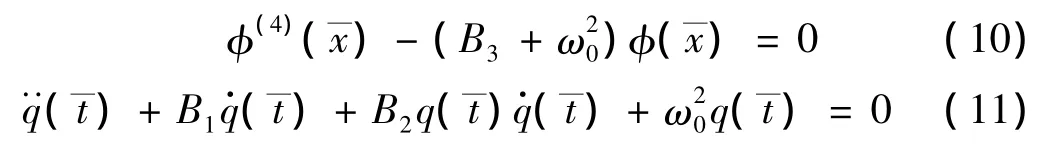
圖1(a)為裂紋微懸臂梁實例，圖1(b)為裂紋微梁模型，裂紋位于梁一端L1處，相對無量綱變量為lc=L1/L。模型中采用無質(zhì)量轉(zhuǎn)動彈簧模型模擬裂紋，該模型會引起位移一階導(dǎo)數(shù)不連續(xù)，且不連續(xù)度與位移二階導(dǎo)數(shù)成比例。自由彎曲振動情況下，相對轉(zhuǎn)動彈簧的轉(zhuǎn)角，縱向位移可忽略，因此，x=L1處轉(zhuǎn)動彈簧轉(zhuǎn)角的無量綱形式為［13］:

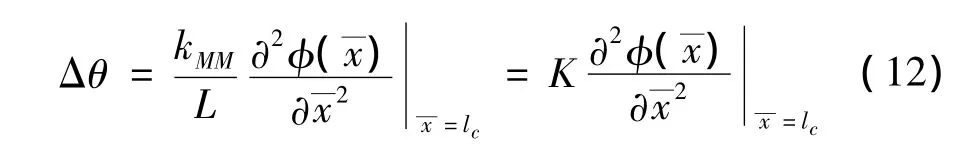
式中:kMM為彈性常數(shù)，表示裂紋開裂程度。

于是，裂紋梁的模態(tài)振動方程為:

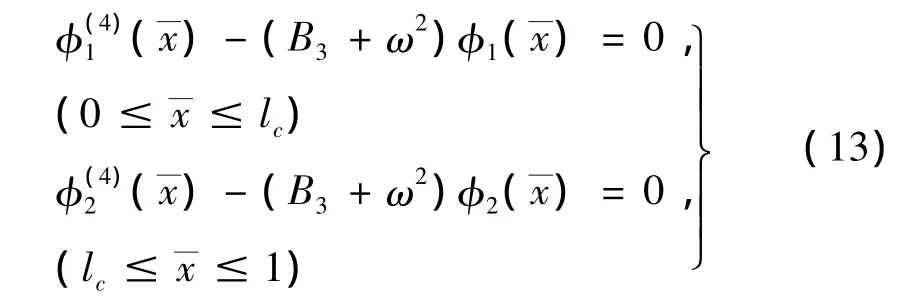
相應(yīng)方程的通解為:

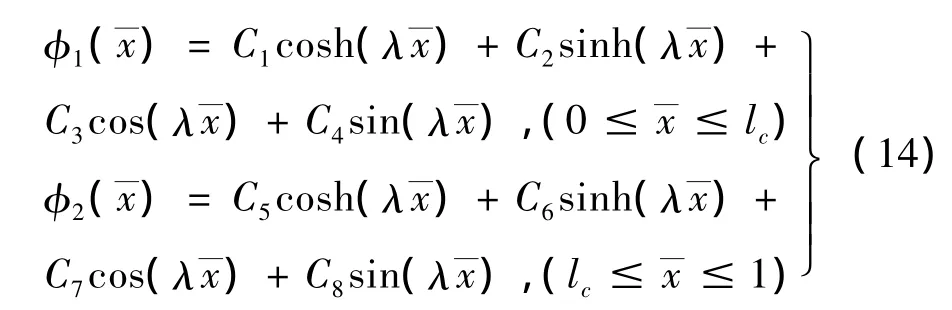
式中:λ4=(B3+);C1，C2，C3，C4，C5，C6，C7，C8為待定常數(shù)，由裂紋梁邊界條件及相容條件確定，即:

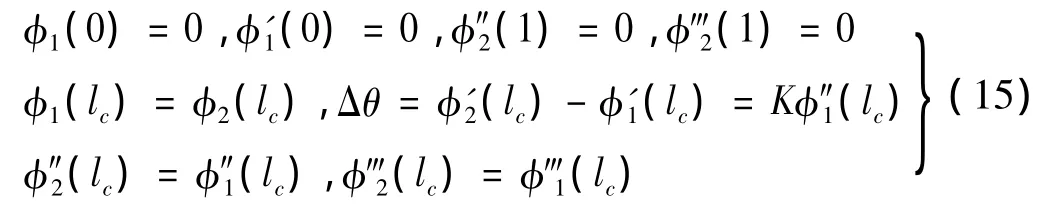
將式(15)代入方程(14)可導(dǎo)出一個線性系統(tǒng)方程組，它的行列式即系統(tǒng)特征方程，最終可確定系統(tǒng)的固有頻率。

1.3 裂紋微梁受迫振動分析

由微梁的振動方程(5)可知，微梁的受迫振動微分方程為:

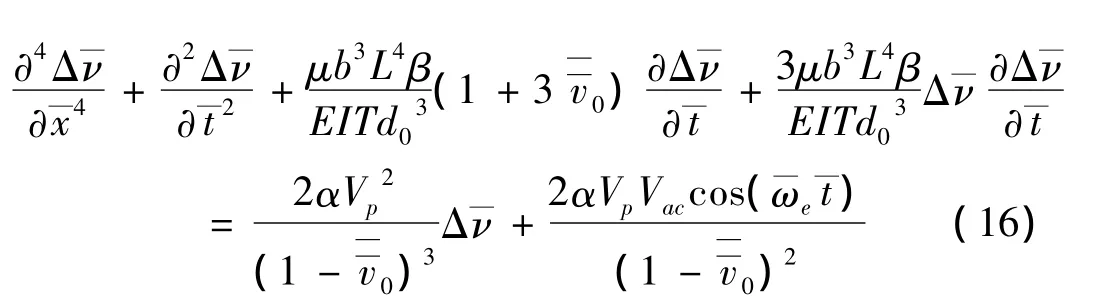
采用與自由振動分析相同的方法，得到微梁的振型方程與自由振動時相同，動態(tài)響應(yīng)方程為:

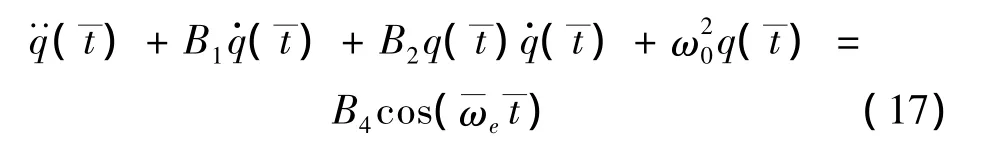
式中，B1、B2的表達式與式(9)中相同，B4=

1.4 靜電吸合效應(yīng)

吸合電壓可以表示為梁與固定電極之間間隙d0、梁的厚h和長度L的函數(shù)［17］，將轉(zhuǎn)動慣量 I=bh3/12代入函數(shù)，可得吸合電壓與梁剛度EI、間隙d0、梁的寬度b和長度L的關(guān)系為:

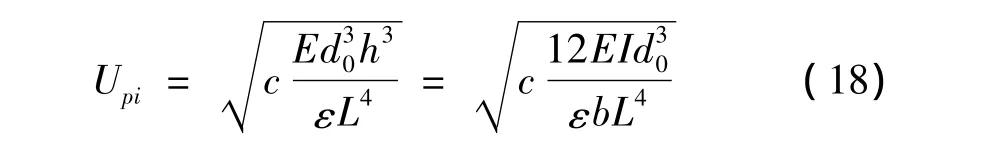
式中:ε為介電常數(shù)。

由此，可得裂紋梁的吸合電壓為:

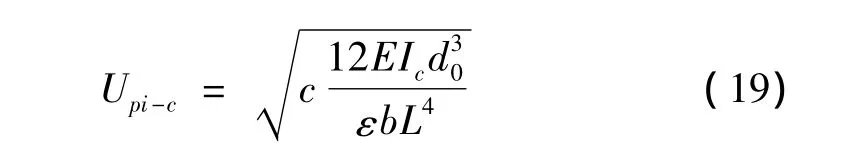
式中:EIc是裂紋梁的抗彎剛度;對于懸臂梁，常數(shù)c=0.28［17］。

對于裂紋位于L1，深度為a的梁，在任意x處梁的剛度為［18］:

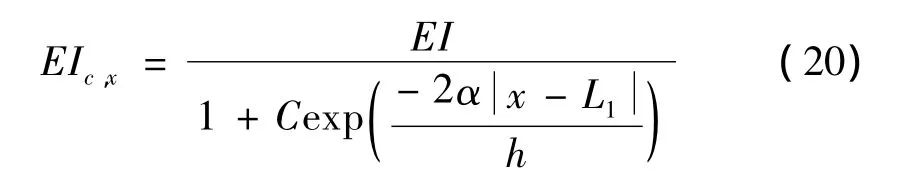
式中:C=(I－Ic)/Ic，Ic=b(h－a)3/12。Christides等［18］通過實驗得到常數(shù)α的值為0.667。

結(jié)合式(18)，(19)，(20)可得，正則化吸合電壓為:

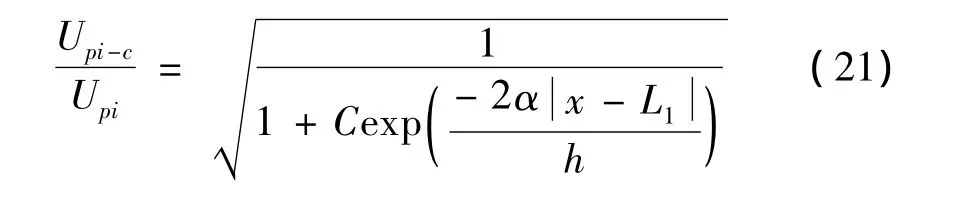
2 數(shù)值仿真及結(jié)果分析

本文中梁的材料為硅，梁的尺寸和材料參數(shù)如下:L=200 μm，h=4.5 μm，b=80 μm，E=190 GPa，ρ=2 500 kg/m3。定義梁的正則化固有頻率為ωc/ωn，其中ωc和ωn分別為裂紋梁和非裂紋梁的固有頻率。

2.1 自由振動分析

裂紋開裂程度和無量綱裂紋位置對梁在x－y方向上的前兩階正則化固有頻率的影響如圖2和圖3所示，圖中 ωc1/ωn1和 ωc2/ωn2分別為一階、二階正則化固有頻率。

圖 2 反映了裂紋位置 lc=0.25，0.5，0.75 時，梁的前兩階正則化固有頻率隨開裂程度的變化。由圖2(a)可知，當 lc=0.25時，ωc1/ωn1隨 K 的增加下降最為劇烈。由圖2(b)可知，當 lc=0.5 時，ωc2/ωn2下降最為劇烈;而當lc=0.25時，二階頻率變化最小。

圖 3 反映了裂紋開裂程度 K=0.5，1.0，1.5 時，梁的前兩階正則化固有頻率隨裂紋位置的變化。由圖3(a)可知，K越大，裂紋越靠近懸臂梁根部，一階固有頻率越小。由圖3(b)可知，當裂紋越靠近lc=0.22時，固有頻率變化越小，開裂程度對固有頻率的影響也越小;當裂紋越靠近lc=0.55時，固有頻率變化越大，開裂程度對固有頻率的影響也越大，lc=0.22和lc=0.55分別是第二節(jié)模態(tài)的節(jié)點和反節(jié)點。

由圖2～圖3知，裂紋位置和開裂程度對梁的固有頻率都有很大的影響。對于一階模態(tài)，隨著K增加以及l(fā)c的減小，固有頻率逐漸減小。對于高階模態(tài)，開裂程度對梁固有頻率的影響與裂紋位置離相應(yīng)模態(tài)節(jié)點和反節(jié)點的遠近程度有較大的關(guān)系。特別是，當裂紋位于模態(tài)節(jié)點時，固有頻率不隨開裂程度的變化而變化;當裂紋位于模態(tài)反節(jié)點時，固有頻率對開裂程度最敏感，受開裂程度的影響最大。而Hasheminejad等［15］的研究中也有相似的結(jié)論，即當裂紋位于相應(yīng)模態(tài)的振動節(jié)點時，開裂程度對系統(tǒng)自然頻率沒有影響。

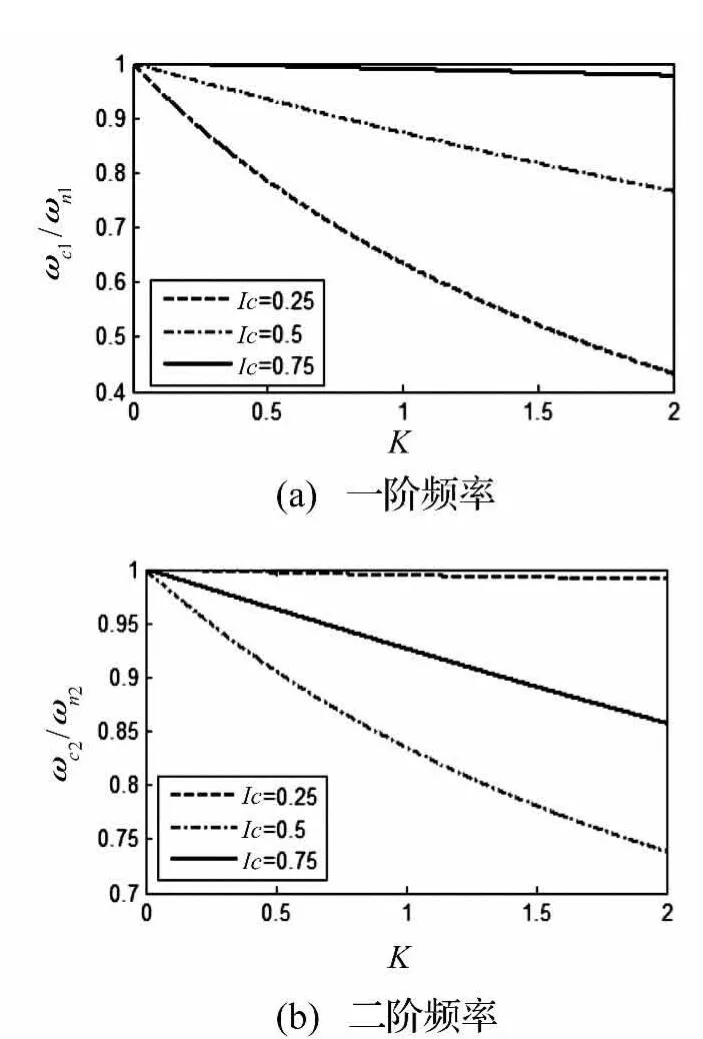
圖2 正則化固有頻率隨裂紋開裂程度變化圖(d0=3 μm，Vp=60 N)Fig.2 Normalized natural frequencies as a function of crack severity for selected crack positions(d0=3 μm，Vp=60 N)

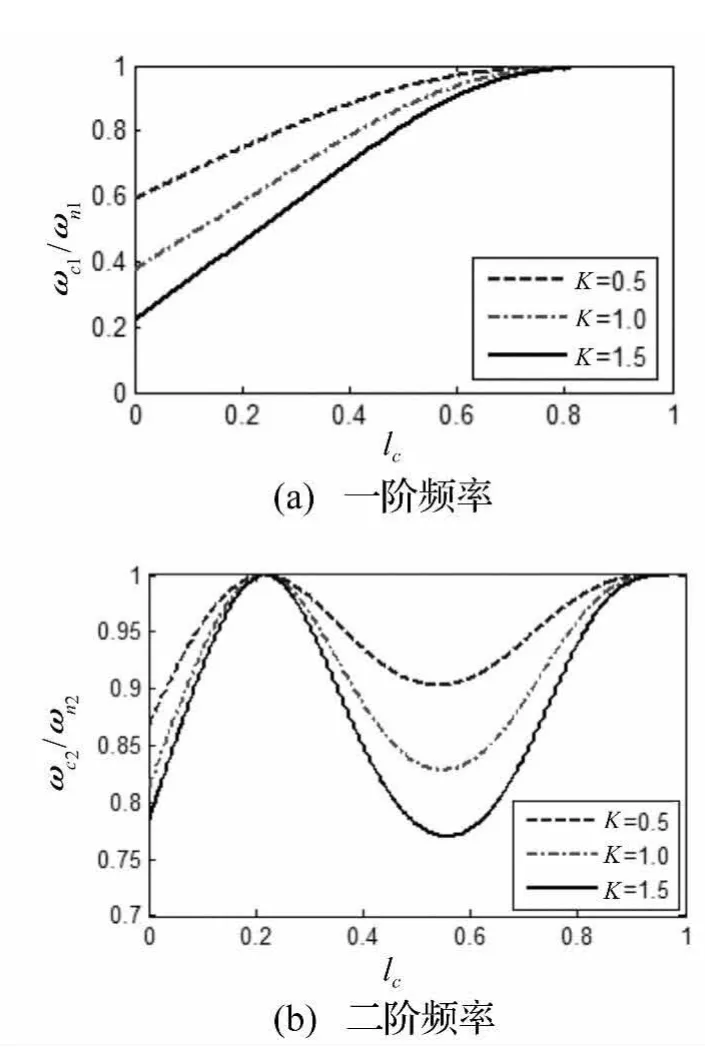
圖3 正則化固有頻率隨裂紋位置變化圖(d0=3 μm，Vp=60 N)Fig.3 Normalized natural frequencies as a function of crack position for selected crack severities(d0=3 μm，Vp=60 N)

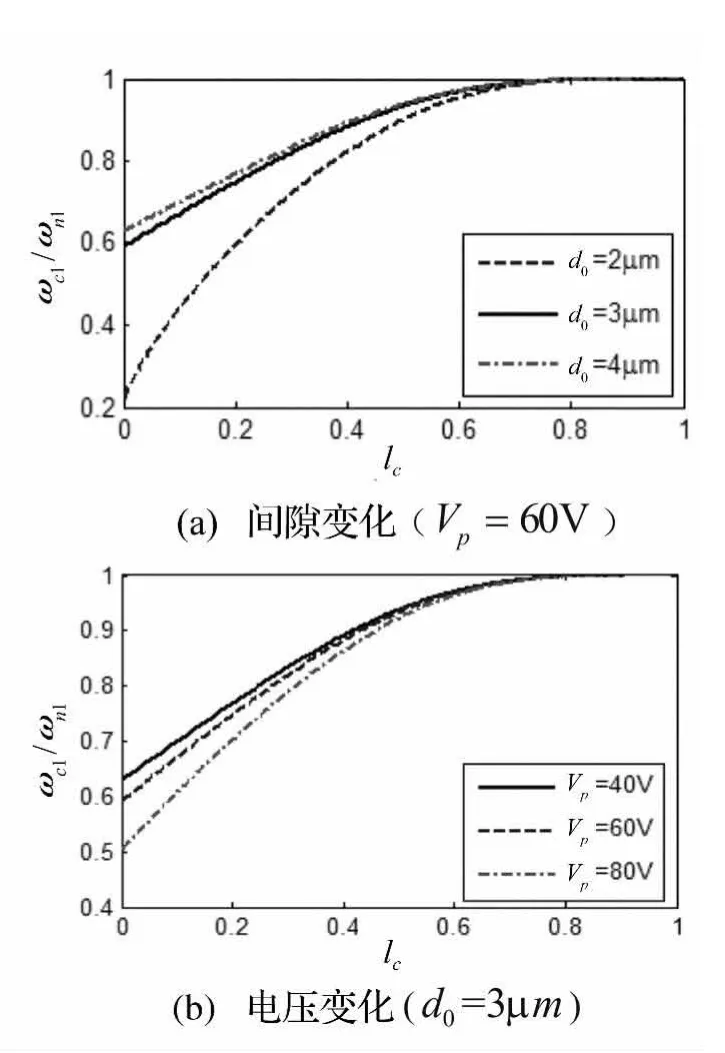
圖4 不同參數(shù)下正則化固有頻率隨裂紋位置變化圖(K=0.5)Fig.4 Normalized natural frequencies as a function of crack position for selected initial gaps and crack severity(K=0.5)

圖4為當K=0.5時，不同參數(shù)情況下正則化固有頻率隨裂紋位置變化圖。由圖4(a)可知，固有頻率隨懸臂梁與固定電極之間的間隙減小而減小，特別地，當d0=2 μm時，固有頻率明顯減小。由圖4(b)可知，隨著加載電壓的增加，固有頻率也將逐漸減小。

2.2 受迫振動分析

圖5為在裂紋位于不同位置時，微梁受迫振動幅值隨直流偏置電壓和交流電壓變化的響應(yīng)曲線。從圖中可以看出，當激勵電壓頻率與結(jié)構(gòu)固有頻率之比ωe/ω0→1時，系統(tǒng)的振動幅值達到最大，即出現(xiàn)共振現(xiàn)象;隨著直流偏置電壓和交流電壓幅值的增大，系統(tǒng)的振幅也隨之增大;在相同電壓情況下，裂紋越靠近懸臂梁根部，系統(tǒng)的振幅越大。

圖6(a)和(b)分別為在裂紋位于lc=0.2和lc=0.5時，無壓膜阻尼與不同壓膜阻尼時裂紋微梁振動幅值之比。從圖中可以看出，壓膜阻尼對系統(tǒng)振幅有著較大的影響。無壓膜阻尼時裂紋微梁振動幅值較大;隨著氣體動力粘度的逐漸增大，系統(tǒng)所受的壓膜阻尼力也逐漸增大，系統(tǒng)振幅逐漸減小，幅值比逐漸增大。從圖中還可以看出，在氣體動力粘度相同的情況下，裂紋越靠近懸臂梁根部，系統(tǒng)的振幅越大。

圖7為裂紋位于lc=0.5，不同裂紋深度時，正則化吸合電壓隨位置的變化曲線。由圖可見，裂紋越深吸合電壓越小。

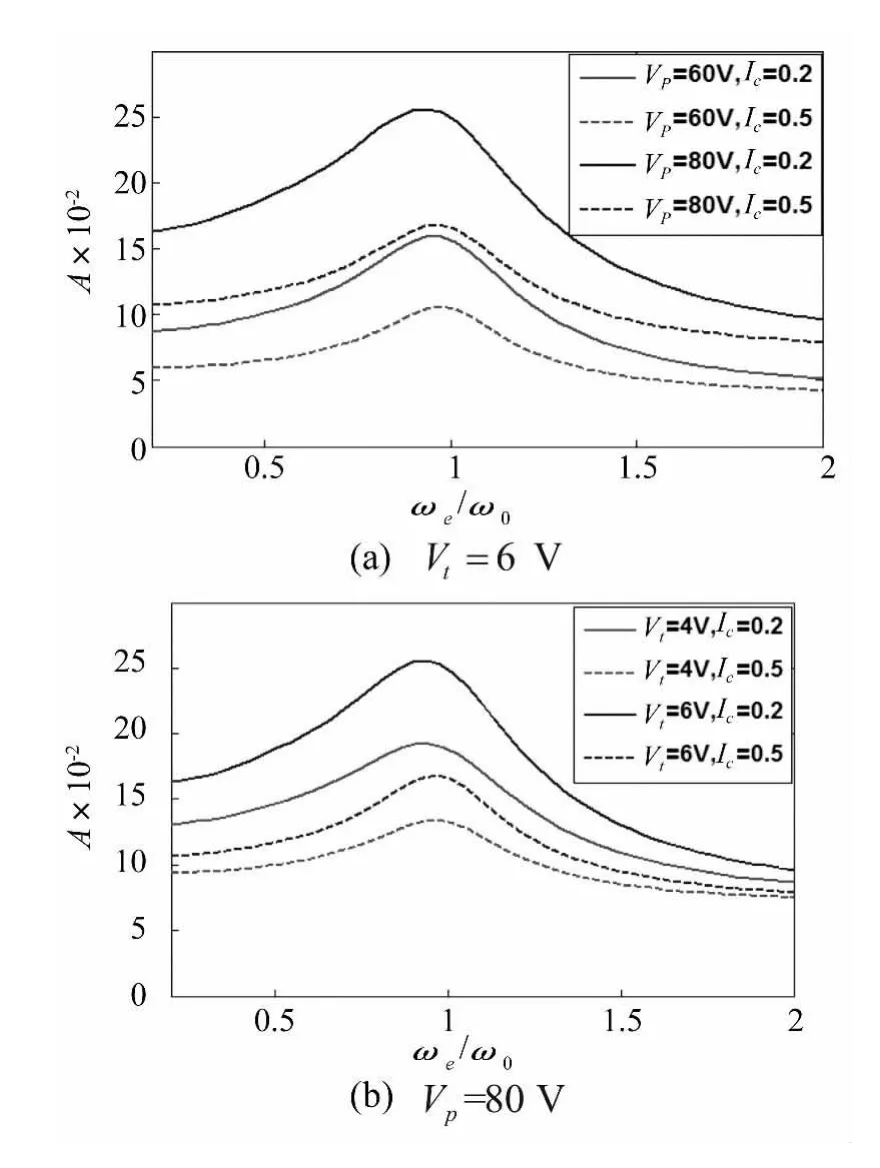
圖5 不同電壓下裂紋微梁的幅頻特性曲線(K=0.5)Fig.5 Frequency response curves of cracked microbeam for different voltages and selected crack positions(K=0.5)

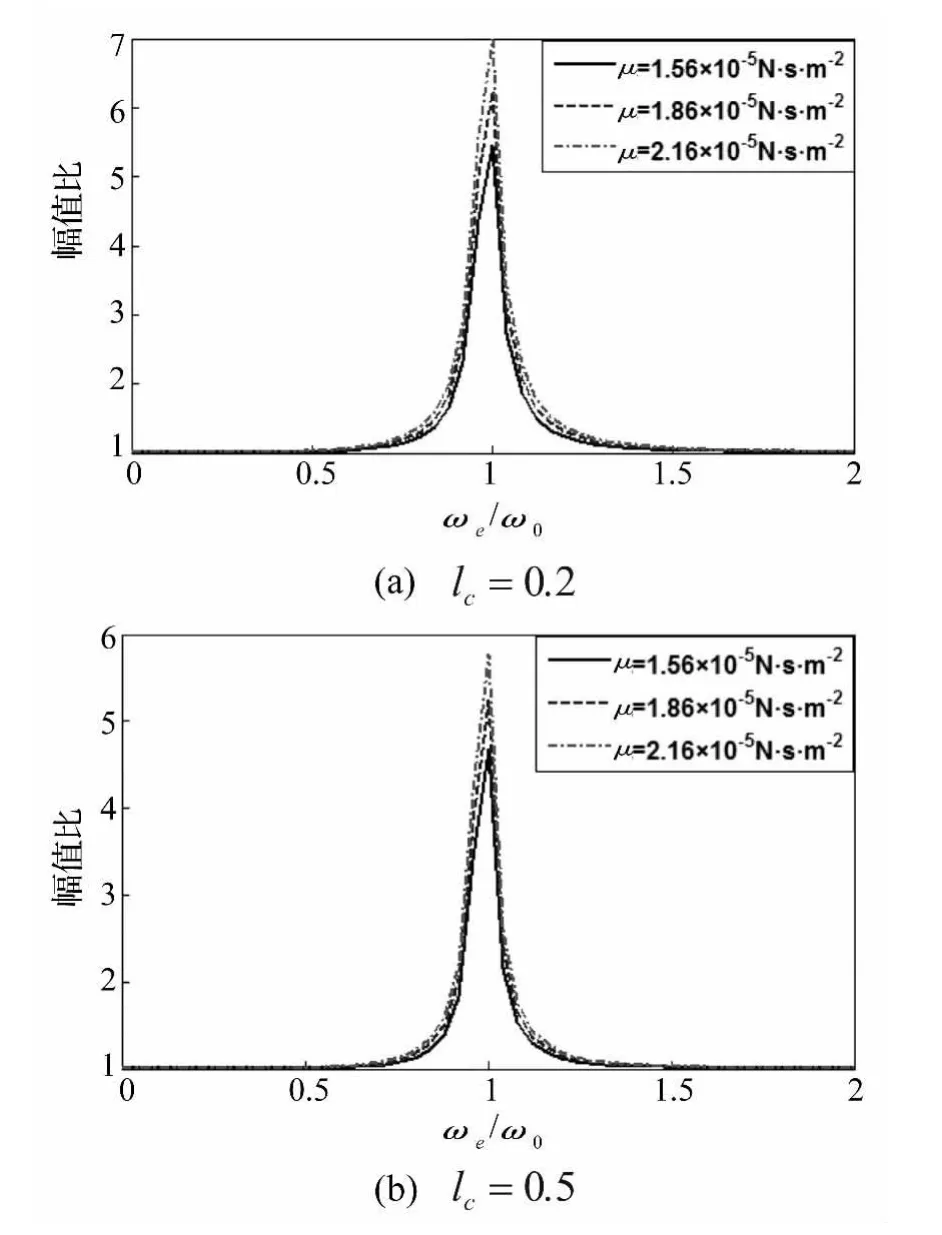
圖6 壓膜阻尼對裂紋微梁幅值的影響(K=0.5，Vp=60 V，Vt=6V)Fig.6 The effects of squeeze film damping on amplitude of cracked microbeam(K=0.5，Vp=60 V，Vt=6V)

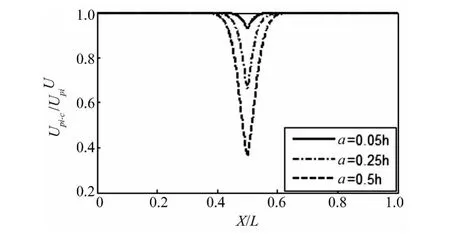
圖7 正則化裂紋梁吸合電壓的變化(裂紋位置 lc=0.5)Fig.7 Variation of normalized pull-in voltage(lc=0.5)

3 結(jié)論

以靜電驅(qū)動裂紋微懸臂梁為研究對象，采用無質(zhì)量轉(zhuǎn)動彈簧模型模擬裂紋，考慮壓膜阻尼效應(yīng)，建立了系統(tǒng)動力學(xué)模型，對系統(tǒng)的自由振動、受迫振動以及吸合電壓進行了研究。得到以下幾點結(jié)論:

(1)一階模態(tài)時，開裂程度越大，裂紋越靠近懸臂梁根部，固有頻率越小。高階模態(tài)時，開裂程度對梁固有頻率的影響與裂紋位置離相應(yīng)模態(tài)節(jié)點和反節(jié)點的遠近程度有較大的關(guān)系。特別是，當裂紋位于模態(tài)節(jié)點時，開裂程度對固有頻率沒有影響;而當裂紋位于模態(tài)反節(jié)點時，固有頻率受開裂程度的影響最大。隨加載電壓的增加以及電極間隙減小，固有頻率逐漸減小。

(2)隨著直流偏置電壓和交流電壓幅值的增大以及氣體動力粘度的減小，系統(tǒng)的振幅隨之增大。在相同情況下，裂紋越靠近懸臂梁根部，系統(tǒng)的振幅越大。

(3)對靜電驅(qū)動裂紋微懸臂梁結(jié)構(gòu)的振動特性進行分析，有助于微器件的設(shè)計、性能改進及健康檢測。

［1］Bing G，Quate C F，Gerber C.Atomic force microscope［J］.Physic Review Letter，1986，56:930 －934.

［2］AlbrechtT R， Akamine S， Carver T E， etal.Microfabrication of cantilever styli for atomic force microscope［J］.Journal of Vacuum Science and Technology，1990，8(4):3386－3389.

［3］Sayanu P，Robert P，Kris B，et al.Pull-in voltage analysis of electrostatically actuated beam structures with fixed fixed and fixed free end conditions［J］.Journal of Micromechanics and Microengineering，2002，12(4):458－464.

［4］Slava K，Ronen M.Pull-in dynamics of an elastic beam actuated by continuously distributed electrostatic force［J］.Journal of Vibration and Acoustics，2004，126:332 －342.

［5］Fadi M A，Mohammad I Y，Hassen M Q.On the nonlinear resonances and dynamic pull-in of electrostatically actuated resonators［J］. Journal of Micromechanics and Microengineering，2009，19:1－14.

［6］Zhang W H，Baskaran R，Turner K L.Effect of cubic nonlinearity on auto-parametrically amplified resonant MEMS mass sensor［J］.Sensors and Actuators A:Physical，2002，102(1－2):139－50.

［7］李 普，胡如夫，尹 垚.彈性懸臂微梁諧振系統(tǒng)擠壓模阻尼新解析模型［J］.振動與沖擊，2008，27(3):5－14.LI Pu，HU Ru-fu，YIN Yao.A new analytical model of squeeze film damping for resonance system of flexible microcantilever beam［J］.Journal of Vibration and Shock，2008，27(3):5－14.

［8］Fernandez-Saez J，Navarro C.Fundamental frequency of cracked beams in bending vibrations:an analytical approach［J］.Journal of Sound and Vibration，2002，256(1):17－31.

［9］Zhong S C，Oyadiji S O.Analytical predictions of natural frequencies ofcracked simplysupported beamswith a stationary roving mass［J］.Journal of Sound and Vibration，2008，311:328－352.

［10］Andreaus U，Casini P，Vestroni F.Non-linear dynamics of a cracked cantilever beam under harmonic excitation［J］.International Journal of Non-Linear Mechanics，2007，42(3):566－575.

［11］劉文光，陳國平.含裂紋懸臂梁的振動與疲勞耦合分析［J］.振動與沖擊，2011，30(5):140－144.LIU Wen-guang，CHEN Guo-ping. Coupling analysis for vibration and fatigue of a cracked cantilever beam［J］.Journal of Vibration and Shock，2011，30(5):140－144.

［12］Loutridis S，Douka E，Hadjileontiadis L J.Forced vibration behaviour and crack detection ofcracked beamsusing instantaneous frequency［J］.NDT＆E International，2005，38(5):411－419.

［13］Loya J，Lopez-Puente J，Zaera R，et al.Free transverse vibrations of cracked nanobeams using a nonlocal elasticity mode［J］.Journal of Applied Physics，2009，105:044309 －1－044309－9.

［14］Ke L L，Yang J，Kitipornchai S，et al.Flexural vibration and elastic buckling of a cracked timoshenko beam made of functionally graded materials［J］.Mechanics of Advanced Materials and Structures，2009，16(6):488－502.

［15］Hasheminejad S M，Gheshlaghi B，Mirzaei Y，et al.Free transverse vibrations of cracked nanobeams with surface effects［J］.Thin Solid Films，2011，519:2477 －2482.

［16］Armstrong D E J，Haseeb A S M A，Roberts S G，et al.Nanoindentation and micro-mechanical fracture toughness of electrodeposited nanocrystalline Ni W alloy films［J］.Thin Solid Films，2012，520:4369 －4372.

［17］Osterberg P M， Gupta R K， Gilbert J R， et al. A quantitative model for the measurement of residual stress using electrostatic pull-in of beams Proc［R］.Solid-State Sensor and Actuator Workshop，1994:184－188.

［18］Christides S，Barr A D S.One-dimensional theory of cracked Bernoulli-Euler beams［J］.Journal of Mechanical Sciences，1984，26(11－12):639－648.

［19］孟 光，張文明.微機電系統(tǒng)動力學(xué)［M］.北京:科學(xué)出版社，2008.