慣性導航平臺角振動抑制技術

周亞東 董萼良 吳邵慶 韓曉林 張 鵬 費慶國

(東南大學土木工程學院，南京 210096)

(東南大學江蘇省工程力學分析重點實驗室，南京 210096)

慣性導航平臺角振動抑制技術

周亞東 董萼良 吳邵慶 韓曉林 張 鵬 費慶國

(東南大學土木工程學院，南京 210096)

(東南大學江蘇省工程力學分析重點實驗室，南京 210096)

為了抑制慣性導航平臺的角振動，基于隔振理論，建立了具有彈性支承的六自由度剛體在基座位移激勵下的振動微分方程.分析了振動方程解耦的參數條件;依據慣導平臺減振系統線振動固有頻率盡可能低、角振動固有頻率盡可能高的設計原則，利用抗扭軟軸來增加系統的角剛度，并采用有限元模型進行了數值仿真.模態分析結果表明，設置抗扭軟軸后，角振動模態頻率提高至無抗扭軟軸時的2.3倍左右，且對線振動模態頻率不產生影響.頻率響應分析結果表明，抗扭軟軸能夠提高平臺角振動固有頻率，表征角振動的位移頻率響應共振頻率由27 Hz提升至64 Hz左右，并且角剛度的增大使角偏移降低了一個數量級.由此表明，采用抗扭軟軸來增大慣導平臺減振系統角剛度、抑制角振動是有效可行的.

慣性導航平臺;角振動;減振;抗扭軟軸;角剛度

慣性導航系統是利用加速度計和陀螺等慣性元件來測量載體相對于慣性空間的線運動和角運動參數，并經計算后實施導航任務的裝置，具有導航精度高、自主性強、提供導航參數多等優點，是保證飛行安全、提高飛行器導航能力的重要設備［1］.慣性平臺組件作為一種慣性坐標基準與慣性測量裝置，其靜動態力學性能直接影響著慣性儀表的工作精度，進而影響飛行器的飛行精度［2］.對于平臺系統而言，載機的振動激勵影響其導航精度，是主要的不利因素之一.因此，研究慣性導航組件的減振技術，針對其特點設計出滿足動力學指標的高性能減振系統，對于增強慣性平臺的抗振動和抗過載能力、提高其導航精度與穩定性具有重要意義.

平臺減振設計主要從以下3個方面考慮［3］:①在載機激勵下，慣性平臺的角振動與線振動產生耦合，導致測量系統中引入偽運動信號，影響慣導系統的測量精度，因此避免或盡量減小振動耦合是慣導系統減振設計的首要目標;②為了減小減振器對系統角運動測量的干擾，要求減振系統的角振動固有頻率盡可能遠離慣導系統的測量帶寬，即要求減振系統的角振動固有頻率盡可能高;③ 在寬頻隨機激勵下，減振系統固有頻率越低，減振效率越高，因此要求減振系統的線振動固有頻率盡可能低.目前，國內外廣泛采用的三向等剛度減振器代表著這一領域的先進水平［4］.但三向等剛度減振器在抑制角振動方面仍存在較大的提升空間.

本文從研究六自由度角、線振動解耦著手，重點探討了在不改變平臺系統線振動固有頻率的情況下抑制角位移的減振方法.

1 六自由度振動解耦分析

慣導平臺的剛度遠大于隔振橡膠，故在建立動力學模型時，將其視為六自由度剛體，其振動自由度包含3個方向的線振動和3個方向的角振動.在減振系統設計中，應盡可能解除平臺剛體六自由度之間的振動耦合，這樣既便于減小可能激起共振響應的頻帶寬度，又便于合理配置其固有頻率，使共振頻率遠離激勵頻率，以獲得良好的整體隔振效果［5］.

1.1 振動微分方程

為了描述剛體的振動，需要定義以下3個坐標系:①定坐標系ˉO-ˉxˉyˉz，即運動的慣性參考系;②動坐標系O-xyz，固結于振動剛體;③ 動坐標系O1-x1y1z1，固結于基座.六自由度剛體振動系統如圖1所示.

假設在沒有發生振動時3個坐標系重合，且原點均位于剛體質心.假設剛體相對于定坐標系的振動位移向量 X={x，y，z，θx，θy，θz}T，基座相對于定坐標系的激勵位移向量 U={ux，uy，uz，φx，φy，φz}T，則在基座位移激勵下，剛體的振動微分方程為

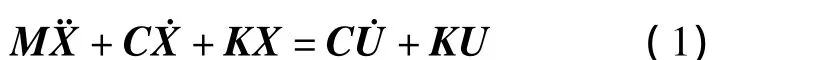
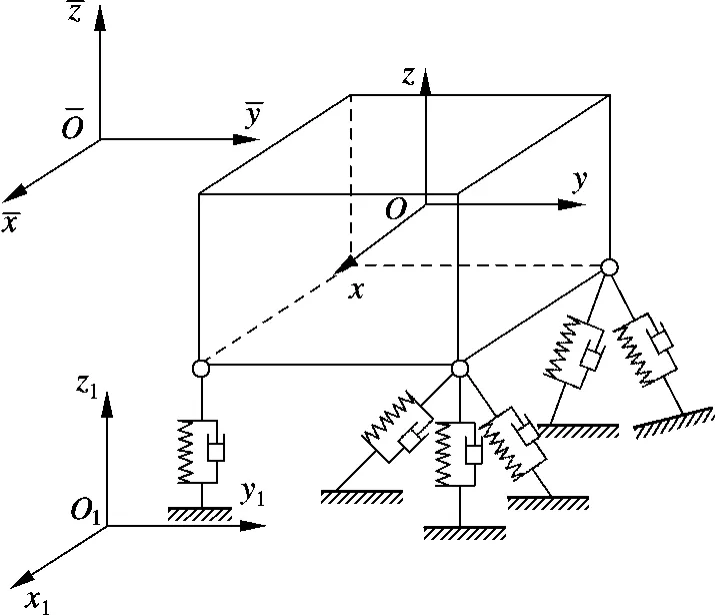
圖1 六自由度剛體振動系統

式中，M為慣性矩陣，且

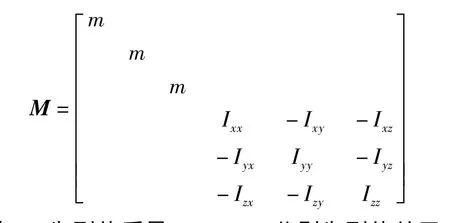
其中，m為剛體質量;Ixx，Iyy，Izz分別為剛體關于x，y，z軸的慣性矩;Ixy為剛體關于x，y軸的慣性積;Iyx，Iyz，Izy，Ixz，Izx的物理含義以此類推.K 為剛度矩陣，且

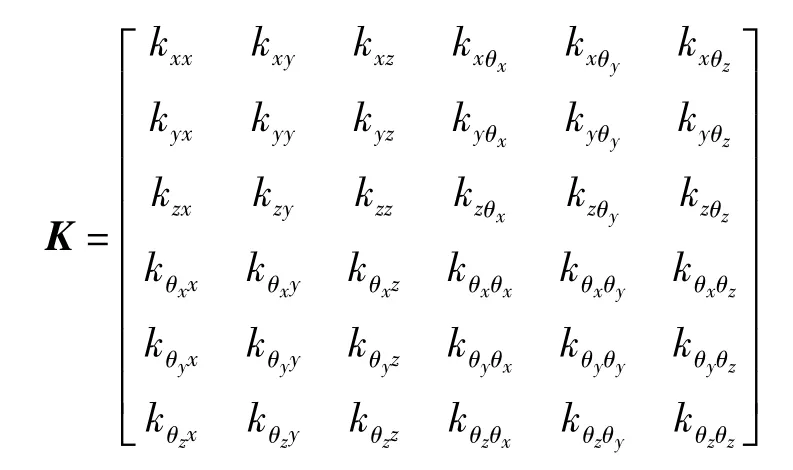
其中，各元素為剛度系數，元素kxy表示僅使y自由度發生單位位移時x自由度所需的廣義力，其余元素的物理含義以此類推.C為阻尼矩陣，其中各元素為黏性阻尼系數，與剛度系數形式類似，即

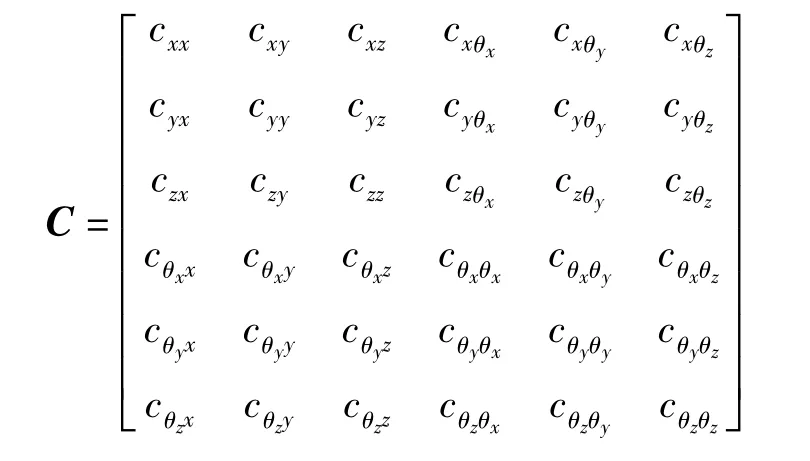
其中，cxy表示僅使y自由度獲得單位速度時x自由度所需的廣義力，其余元素的物理含義以此類推.

1.2 方程解耦的條件

若矩陣M，K，C為對角陣，則六自由度剛體可實現振動解耦.解耦的條件如下:

1)若動坐標系O-xyz的坐標軸與剛體的慣性主軸重合，則慣性矩陣中非對角元素Ixy=Iyx=Iyz=Izy=Ixz=Izx=0.

2)若彈性隔振元件的3個彈性主軸分別與坐標系O-xyz的坐標軸方向一致，則kxy=kyx=kyz=kzy=kxz=kzx=0.

3)若隔振系統存在1個或多個對稱面，則可使各系數矩陣非對角元部分甚至全部置零.例如，若隔振系統關于O-xy面對稱，則剛體在O-xy面的平動與z向的平動以及繞z軸的轉動不耦合，即kxz=kzx=kyz=kzy=kxθz=kθzx=kyθz=kθzy=0.

阻尼耦合與剛度耦合相似，但由于阻尼機理復雜，難以給出準確的數學表達，且其對系統共振頻率影響較小.因此，在分析系統角振動與線振動固有頻率時可忽略阻尼耦合.

綜上所述，可得如下的一般性結論:若彈性隔振元件的彈性中心與剛體質心重合、彈性主軸與慣性主軸重合，則各系數矩陣為對角陣［6］.在實際應用中，若使隔振器和被隔振對象安裝后具有3個對稱面，則滿足結論要求，六自由度方程解耦［7］.通常，慣性導航組件橡膠隔振系統安裝有8個上下對稱布置的隔振器［8］，因此理論上滿足振動方程解耦的條件.

1.3 參數解耦計算

方程解耦后，轉化為6個單自由度系統的振動方程，即

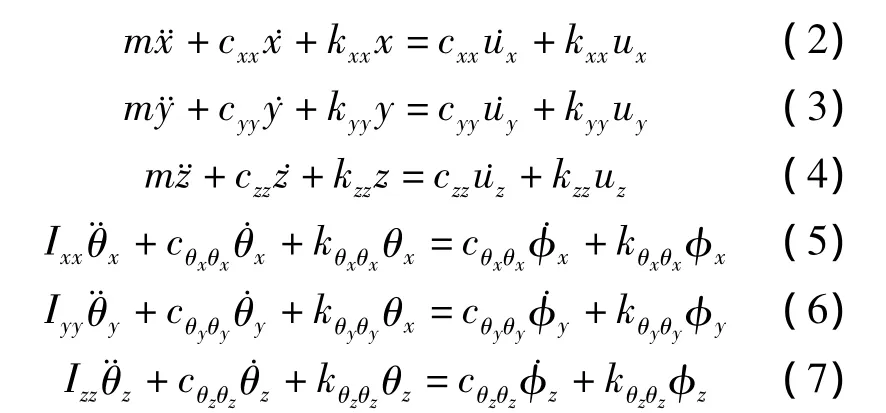
系統中6個無阻尼固有頻率分別為

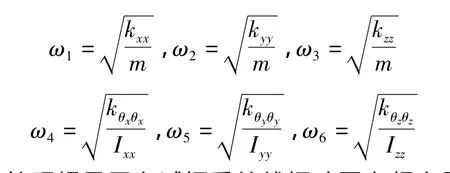
按照慣導平臺減振系統線振動固有頻率盡可能低、角振動固有頻率盡可能高的設計思想，在慣導平臺質量既定的情況下，要降低線振動固有頻率必須降低線剛度，同時還需滿足靜態支承條件.角振動固有頻率的增加，可以通過提高扭轉剛度和降低主轉動慣量來實現;目前，則主要通過改變減振器的布置方式，使平臺質量分布盡量集中于中心來實現.在實際安裝時，應盡量保證對稱性以使振動去耦.

2 抗扭軟軸

抗扭軟軸通常由若干層鋼絲在芯棒表面交替繞制而成.每層布設4～12根高強度鋼絲，相鄰層之間鋼絲繞制方向相反［9］.其內部結構如圖2所示.

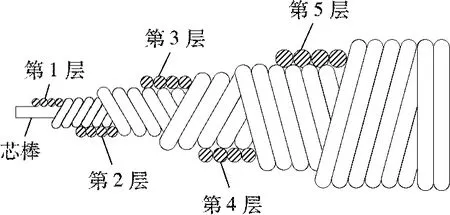
圖2 抗扭軟軸內部構造

軟軸具有優良的空間性能，可以將扭矩或旋轉運動靈活地傳遞到所需的位置.按照用途不同，軟軸可分為功率型和控制型，其中控制型軟軸鋼絲層數及每層鋼絲根數較多，抗扭剛度大［10］.由軟軸傳遞扭矩時，相鄰2層鋼絲中一層趨于繞緊，另一層趨于旋松，從而使各層鋼絲間趨于壓緊.軟軸接頭用于連接軟軸與傳動部件(或被傳動部件).連接的方式有固定式和滑動式，其中滑動式連接允許軟軸在軟管內有較大的竄動.

相對于剛性軸而言，抗扭軟軸在傳動或制動時具有可以彎曲的特點，即在保證扭轉剛度的前提下，軟軸的橫向剛度非常低.這一優良的機械性使之適用于要求高角剛度、低線剛度的場合.因此，在慣導平臺組件與載機之間，沿3個正交方向合理布置3根軟軸，能夠限制慣性平臺的角振動.在平臺組件與載機的連接處，可以使用滑動式連接，使之不影響線剛度.

3 數值仿真

下面通過建立一有限元模型，來檢驗抗扭軟軸對改善系統角振動狀況的有效性.對慣導平臺和橡膠減振器進行簡化，采用鋁質實體單元來模擬平臺臺體，外框為鋼板，使用殼單元.臺體與外框架之間為減振橡膠，使用尺寸較小的實體單元建模.模型單元總數為12 148，節點總數為12 745，并將其記為模型A.為了分析增加角剛度的效果，在模型A的基礎上，于平臺臺體與外框架之間沿X軸方向設置具有扭轉剛度的連接單元，以模擬抗扭軟軸，并將其記為模型B.根據機械設計手冊［10］，精密控制軸的扭轉角可限制在0.25(°)/m以內;在額定轉速1 150 r/min下，直徑19 mm的軟軸可承受的最大扭矩為2 kN·cm;模型中平臺左側與框架左側的X軸方向距離為100 mm.據此設置連接單元的X向扭轉剛度為5 kN·m/rad，其他2個方向扭轉剛度及3個線剛度均為零.模型A，B的邊界條件均為在框架4個拐角處固支，所用材料的物理參數見表1.圖3為有限元模型B.

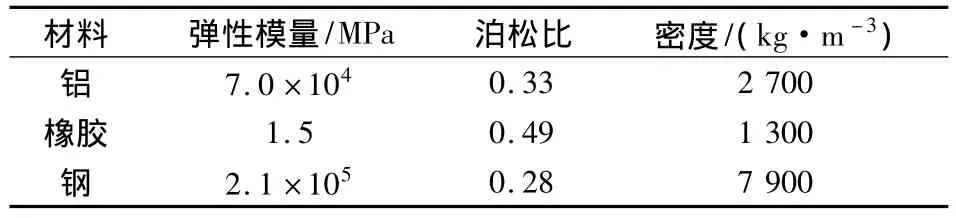
表1 模型材料物理參數

圖3 有限元模型B

3.1 正則模態分析

對模型A，B分別進行正則模態分析，計算出模型的固有頻率和模態振型.系統前6階模態為平臺的3個平動模態和3個轉動模態，6階以上模態為彈性模態.

下面分析平臺繞X軸的轉動模態(對應于系統的第6階模態).表2列出了模型A，B的前6階固有頻率.由表可知，在設置X方向扭轉剛度后，系統的第6階角振動固有頻率提高至原先的2.3倍左右，其他階模態頻率則幾乎不變.

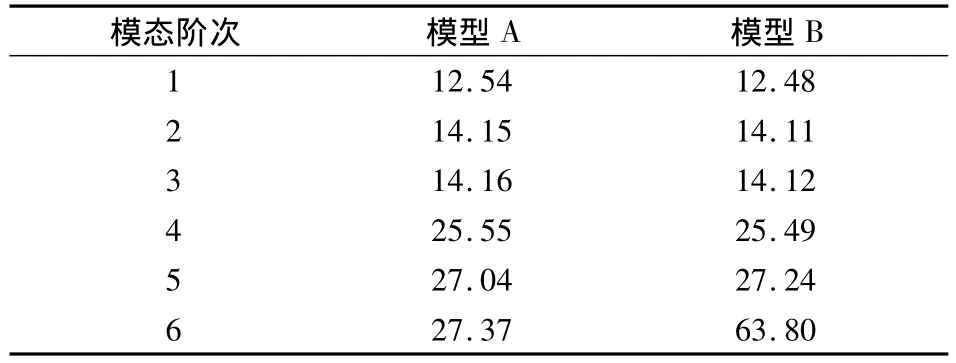
表2 模型A，B的固有頻率 Hz

3.2 頻率響應分析

為了研究非對稱激勵下平臺的動響應，在平臺一角點處沿Y方向施加100 N的正弦激勵力.平臺的前6階模態頻率在100 Hz以內，故設置頻率響應分析的頻率范圍為0～100 Hz.此處不詳細探討減振橡膠的阻尼效應，僅設置結構的全局結構阻尼系數為 0.05.

將激勵點相鄰節點的平臺模型頂點作為響應點，其Y向位移對應于平臺的線振動，Z向位移對應于平臺的角振動.提取該點的計算結果，2個模型的Y向、Z向位移頻率響應曲線分別見圖4和圖5.

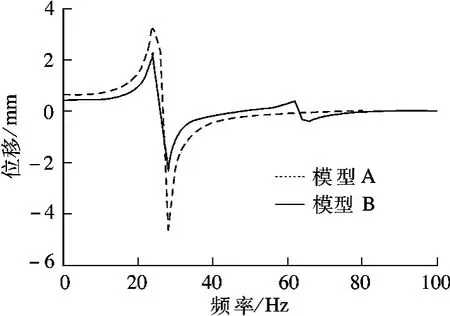
圖4 Y向頻率響應

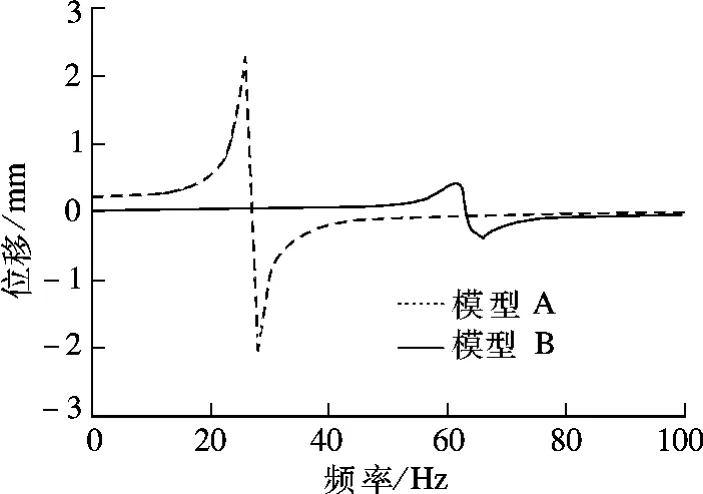
圖5 Z向頻率響應

對比圖4與圖5可知，增加抗扭剛度，響應點的Y向頻率響應曲線形狀基本不變，共振幅值略有降低，僅在約64 Hz處有輕微擾動.抗扭軟軸對響應點Z向位移響應共振頻率的移頻效果明顯，模型A，B的共振峰值分別出現在27，64 Hz左右，這與表2中的第6階固有頻率基本一致，說明抗扭軟軸有助于將平臺角振動固有頻率移向高頻.此外，角剛度增大后，Z向頻響曲線峰值降低了一個數量級.對于模型的Y面和Z面，同樣可以設置一定剛度的抗扭軟軸.鑒于軟軸良好的可彎曲性能，在實際操作中可以選擇鋼板的合適位置進行連接.

4 結語

慣性導航平臺橡膠隔振系統在保證沿3個面對稱布置時滿足振動解耦的條件，角振動與線振動不耦合，故在實際安裝時應盡可能保證系統質量分布和彈性支承的對稱性.

合理安裝抗扭軟軸，符合高角剛度、低線剛度的要求，故可應用到慣導平臺減振中以抑制角偏移.數值仿真結果表明，抗扭軟軸有助于將系統角振動固有頻率移向高頻，且角剛度的增大在一定程度上導致振動幅值減小.

［1］蘇廣中，葉樺.慣性導航系統訓練模擬器的研制［J］.東南大學學報:自然科學版，2004，34(S1):92－95.

Su Guangzhong，Ye Hua.Development of inertial navigation training simulator［J］.Journal of Southeast University:Natural Science Edition，2004，34(S1):92－ 95.(in Chinese)

［2］楊朋軍，靳長權，王佳民.慣性平臺臺體組件動態特性分析［J］.機械設計，2004，21(10):54－56.

Yang Pengjun，Jin Changquan，Wang Jiamin.Dynamic characteristic analysis for platform body component of inertial platform［J］.Journal of Machine Design，2004，21(10):54－56.(in Chinese)

［3］張志鑫，張大偉.捷聯慣組減振系統角振動、線振動共振頻率理論分析［J］.中國慣性技術學報，2009，17(6):654－657.

Zhang Zhixin，Zhang Dawei.Theory analysis on resonance frequencies of linear vibration and torsional vibration of strapdown IMU damping system［J］.Journal ofChinese Inertial Technology，2009，17(6):654－ 657.(in Chinese)

［4］葛祖德，姚起杭.航空用新型減振器［J］.應用力學學報，2001，18(S1):110－113.

Ge Zude，Yao Qihang.The vibration isolator with high damping used in aircraft［J］.Chinese Journal of Applied Mechanics，2001，18(S1):110－113.(in Chinese)

［5］呂振華，范讓林.動力總成－懸置系統振動解耦設計方法［J］.機械工程學報，2005，41(4):49－54.

Lü Zhenhua，Fan Ranglin.Design method for vibration uncoupling of powerplant-mounting system［J］.Chinese Journal of Mechanical Engineering，2005，41(4):49－54.(in Chinese)

［6］Cyril M Harris，Allan G Piersol.Shock and vibration handbook［M］.5th ed.New York:McGraw-Hill，2002.

［7］丁文鏡.減振理論［M］.北京:清華大學出版社，1988:15－18.

［8］Tuo Zhouhui，Hu Dewen，Li Ruhua，et al.Damping design of strapdown inertial navigation system［J］.Journal of Chinese Inertial Technology，2009，17(6):648－650.

［9］丁言勇.軟軸在飛行器上的應用［J］.航空制造技術，2010(19):102－103.Ding Yanyong.Application of soft shaft in aircraft［J］.Aeronautical Manufacturing Technology，2010(19):102－103.(in Chinese)

［10］機械設計手冊編委會.機械設計手冊:第19篇［M］.3版.北京:機械工業出版社，2009:3－42.

Restricting method for angular vibration of inertial navigation platform

Zhou Yadong Dong Eliang Wu Shaoqing Han Xiaolin Zhang Peng Fei Qingguo

(School of Civil Engineering，Southeast University，Nanjing 210096，China)
(Jiangsu Key Laboratory of Engineering Mechanics，Southeast University，Nanjing 210096，China)

To reduce the angular vibration of inertial navigation platform，an oscillatory differential equation for six degrees of freedom elastically-supported rigid body with base displacement excitation was established based on the theory of vibration isolation.The condition of equation decouple was analyzed.According to the principle that the translational vibration frequency should be as low as possible and the angular vibration frequency should be as high as possible，torsion-resistant flexible shaft was adopted to improve the angular stiffness of the inertial navigation platform system.Numerical simulation was carried out by finite element model.The results of modal analysis show that the modal frequency of angular vibration with the fixed torsion-resistant flexible shaft is about 2.3 times that of the state without torsion-resistant flexible shaft.And the torsion-resistant flexible shaft has no effect on the modes of translational vibration.The frequency response analysis results show that the torsion-resistant flexible shaft can improve the angular resonant frequency.The resonant frequency of displacement frequency response which can mirror the angular vibration is improved from about 27 to 64 Hz.And the angular deviation is reduced by an order of magnitude with the increase of the angular stiffness.This indicates that torsion-resistant flexible shaft is effective in augmenting angular stiffness and restricting angular vibration.

inertial navigation platform;angular vibration;vibration reduction;torsion-resistant flexible shaft;angular stiffness

O328;V249.322

A

1001－0505(2013)01-0060-05

10.3969/j.issn.1001－0505.2013.01.012

2012-06-08.

周亞東(1987—)，男，博士生;費慶國(聯系人)，男，博士，副教授，博士生導師，qgfei@seu.edu.cn.

國家自然科學基金資助項目(10902024)、教育部新世紀優秀人才支持計劃資助項目(NCET-11-0086)、江蘇省自然科學基金資助項目(BK2010397)、航空科學基金資助項目(20090869009).

周亞東，董萼良，吳邵慶，等.慣性導航平臺角振動抑制技術［J］.東南大學學報:自然科學版，2013，43(1):60－64.［doi:10.3969/j.issn.1001－0505.2013.01.012］