基于粒子群優化算法的室內定位方法
王小斌 關維國 程 猛 慕文靜
(遼寧工業大學電子信息工程學院 遼寧 121001)
0 引言
定位技術是無線傳感器網絡的主要支撐技術之一。獲取傳感器節點的位置信息是傳感器網絡應用的一種重要組成部分,在室內進行無線傳感器節點位置定位成為研究熱點。
為了提高節點的定位精度,將粒子群優化算法引入到無線傳感器網絡定位中,通過迭代算法尋求最優解。
文獻[1]將粒子群優化算法與質心定位算法相結合,定位效果好,但是過程比較復雜,定位精度沒有明顯的提高。
文獻[2]把混沌尋優思想引入到粒子群優化算法中,在參數合理設置的前提下,算法性能穩定,并且具有較快的定位速度和較高的定位精度。
1 粒子群優化算法描述
1.1 粒子群優化算法的數學描述[3]
假設在一個 D維的空間中,有 N個代表存在問題解的粒子組成一個初始群體,其中,每一個粒子都可以表示為一個D維的向量:第 i個粒子在D維空間中的位置是 Xi,粒子更新速度令 Pi為第i個粒子目前為止搜索到的個體最優位置解所對應的位置坐標,令 Pg為粒子群目前為止搜索到的全局最優位置解所對應的位置坐標每次迭代中粒子按照式(1)、(2)更新速度與位置:
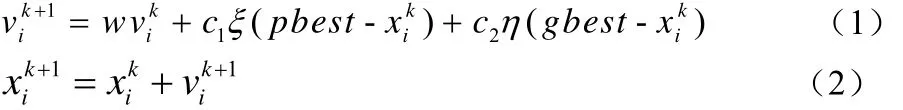
式中i= 1,2,3...,N ; k為迭代次數;w為慣性權重; c1,c2為學習因子;ξ,η是隨機數。pbest為個體最優值;gbest為全局最優值。粒子通過不斷的自身總結和學習更新,最后找的 Pg就是全局最優解。
1.2 粒子群優化算法參數[4][5]
參數一為常用的固定參數: w = 0 .6, c1 = c 2 = 1 .7。
參數二引入壓縮因子的粒子群優化算法, w = 0 .6,c1 = c 2 = 1 .494。
1.3 適應度函數
適應度函數用來評價粒子群優化算法中各個粒子在種群中接近于最優解的優劣程度,從中選取每個粒子的個體最優解和種群的全局最優解。
適應度函數一:設為求未知節點估計位置到各個信標節點距離與測量距離差的方差最小值問題。

此函數值越小,得到的位置解越優。
適應度函數二:基于測距的定位算法中n個信標節點可得n個距離公式,進而可以線性化為 n -1維的矩陣方程Ax=B,由于實際中誤差存在,設xAx+ N = B,N為 n -1維的誤差向量,借用最小二乘法的原理, 的值應該是誤差向量N = B - A x達到最小值的取值,即用最小化Q(x) = N2= B- A x2求x的估計,同時引用加權最小二乘法,引入N的協方差矩陣 cov(N),令適應度函數為(4)式:

2 仿真結果及分析
設節點的通信范圍是在 20m×20m 的平面室內區域內,信標節點坐標分別為A(0,0),B(0,20),C(20,0),D(20,20)。未知節點坐標為E(13,9)。
粒子群的種群大小 40N= ,將總的迭代次數 100T= ,經MATLAB7.1進行仿真實驗,為便于觀察,適應度函數里距離id取值為未知節點E到信標節點真實距離,得圖1為三種參數(2.2中)的適應度函數值收斂曲線對比圖。
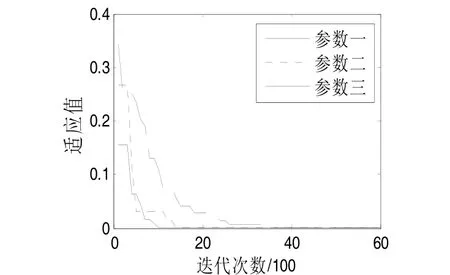
圖1 收斂曲線對比圖
由圖1可知,選擇參數一的情況下大約迭代50次逐漸趨于平穩;選擇參數二的情況大約迭代30次;選擇參數三大約迭代20次。
以下是適應度函數一與適應度函數二定位誤差的比較,為盡量減少迭代次數,使用參數三,仿真結果如圖2所示。
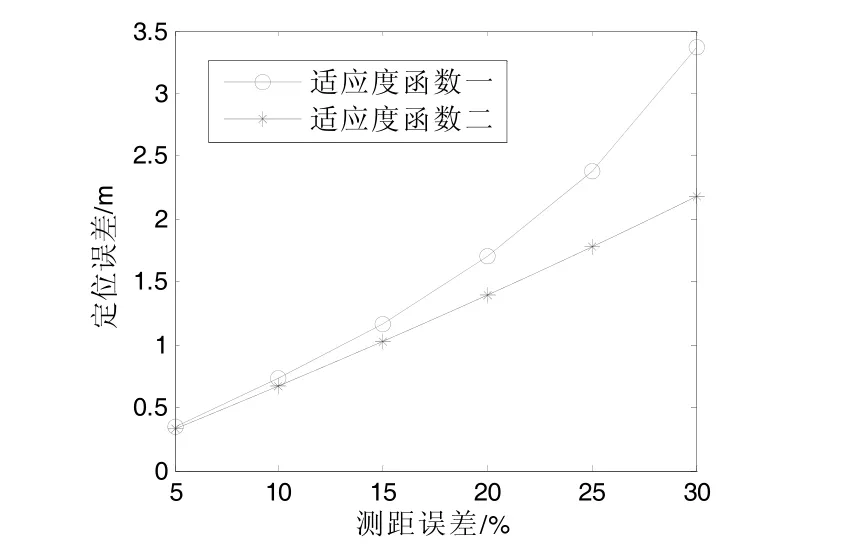
圖2 定位誤差圖
適應度函數二比適應度函數一有更好的定位效果,這是因為應用粒子群優化算法,無論在測距誤差較小還是較大情況下,都能通過多次迭代尋找最優解,從而減弱了測距誤差引入的噪聲影響。
3 結 論
與經典的粒子群濾波算法相比,本文通過修改參數,減少了迭代次數,降低了算法復雜度,應用新的適應度函數,與傳統的適應度函數相比,新的適應度函數因為取誤差公式的最小化估計,比單純的優化誤差的最小值更能得到精確的位置坐標,定位精度有明顯提高。
[1]王新芳,張冰,馮友兵.基于粒子群優化的改進加權質心定位算法[J].網絡與通信,2012,38(01):90-95.
[2]史洪宇,燕莎,曹建忠.無線傳感器網絡節點定位的混沌粒子群優化算法[J].探測與控制學報,2010,32(5):46-49.
[3]雷秀娟,史忠科.粒子群優化算法在函數優化中的應用及參數分析[J].計算機工程與應用.2008,44(28):53-55.
[4]王俊偉,汪定偉.粒子群算法中慣性權重的實驗與分析[J].系統工程學報,2005,20(2):194-198.
[5]魯雅靜.基于粒子群優化算法的無線傳感器網絡節點定位技術研究[D].合肥:合肥工業大學,2012.
[6]王曉樂,徐家品.基于粒子群優化算法的WSN節點定位研究[J].計算機應用,2009,29(02):494-499.
[7]陳志奎,司威,傳感器網絡的粒子群優化定位算法[J].通信技術,2011,44(01):102-108.

