線性規(guī)劃靈敏度分析的一個應(yīng)用

楊大勇

（隴東學院 數(shù)學與統(tǒng)計學院，甘肅 慶陽 745000）

線性規(guī)劃模型如下

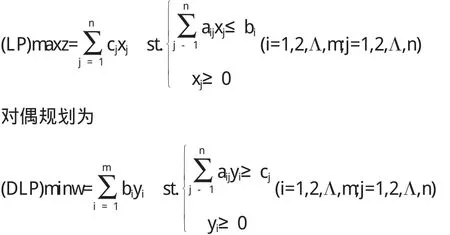
現(xiàn)在對線性規(guī)劃問題(LP)化成標準型(LP')可運用單純形法得到最優(yōu)表,設(shè)T(B)為對應(yīng)的最終單純形表,簡記為：

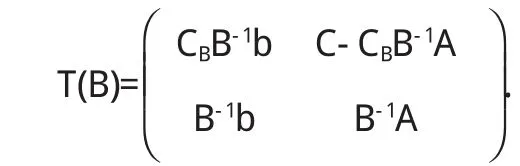
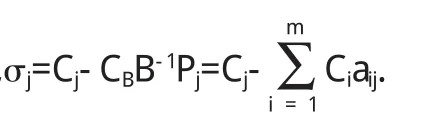
對線性規(guī)劃模型(LP)在增加約束條件的情況[1]中做了詳細的說明.而對線性規(guī)劃模型(LP)在減少約束條件時進行靈敏度分析,教材中提的較少.因為迭代過程已將要去掉的約束條件經(jīng)過行初等變換作用于其它約束條件以及目標函數(shù)中,對整個迭代過程都產(chǎn)生了影響.

在前面的最終表T(B)中,最優(yōu)基B的逆矩陣為B-1,線性規(guī)劃模型(LP)的原m×n階系數(shù)矩陣為A,在最終表T(B)中為即.要將第i個方程去掉,就須使第i個約束條件失靈.處理方法可在第i個約束條件左邊添加兩個非負虛擬變量的差xn+m+1-xn+m+2.[4]

因此,現(xiàn)將去掉第i個約束條件的靈敏度分析的基本思路及步驟歸納如下：

1）確定B-1的第i列向量B-1Pi;

2）在最優(yōu)表中系數(shù)矩陣的最后添加B-1Pi和-B-1Pi;

3）計算相應(yīng)的檢驗數(shù)-CBB-1Pi和CBB-1Pi,并添加到T(B)相應(yīng)檢驗數(shù)行中;

4）判斷最優(yōu)性：若CBB-1Pi=0,刪掉xn+m+1或xn+m+2對應(yīng)的系數(shù)行（第i行）得到所求最優(yōu)解;若CBB-1Pi≠0,則轉(zhuǎn)入第5步;

5）刪掉xn+m+1和xn+m+2對應(yīng)的系數(shù)列,則得到新的單純形表，采用單純形法繼續(xù)迭代.

例1 如下線性規(guī)劃模型：maxz=-5x1+5x2+13x3

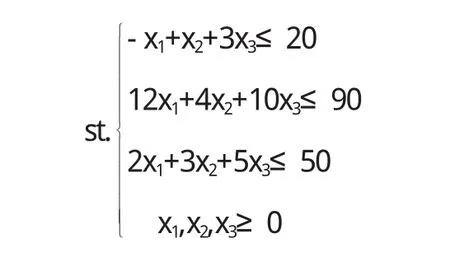
用單純形法求解并回答：若在原問題中減少第三個約束條件,這對于最優(yōu)解有何影響？

解 先將原問題化為標準型，則可列出初始單純形表,運用單純形法進行迭代求解,可得最終單純形表.于是知道原問題的最優(yōu)解為.現(xiàn)在要將第三個設(shè)備約束條件去掉,需要經(jīng)過以下步驟來實現(xiàn)：

由于要將第三個設(shè)備約束條件去掉,從最終單純形表中可以得出,從而有.則修改原問題的最終單純形表,得表

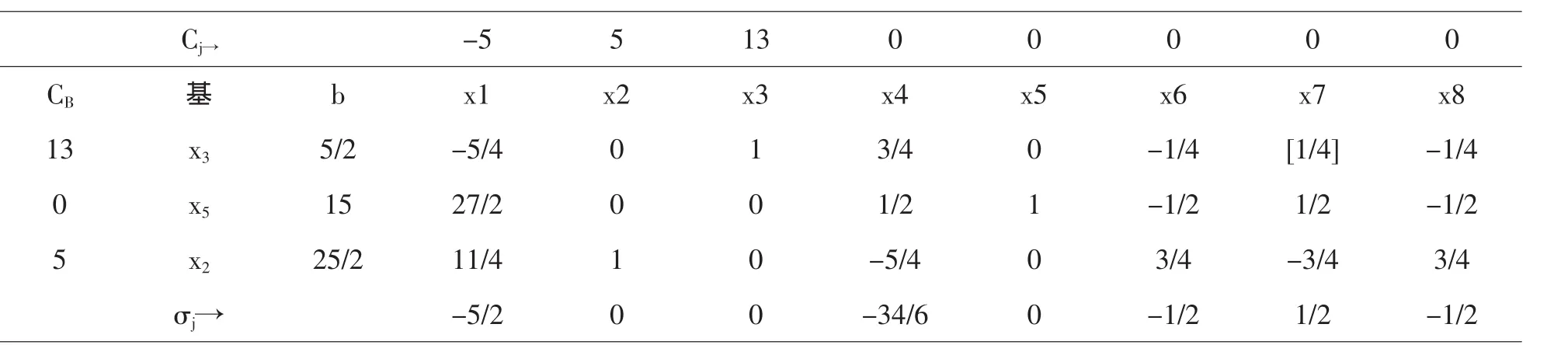
Cj→-5 5 13 0 0 0 0 0 CB基b x1 x2 x3 x4 x5 x6 x7 x813 x3 5/2-5/4 0 1 3/4 0-1/4 [1/4]-1/40 x5 15 27/2 0 0 1/2 1-1/2 1/2-1/25 x2 25/2 11/4 1 0-5/4 0 3/4-3/4 3/4 σj→-5/2 0 0-34/6 0-1/2 1/2-1/2

判別最優(yōu)性,不符合條件,則x7進基,x3出基,主元素為，采用單純形法繼續(xù)迭代,得

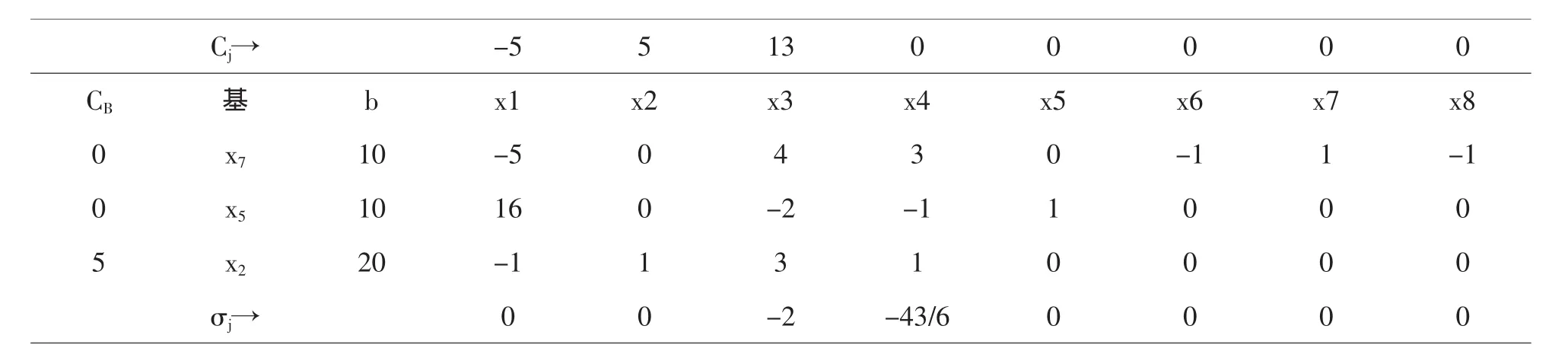
Cj→-5 5 13 0 0 0 0 0 CB基b x1 x2 x3 x4 x5 x6 x7 x80 x7 10-5 0 4 3 0-1 1-10 x5 10 16 0-2-1 1 0 0 05 x2 20-1 1 3 1 0 0 0 0 σj→ 0 0-2-43/6 0 0 0 0

刪去表中基變量x7對應(yīng)的系數(shù)行及x7和x8對應(yīng)的系數(shù)列,顯然,松弛變量x6對應(yīng)的系數(shù)列也可被同時刪去了,再判別最優(yōu)性,已經(jīng)符合條件,迭代停止.最優(yōu)解為:X*=(0,20,0,0,10)T,z*=100.

本文主要針對減少約束條件的情形來對如何求最優(yōu)解進行了討論,最后給出了實例,將方法討論中的理論付諸于實踐,更有效地說明了理論的可行性和實用性.

〔1〕胡運權(quán).運籌學[M].北京：清華大學出版社,2003.5.

〔2〕楊桂元.影子價格及其靈敏度分析[J].運籌與管理,2002,11（6）:12-13.

〔3〕李蘇北.運籌學基礎(chǔ)[M].成都：四川大學出版社,2003.1.

〔4〕解心江.線性規(guī)劃模型減少約束時的靈敏度分析[J].農(nóng)業(yè)系統(tǒng)科學與綜合研究.2002,18（3）：178-179.

〔5〕徐渝,賈濤.運籌學（上冊）[M].北京：清華大學出版社,2005.2.

〔6〕劉滿鳳,傅波,聶高輝.運籌學模型與方法教程例題分析與題解[M].北京：清華大學出版社,2001.2.

〔7〕傅家良.運籌學方法與模型[M].上海：復旦大學出版社,2006.1.