Excel中規劃求解在集裝箱班輪航線系統配船中的應用

文/郭海濤 施洪健

航線配船與船隊規劃是合理配置航運企業有限資源的重大決策，它關系到企業的經濟效益，影響到企業的競爭力和發展。因此，國內外許多學者對此做了大量研究。例如，文獻[1]研究了新組建船隊的規劃問題，文獻[2]建立了基于不確定性的動態船隊規劃模型，文獻[3]采用粒子群優化算法建立了不確定性的航線配船模型。這些研究在理論上都是成功的，但模型都十分復雜且解法繁瑣， 非專業人員很難掌握，無法應用于企業實踐。文獻[4]提出了船隊規劃的線性規劃、非線性和動態規劃模型，利用線性規劃與動態規劃相結合的算法，開發了計算機軟件包進行求解，將研究向實用化推進了一步。但是受船公司管理人員專業知識所限，對于軟件包解題規模和使用范圍認識有限，無法準確理解計算機語言，難以應用于航運企業的系統配船。因此，本文針對傳統航線配船和船隊規劃方法難以應用于實踐中的問題，建立了航線配船與船隊規劃數學模型，并采用線性規劃中的整數規劃的方法開發了航線配船與船隊規劃決策系統，旨在推動excel中規劃求解在航運企業系統配船中的運用。

充分競爭的集裝箱班輪市場，外部環境若發生較大的變化，勢必影響既有航線貨運量發展。貨運量的改變，直接導致相應航線競爭日趨激烈，或在班輪公會的指導下進行運力控制。[5]作為班輪公司而言，經營多條班輪航線，分配在這些航線上的船舶類型、規模和數量各異，雖然在各航線開辟時，對航線上的配船方案都是在詳細地論證之后才確定下來的，但外部環境改變會導致原有方案不能充分達到公司的經營目的，面對市場航運公司必須盡快調整運力分配。

1.問題描述

傳統的航線配船大都采用大船配大線法則，亦即大噸位、高速船配置在航距長、裝卸效率高、貨源充足的航線上。按此法則確定的配船方案雖然在一定程度上體現了經濟上合理的原則，但不能保證其最優化。集裝箱班輪航線系統配船優化是指最合理地將班輪船隊中不同噸位（箱位）的船舶配置到公司經營的各條航線上，做到不僅要保證滿足每條航線的技術、營運方面的要求，而且能夠使船公司取得最好的經濟效益。經濟上合理則存在一個優化的問題，這是集裝箱班輪航線系統配船優化的主要研究內容。[6]

2.模型建立

集裝箱班輪公司經營發展，大多以成本最低或運量最大為目標函數，基本上都是以運力限制和貨源（運量）限制為約束條件。此模型的目標函數追求的是系統總成本的最小化，建立線性關系，形成分配問題線性規劃模型。此模型基本上反映了班輪航線的實質。

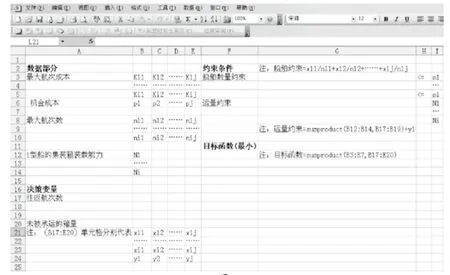
圖1

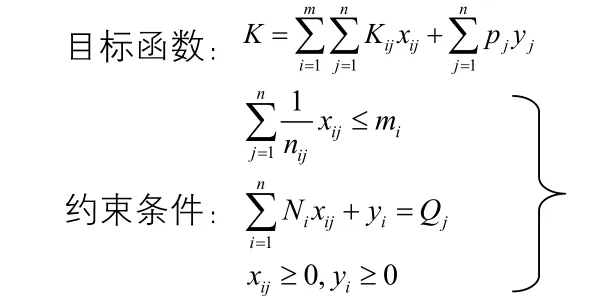
K——系統總成本

Kij——每艘i型船在j航線上完成一個往返航次所花費的成本（美元/次）

xij ——i型船在j航線上每季度完成的往返航次數，是決策變量（次/季度）

pj——j航線上1 TEU貨物的機會成本（美元/ TEU）

yj——j航線上未被船舶承運的集裝箱數量，也是決策變量（TEU）

nij——每艘i型船在j航線上每季度可以完成的最大往返航次數（次/季度）

mi——i型船的船舶數量（艘）

Ni——i型 船的集裝箱裝載能力（TEU）

Qj——j航線上得正向運量（TEU）

在此模型中，目標函數追求系統總成本最小。系統總成本包括船舶運輸成本和機會成本。約束條件中，第一個為船隊能力約束，它表示i型船分配到所有航線的船舶數量不能超過該型船的船舶總數；第二個約束條件是運輸需求約束，j航線上所有船舶完成的運輸量加上未被承運的部分正好等于該航線的運輸任務。

3.模型求解（見圖1）

步驟1 在excel表格頂部輸入數據。

步驟2 確定每個決策變量所對應的單元格的位置。

步驟3 選擇單元格輸入格式，找到目標函數的值。

步驟4 選擇一個單元格輸入公式，計算每個約束條件左邊的值。

步驟5 選擇一個單元格輸入公式，計算每個約束條件右邊的值。

4.運用舉例

現有某船公司擁有3種噸位的集裝箱船23艘，它們分別是1500 TEU集裝箱船5艘、850 TEU集裝箱船8艘、500 TEU集裝箱船10艘?，F已開辟了4條班輪航線，這些航線始發港相同，而目的港不同，分別處在不同的國家或地區。根據預測，各條航線每季度的集裝箱貨運量有6種可能的情況，具體數值列在表1中。船舶在每條航線每季度最多能完成的航次數、每艘船在各航線每往返航次的成本，以及每條航線發生的機會成本列在表2中。

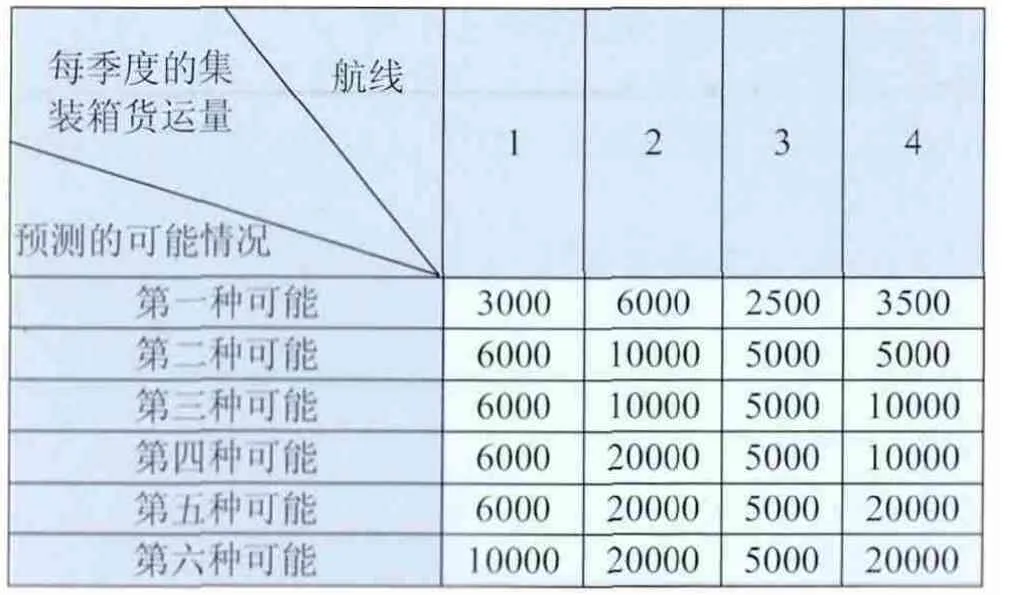
表1 各條航線每季度的集裝箱貨運量

表2 各航線的每季度最大航次數、單船單航次成本和各航線機會成本

利用excel中規劃求解，把規劃求解結果用表3列出，因可能存在的6種貨運量，所以每種情況都要通過計算機利用excel中規劃求解運算。

剩余船舶數量/艘= 型船的總數量—船舶數量約束

表3中的“---”代表數據0，意思代表航次數或未被承運的箱量。

表3 各運量方案下的航線配船結果

從表中的配船結果可以看到，在運輸任務較少時，噸位大的運輸船舶優化分配到了各條航線，而噸位較小的船舶由于單位運輸成本高而未被安排。當各條航線運量增加時，船隊中所有的船舶都被分配到相應的航線上去了，而且部分航線的一些貨載有剩余（見運量方案5、運量方案6的配船方案），這時表明船隊運力已小于運量。目標函數值，是某一運量條件下的最小運輸成本值，隨著運量的增加而增加。

5.結語

航線配船與船隊規劃問題一直是航運業關注和研究的熱點，但是實用可行的優化模型非常少。本文在追求實用性的基礎上建立了一種以船隊營運總成本最小為目標函數的優化模型。該模型根據下一季度時間內的運輸需求，預測研究這個船隊在此季度內的最優構成和船隊規劃問題。作者以excel中為規劃求解，設計開發了航線配船與船隊規劃決策系統。該系統能夠根據輸入的已知決策參數，迅速求解出相應的最優船隊調配和規劃方案，為決策者提供快速、準確的參考數據。

[1] Nicholson T A J, Pullen R D.Dynamic programming applied to ship fleet management [ J] . Operational Research Quarterly, 1971, 22( 3) : 2112220.

[2] 蘇紹娟. 不確定動態船隊規劃的數學模型研究[ J] .中國航海, 2008,31( 2)

[3] 蘇紹娟, 王麗錚, 王呈方. 不確定性航線配船數學模型建模方法[ J] . 船海工程, 2007, 36( 4) :

[4] 謝新連, 李樹范, 紀卓尚 等. 船隊規劃的線性模型研究與應用[ J] . 中國造船, 1989, ( 3) : [ 5] 趙剛. 國際航運管理(普通高等教育十五國家級規劃教材) .2006年01月