小推力轉移軌道的快速優化設計

劉柯邑，岳曉奎，張 瑩

（西北工業大學 航天學院，陜西 西安 710072）

小推力轉移軌道設計與優化問題逐步成為研究的熱點[1-2]，與傳統的火箭發動機相比，小推力發動機具有比沖高、質量輕的特點，可有效減少燃料消耗，提高任務的有效載荷，降低發射成本。但由于其推力小（通常為mN量級）、作用時間長導致小推力軌道的動力學非線性嚴重，這給小推力軌道的設計帶來了難題。小推力轉移軌道設計問題可歸結為求解有約束的連續最優控制問題。學者們針對該問題所采用的方法包括間接法和直接法[3-4]。

間接法基于變分法將最優控制問題最終轉換為一個兩點邊值問題，但這種方法收斂半徑小，對協狀態的初始猜測值很敏感，對于復雜約束難以處理。相對間接法，直接法在收斂的魯棒性和解決實際問題的適應性上具有優勢。直接法是將最優控制問題離散成參數優化問題，然后利用非線性規劃方法求解。高斯偽譜方法[5-6]是最近研究較多的直接配點優化方法，相對于其他直接配點法[7]的優勢是可以用較少的節點獲得較高的精度。麻省理工學院的Benson從理論上證明了高斯偽譜法的KKT條件與最優控制理論中的一階必要條件是一致的；并且，由于其無需猜測協狀態的初始值，這就大大降低了求解最優控制問題的難度。

文中研究了基于高斯偽譜法的燃料最省小推力轉移軌道設計問題。首先建立了星際小推力軌道優化模型，對轉移軌道參數進行了無量綱化處理以提高數值計算精度。然后利用高斯偽譜方法將轉移軌道優化問題轉化為多約束的非線性規劃問題，并應用SNOPT優化軟件包求解了最優轉移軌道的推力控制角變化規律。

1 小推力軌道優化問題

只考慮探測器在星際巡航段的轉移軌道設計問題，采用笛卡爾坐標系下的小推力探測器動力學模型：

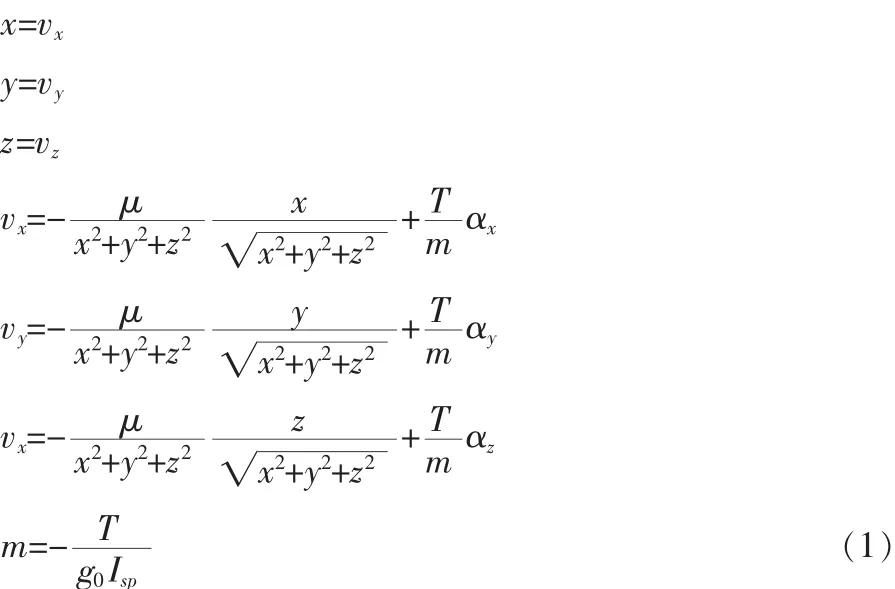
其中，r=[x，y，z]T為探測器在日心黃道慣性系中的位置矢量，v=[vx，vy，vz]T為發動機推力在各個方向上的加速度矢量，m為飛行器和推進劑的總質量； 為太陽引力系數； 為推力幅值；α=[αx，αy，αz]T為發動機推力在各個方向的加速度矢量；g0為海平面重力加速度；Isp為發動機比沖。

假定小推力發動機的輸入功率P隨著探測器日心距離的增大而減小，它與探測器日心距離的平方成反比，即

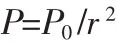
其中，P0為探測器日心距離為1AU時的輸入功率，r采用天文單位。發動機推力T為：

其中，η為推進器的工作效率。

在推進器連續工作條件下，探測器從地球發射與目標星體的燃料最省轉移軌道的性能指標可以寫成：

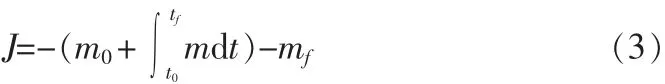
探測器的發射時間和到達時間均不固定，對于任何的發射時間t0，探測器受到地球星歷約束，探測器的位置和速度需要滿足下面的等式約束

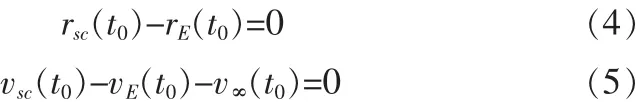
其中，rsc，vsc是發射時刻探測器在日心黃道坐標系中的位置和速度；rE，vE是地球的位置和速度；v∞是地球逃逸雙曲線超速，其大小已知，方向不確定。由公式（4），（5）構成了探測器軌道的初始邊界條件：

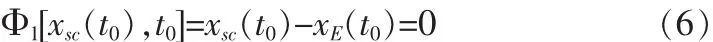
當探測器與目標星體交會時，探測器的位置和速度需要滿足下面的等式約束：

其中，tf是探測器與目標星體的交會時間；rt（tf），vt（tf）是探測器交會時目標星體的位置和速度。由公式（7）、（8）構成了探測器軌道的末端邊界條件：

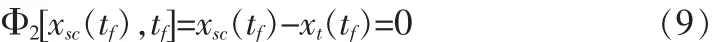
在轉移過程中，推力方向矢量必須滿足如下條件：

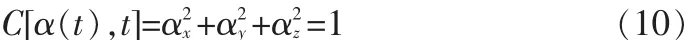
則星際探測任務的燃料最省轉移軌道可以描述為：尋求最優的發射時間t0，連續的軌道狀態 xsc（t），連續的推力方向矢量α（t）和交會時間tf，使探測器軌道在滿足動力學約束（1），邊界約束（6）和（9），推力方向矢量約束（10）的條件下，使性能指標（3）達到最小。

尋優參數可以表示為：

為提高計算精度，避免利用高斯偽譜方法求解過程中出現病態矩陣，需要對軌道參數進行無量綱化處理，使各狀態參數的取值范圍都在一個相近的數值范圍內。為此，文中取量綱質量單位[M]=m0；量綱距離單位[L]=AU；量綱時間單位[T]=。下面將采用高斯偽譜法對上述小推力軌道優化問題進行處理。

2 高斯偽譜方法

高斯偽譜法的基本求解思路為：將未知的軌道狀態和控制時間歷程在一系列高斯點上離散化，而后用這些離散的狀態與控制分別構造Lagrange插值多項式去逼近真實的軌道狀態與控制，再通過對狀態量求導來代替動力學微分方程。

由于高斯點分布在（-1，1）區間，若要把動力學方程在高斯點上進行離散，首先需要把所研究問題的時間區間t∈[t0，tf]轉換到τ∈[-1，1]，這個轉化可以通過下式完成：

高斯偽譜法取 N 個高斯點 τ1，τ2，…，τN和初始端點 τ0=-1上的離散狀態構造Lagrange插值多項式去近似狀態的時間歷程，即

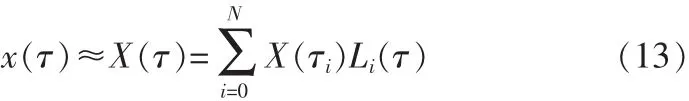
式中，x（τ）為真實的狀態時間歷程，X（τ）為由 Lagrange插值多項式近似得到的狀態時間歷程；Li（τ）為Lagrange插值基函數，i=0，1，…，N。

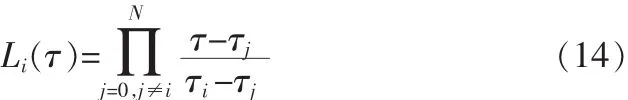
類似地，控制量的時間歷程也可以用離散的控制構造Lagrange插值多項式來近似，即

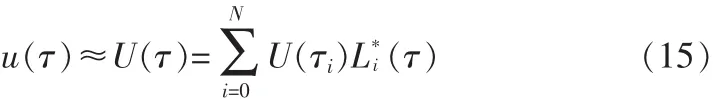
式中，u（τ）為真實的控制時間歷程，U（τ）為由 Lagrange插值多項式近似得到的控制時間歷程；（τ）為Lagrange插值基函數，i=1，…，N。

需要注意的是，構造狀態用了N個高斯點與初始端點共N+1個點，而構造控制只用了N個高斯點，因而方程（13）的腳標是從0開始，而方程（15）的腳標卻從1開始。

式（13）對時間求導，得

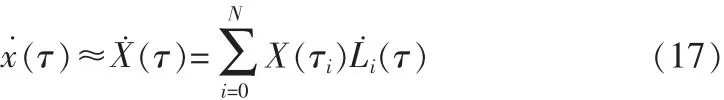
定義微分近似矩陣D，其中元素為：

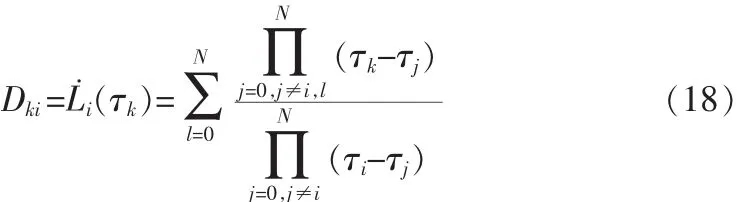
式中，D 為 N×（N+1）二維矩陣，k=1，…，N，i=0，1，…，N。

由式（17）、（18）將軌道動力學約束轉化為一系列代數約束：

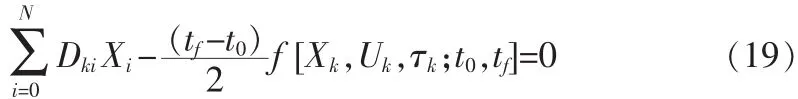
式中，Xk=X（τk），Uk=U（τk）；k=1，2，…，N， f為軌道動力學方程右端函數。

終端狀態由高斯求積公式得到：

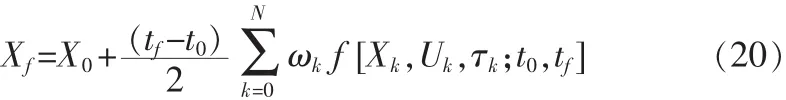
式中，X0=X（-1），ωk為高斯積分權重，有

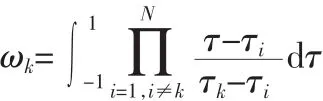
式（19）將軌道動力學約束轉化為只與節點處離散狀態和控制變量相關的代數約束，同樣，性能指標和約束條件也可以處理為只與節點處狀態和控制變量相關的形式。

如此，星際小推力軌道優化問題可以轉化為一個多約束的參數優化問題，尋優參數為發射時間、交會時間以及各節點上的狀態和控制變量：

性能指標可以表示為：

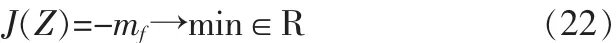
始末端邊界條件可以表示為：

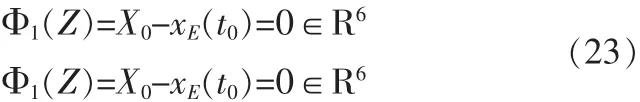
推力矢量約束可以表示為：

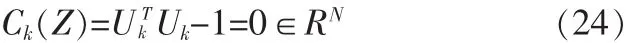
離散后的小推力軌道最優控制問題為典型的非線性規劃問題，本文采用TOMLAB/PROPT優化軟件包進行求解。

3 數值仿真與分析

為了驗證本文所提設計方法的正確性和有效性，對小推力探測器的星際轉移軌道進行設計與優化。探測器主要參數如表1所示。

表1 探測器主要參數表Tab.1 Parameters of space detector

算例一：地球-火星交會任務

采用直接打靶法和高斯偽譜法對地球-火星交會任務的燃料最省小推力轉移軌道分別進行設計。

探測任務要求探測器在2009年1月1日到2009年12月31日之間從地球出發，出發時刻認為探測器的日心位置和速度與地球相同。地球-火星交會的初始轉移時間設為365天。采用直接打靶法和高斯偽譜法優化的軌道參數如表2所示。

由表2可以看出，采用直接打靶法和高斯偽譜法的優化結果基本一致，這表明采用高斯偽譜法求解行星際小推力轉移軌道問題是有效地。采用直接打靶法求解該問題時，所用計算時間為1 712.343 8 s；采用高斯偽譜法時計算時間為56.140 6 s，這主要是由于直接打靶法在迭代過程中需要對狀態動力學方程進行積分造成的，同時也驗證了高斯偽譜法在求解小推力轉移軌道問題上的優勢。

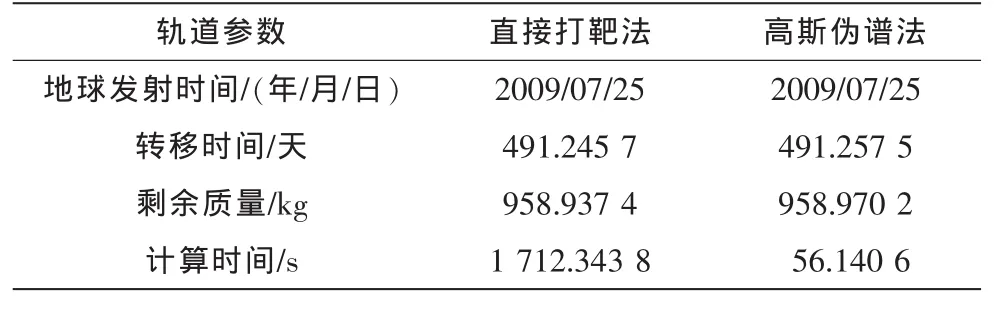
表2 地球-火星軌道優化結果對比Tab.2 Orbit optimization result of earth-mars

對于小推力軌道設計問題，通常采用俯仰和偏航兩個控制角來定義推力的指向。定義俯仰控制角α為推力矢量在軌道平面內的投影與當地水平之間的夾角；偏航控制角β為推力矢量與密切軌道平面之間的夾角，則推力的單位方向矢量就可以表示為：a=[sinαcos β cosαcos β sin β]。 直接打靶法和高斯偽譜法的控制角隨時間的變化規律如圖1所示。

由于火星軌道面與地球軌道面之間的夾角很小，偏航控制角在整個飛行過程中均較小，最大時約為20°。探測器的推力方向隨飛行軌跡的變化如圖2所示。

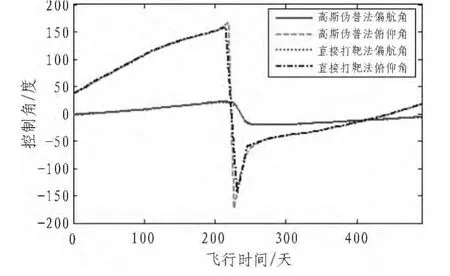
圖1 直接打靶法和高斯偽譜法控制軌線對比Fig.1 Compare of orbital control trajectory

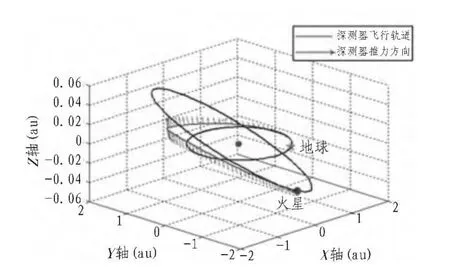
圖2 探測器飛行軌跡與推力方向Fig.2 Trajectory and thrust orientation

算例二：地球-金星交會任務

為了進一步考察高斯偽譜法求解行小推力軌道優化問題的有效性，采用高斯偽譜法對地球-金星交會任務的燃料最省小推力轉移軌道進行設計。探測任務要求探測器在2021年1月1日到2021年12月31日之間從地球出發，出發時刻認為探測器的日心位置和速度與地球相同，即探測器的地球逃逸速度為零。初始假設探測器飛行 天到達金星，此時要求探測器的日心速度等于金星的日心速度，與金星進行交會。采用高斯偽譜法優化的軌道參數如表3所示。

表3 地球-金星軌道優化結果Tab.3 Orbit optimization result of earth-mars

表2和表3中轉移時間和剩余質量的優化結果對比，說明了發動機開機時間長短對太陽能電推進器的燃料消耗的影響不大；由于發動機推力大小與探測器日心距離的平方成反比，相比于地球-火星段軌道，探測器地球-金星軌道段的推力比較大，所以剩余質量相差不大。

探測器在地球-金星交會任務中的飛行軌跡如圖3所示。

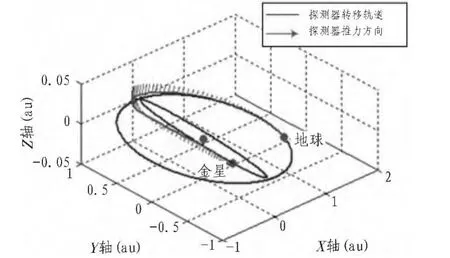
圖3 探測器飛行軌跡Fig.3 Trajectory of space detector

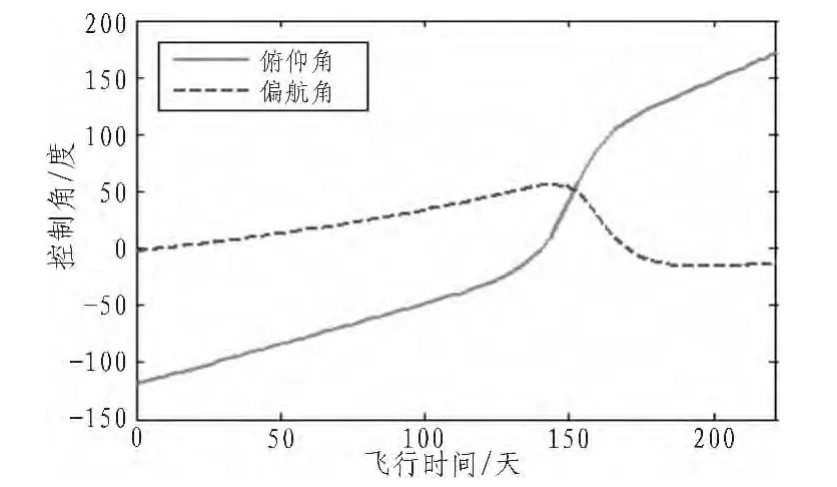
圖4 地球-金星軌道控制軌線Fig.4 Control orbital trajectory of earth-venus

從飛行軌跡圖3可以看出，在轉移軌道初始階段，發動機推力方向主要指向軌道內以減小軌道的半長軸；軌道中段，推力方向主要指向軌道面外以增加軌道傾角；在探測器接近金星的最后階段，推力方向主要指向軌道外以降低探測器的速度，避免撞擊金星。探測器在地球-金星交會任務中的發動機推力矢量控制角隨時間的變化如圖4所示。由于金星軌道面與地球軌道面之間的夾角相對較大，在整個飛行過程中，偏航控制角最大時約為。

4 結 論

文中研究了基于高斯偽譜法的小推力轉移軌道設計與優化問題。通過對燃料消耗最省火星和金星交會任務的軌道設計與分析表明：采用高斯偽譜法進行求解時，仿真初值選取相對自由，并且收斂速度快，采用此優化算法，可保證所得解最優的基礎上，有效提高問題的計算效率，具有良好的應用前景。

[1]Rayman M D，Williams S N.Design of the first interplanetary solar electric propulsion mission[J].Journal of Spacecraft and Rockets，2012，39（4）:589-595.

[2]Kugelberge J，Bodin P，Persson S，et al.Accommodating electric propulsion on SMART-1[J].Acta Astronautica，2004，55（2）:121-130.

[3]Ranieri C L，Ocampo C A.Indirect optimization of spiral trajectories[J].Journal of Guidance， Control and Dynamics，2006，29（6）:1360-1366.

[4]Betts J T，Erb S O.Optimal low thrust trajectories to the moon[J].SIAM Journal of Applied Dynamical Systems，2003，2 （2）:144-170.

[5]Benson D A.A gauss pseudospectral transcription for optimal control[D].Massachusetts:Department of Aeronautics and Astronautics， Massachusetts Institute of Technology，2005.

[6]Benson A，Thorvaldsen T，Rao V.Direct trajectory optimization and costae estimation via an orthogonal collocation method[J].Journal of Guidance， Control and Dynamics，2006，29 （6）:1435-1440.

[7]Betts J T.Very low-thrust trajectory optimization using a direct SQP method[J].Journal of Computation&Applied Mathmatics，2009，120（1）:27-40.