基于ADAMS的砂輪磨齒機加工過程的動力學分析及仿真

戚偉岸，李小寧，涂煒

（南京理工大學機械學院，江蘇南京 210094）

0 引言

齒輪作為機械傳動系統中的重要傳動部件，其制造精度的提高具有重要意義。蝸桿砂輪磨齒機作為一種高效、高精度的齒輪精加工機床，采用滾切法原理來加工，即用蝸桿式砂輪與齒輪（工件）展成嚙合的原理來磨削工件。齒輪加工中由于刀架與工件的受力而產生的刀架與工作臺的跟蹤誤差是現在數控機床普遍存在的誤差源之一，如何減小這一誤差是提高機床精度的關鍵所在。

基于ADAMS的齒輪加工動力學仿真，對齒輪加工過程中的嚙合力進行了仿真分析，為進一步分析齒輪加工過程中由于受阻力產生的跟蹤誤差奠定了理論基礎。

1 三維實體建模及數據轉換

1.1 三維實體建模

機械動力學仿真軟件ADAMS（automatic dynamic analysis of mechanical systems）是對機械系統的運動學及動力學進行仿真計算的軟件，集建模、計算和后處理于一體［1］。ADAMS雖然具有強大的運動學及動力學仿真能力，但是在三維建模方面相對于其他CAD軟件卻有所不及，特別是針對相對復雜的機械零件建模，本文采用常用的CAD軟件PRO/E建立了刀架與工作臺的實體模型，如圖1所示。

1.2 數據轉換

有兩種方法可以實現PRO/E與ADAMS之間的數據轉換。

圖1 刀架與工作臺實體模型

1）在PRO/E中建立好實體模型后，將模型定義為IGES，stereolithography，render等文件格式，在 ADAMS 中導入幾何模型。

2）利用PRO/E與ADAMS的專用接口軟件Mechanism/PRO進行轉換。在轉換過程中要注意PRO/E中建模的單位與ADAMS中定義的單位保持一致，否則會導致轉換的失敗。采用第一種方法進行數據轉換。

2 動力學模型簡化及參數設定

2.1 動力學模型簡化

由于實際刀架與工作臺是固定的，并且機床本身自帶動平衡裝置，因此在做動力學分析時可以將刀架工作臺進行簡化，但簡化模型必須遵循以下幾個原則:

1）簡化后運動副與原模型相同;

2）在不影響機構運動的情況下，簡化模型盡量簡單;

3）對于多個零件固聯時，可以將這多個零件看做一個整體。

簡化后的實體模型如圖2所示。

圖2 實體簡化模型

將模型導入ADAMS后，在ADAMS環境下對模型進行施加約束，添加運動副，施加驅動等操作進行仿真。

2.2 參數設定

磨齒的過程可以近似的看做蝸輪齒輪的嚙合過程，而齒輪在嚙合過程中嚙合力并不是保持不變的，而是每嚙合入一個齒就產生一個脈沖力［2］。因此在定義齒輪加工過程中的作用力時可以將該力定義為接觸力。在ADAMS中有兩種計算接觸力的方法，一種是補償法（restitution），另一種是沖擊函數法（impact）。補償法需要確定兩個參數:懲罰系數和補償系數。懲罰系數確定兩個構件之間的重合體積的剛度，補償系數決定兩個構件在接觸時的能量損失。沖擊函數法是根據Impact函數來計算兩個構件之間的接觸力，接觸力由兩個部分組成:一個是由于兩個件之間的相互切入而產生的彈性力;另一個是由相對速度產生的阻尼力。本文采用沖擊函數法來進行仿真。Impact函數值由自變量函數值決定其有無，

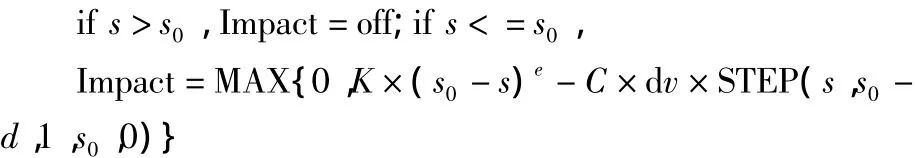
式中:s表示位移變量，dv表示速度變量，s0表示碰撞力激發的位移值，e表示碰撞指數，K表示剛度系數，C表示阻尼系數，d表示阻尼逐漸增大的位移值。

齒輪加工中所產生的脈沖力問題可以看做兩個變曲率半徑柱體撞擊問題，要解決此問題可以采用Hertz靜力彈性理論。

由文獻［3］可以得到撞擊時法向力 P和變形δ關系為:

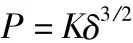
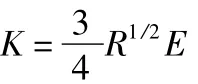
3 仿真控制與計算分析

3.1 仿真控制

仿真控制是決定仿真計算的類型、仿真時間、方程步數和仿真步長等信息，仿真控制有兩種方式，一種是交互式，另一種是腳本式。交互式是普通的方式，它可以完成多數的仿真，腳本控制不僅能完成交互式的所有功能，還能完成一些特殊功能。本文采用腳本式控制仿真中的simpe run控制，其動畫仿真如圖3。

圖3 動畫仿真圖

3.2 仿真分析

磨齒機的一般工作轉速是4000 r/min和5 000 r/min，這里對這2種轉速下對齒輪加工嚙合力在時域和頻域下進行分析。設置仿真時間t=0.5 s，STEP=800。在 4000 r/min時，受力與轉矩圖如圖4，在5 000 r/min時，受力與轉矩圖如圖5。

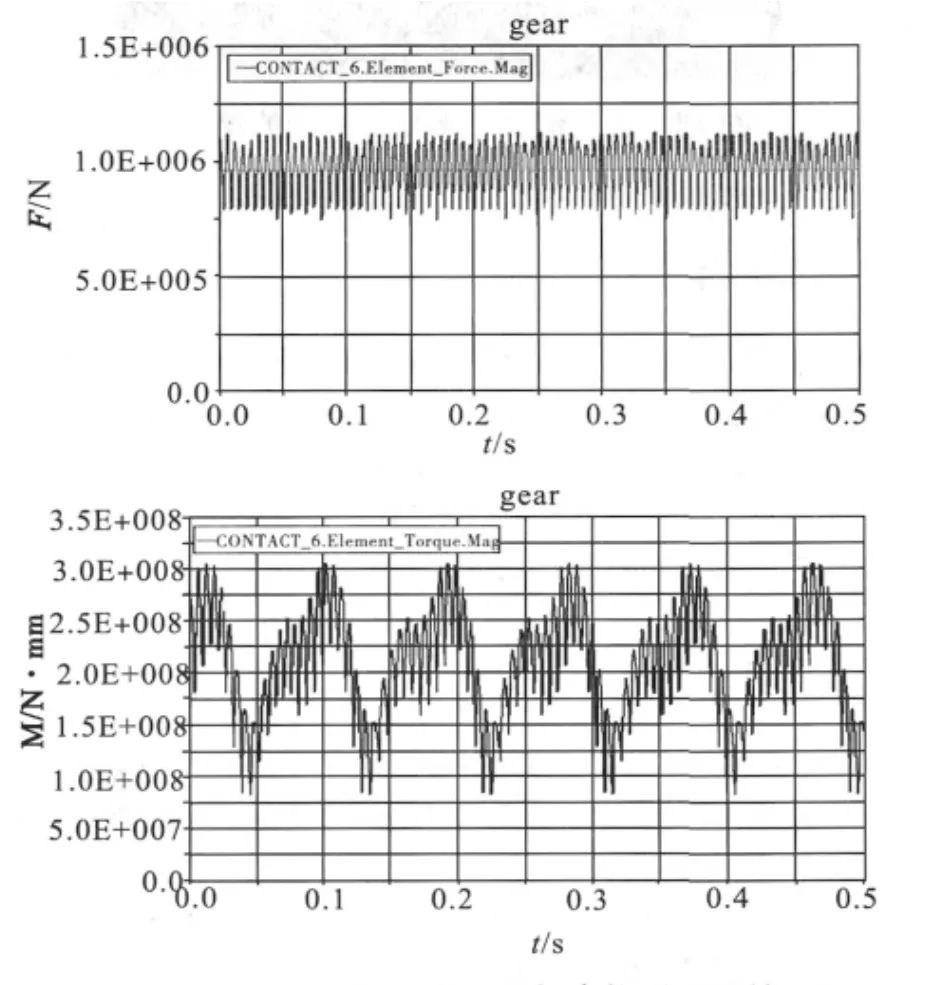
圖4 4 000 r/min時加工中刀具與齒輪受力及轉矩圖

圖5 5 000 r/min時加工中刀具與齒輪受力及轉矩圖

4 結論

由以上仿真分析可以看出:磨齒機在加工過程中由于刀具與齒輪間的作用力以及產生的轉矩都在某一值周圍上下波動且呈現周期性，并且已經成為了影響刀架、工作臺電動機轉動的不可忽略的因素。從圖4和圖5中可以看出，在4 000 r/min時受力及轉矩相對于5 000 r/min時較為平緩，特別是轉矩在5 000 r/min時有較大的波動。這與磨齒機在這兩種轉速下加工精度受到影響的實際情況是相符合的。證明了以上建立的數學模型及參數選擇是正確的，為今后解決減小跟蹤誤差建立了理論依據。

［1］李增剛.ADAMS入門詳解與實例［M］.

［2］李金玉，勾志踐，李媛.基于ADAMS的齒輪嚙合過程中齒輪力的動態仿真［J］.設計與研究，2005（1）:15-17.

［3］龍凱，程穎.齒輪嚙合力仿真計算的參數選取研究［J］.計算機仿真，2002（6）.

［4］王裕國，潘峰，胡靜倩.多種動態模擬和復雜三維動畫控制的框架結構［J］.軟件學報，1997，8（8）:615-621.