絞吸挖泥船水流作用力數值模擬

張盼盼，徐立群，倪福生

（河海大學疏浚技術教育部工程研究中心，江蘇常州 213022）

絞吸挖泥船是目前世界上在疏浚工程中使用較廣泛的一種挖泥船，其左右橫移是挖掘水下土壤的主要工藝過程。在橫移過程中，船舶受到的阻礙，主要來自于絞刀切削土壤的阻力，此外，水流對船體的作用力也不容忽視。挖泥船施工作業時，變化的水流作用力會影響船舶的操控甚至有可能危及船舶的安全［1］。所以，研究水流對船體作用力特性至關重要［2］。關于系泊船舶受水流作用力的影響，目前已有不少成果［3-4］，針對絞吸挖泥船近海作業時受水流作用力的影響進行了詳盡計算分析。利用Fluent軟件，采用雷諾N－S方程和RNGk－ 湍流模型，對船體在不同來流角度及速度下水流作用的流場進行數值模擬，得到了各情況下水流對船體的阻力及阻力系數，可供絞吸挖泥船設計及施工時參考。

1 數值計算模型

1.1 控制方程和湍流模型

本文將流體視為不可壓縮流體，流動為定常流動，其控制方程為三維連續性方程和三維不可壓縮的N－S方程。方程描述如下。

連續性方程:

動量方程:

目前，使用廣泛的湍流模型有標準k－ 兩方程模型和重整化群RNGk－ 模型，兩者的k方程和 方程是相同的，不同的是后者采用的系數不是根據試驗而是由理論推導所得。相比較標準k－ 模型，RNGk－ 模型應用更為廣泛。（關鍵是哪個模型更適合，精度更高?）

1.2 計算模型與網格劃分

a）計算模型

圖1 絞吸式挖泥船

絞吸式挖泥船如圖1所示，［5］利用定位樁和左、右錨三點定位，通過收放兩側橫移鋼纜，使挖泥船圍繞定位樁左右橫移，實現對水下巖土的連續切削，被絞刀切削的土方與水混合后由泥泵和管道輸送至指定地點。絞吸式挖泥船施工時圍繞定位樁橫移，運動速度很慢，故船體結構都是設計成箱式的，而非通常船舶的流線型結構。本文探討的水流阻力問題，可視為靜止船舶的繞流問題。絞吸式挖泥船受水流作用力的部分主要有箱型船體、絞刀架及定位樁，且船體是主要部分，本文先對船體水流作用力進行重點分析，再考慮絞刀橋架及定位樁的影響。

以某大型絞吸船為例進行分析計算，該船型長L=86.1 m，型寬W=18.2 m，型高H=5.2 m，吃水 3.5 m。坐標系選取來流方向為x軸，垂直于水面的方向為y軸，水平面中垂直于來流的方向為z軸，定義船體縱截面與來流方向的角度為θ。如圖2所示。

圖2 船體模型及受力示意圖

b）網格劃分

計算區域網格采用分塊劃分，建立兩個長方體流體區域，其中大區域尺寸約為船體區域尺寸的5倍。取不同角度時，流體大、小區域尺寸隨 的不同作相應改變。θ為0時船體所在的長方體流體小區域長200 m，寬100 m，高15 m，船體所在的長方體流體大區域長500 m，寬300 m，高30 m。船體所在的長方體流體小區域對本文研究影響較大，且形狀相對比較復雜，故此部分網格劃分應相對較密，采用混合網格。流體大區域周邊區域影響較小，且形狀簡單，故此部分網格劃分相對較稀疏，采用正六面體網格。整個區域網格總數為60110萬不等。

1.3 邊界條件

選取4種邊界面，即流入（in－let）、流出（out－let）、外邊界（boundary）、和船體（ship），相應各邊界的邊界條件為速度流入（velocity－inlet）、自由出口（outflow）、對稱邊界（symmetry）和壁面（wall）。

入口 in－let，設為速度入口;出口out－let，設為自由出口，這是因為對于出流未知的情況，通常采用自由出口，若采用壓力出口，還需確定其壓力分布，很不方便。下邊界、前邊界及后邊界的物理外形及流動結果均呈現鏡像對稱特征，故設為對稱邊界。上邊界設為對稱邊界實屬無奈之舉，此邊界若設為壓力邊界更符合實際情況，但此邊界的流出與回流難以控制，這常常使計算過程中的連續項不收斂，設置成對稱邊界相當于此邊界的內外無質量和動量的交換，利于計算的收斂［6］;ship為船體，故設為壁面邊界。

2 計算模型的驗證

為了驗證本文采用模型的可行性，采用相同設置對圓柱繞流進行模擬計算。圓柱體直徑1 m，網格劃分如圖3所示，邊界條件為速度入口、自由出口，其余邊界為壁面，取不同雷諾數計算得到阻力系數，查閱文獻［7］圓柱體的阻力系數與雷諾數的關系曲線圖得到圓柱體阻力系數的參考值，對比與圖4的結果如表1所示。

表1 不同雷諾數下圓柱體阻力系數計算結果

由表1可知，計算阻力系數與專業教科書上查到的阻力系數很接近，故本文關于湍流模型的相關設置及網格劃分、邊界條件的設置等是可行的。

3 計算結果與分析

3.1來流角度的影響

絞吸船工作時，利用裝在船體上的鋼樁和鋼樁的起落裝置來實現船體的定位和前后移動，纜繩通過絞刀橋架與固定在船體兩側的橫移錨連接，船體通過收放兩側纜繩來實現自身的左右橫移擺動。當船體左右橫移擺動時，便出現了角，角的大小直接影響到船體所受到的來流阻力的大小。定義x方向的阻力為Fx，z方向阻力為Fz。當 角取不同值時，船體的迎流面積A會發生變化。為便于計算，本文定義船體的橫截面迎流面積為A1，縱截面迎流面積為A2，船體縱向阻力為F1，船體側向阻力為F2，如圖2所示。將Fluent計算得到的Fx，Fz分解為F1，F2表示，則F1，F2可按下式求取:

相應的阻力系數按下式求取:

式中:Cd1——船體縱向阻力系數;

Cd2——船體側向阻力系數;

ρ——來流密度，本文來流為水流，取 =1 000 kg/m3;

V∞——來流速度，取V∞=1 m/s;

A1=18.2 ×3.5=63.7 m2;

A2=86.1 ×3.5=301.35 m2。

來流速度以V∞ =1 m/s為例，各來流角度下，阻力F1，F2及阻力系數Cd1，Cd2如圖 5、圖 6 所示。

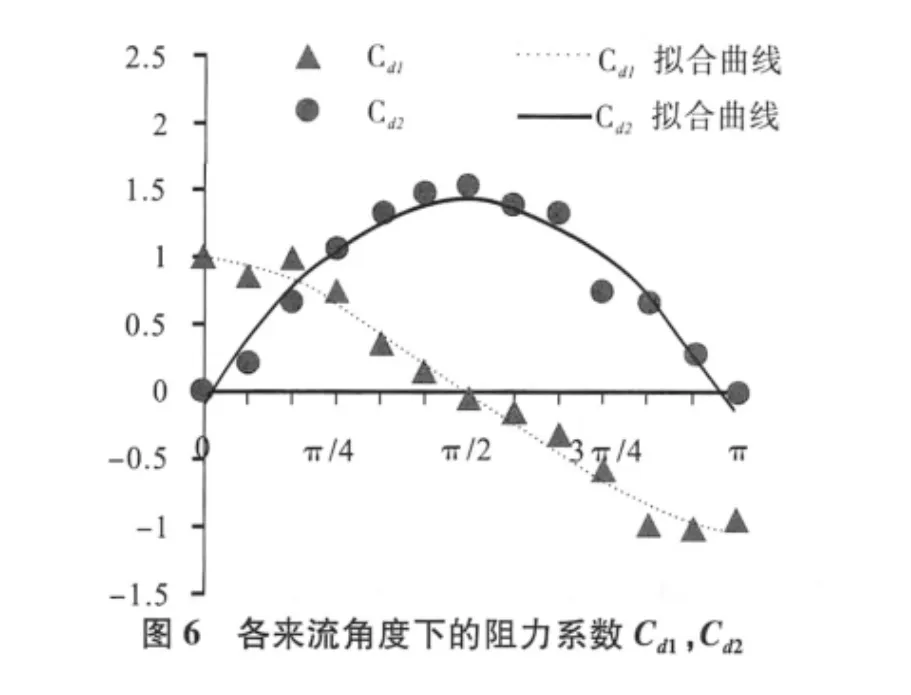
由圖5、圖6可知:1）船體受到的阻力及阻力系數大小關于θ=π/2呈基本對稱趨勢，對稱角度的阻力值、阻力系數值大小基本相等，這是因為船體左右對稱，艏艉結構近似的緣故;2）從數量上看，側向阻力F2遠大于縱向阻力F1;3）船體縱向阻力F1及其阻力系數Cd1在θ=0和θ=π時最大，θ=π/2時為零;船體側向阻力F2及其阻力系數Cd2在θ=π/2時最大，θ=0和θ=π時為零。

阻力系數擬合公式為:

船體在部分角度的速度流線圖如圖7所示:

圖7 船體部分角度的速度流線圖

由圖7可知:1）來流角度改變，船體周邊流場的流動狀態發生顯著變化;2）由于船體對水流的阻擋作用，流動發生分離，船體背流區出現渦流，導致阻力增大，隨著水流由縱向變為側向（θ由0變為π/2），渦流區域增大，阻力隨之增大，在θ=π/2時阻力達到最大。

3.2 來流速度的影響

分別以縱向阻力最大和側向阻力最大所對應的來流角度θ=0和θ=π/2為例，來研究來流速度對船舶阻力及阻力系數的影響。來流速度分別取0.25 m/s，0.5 m/s，0.75 m/s，1 m/s，1.25 m/s，1.5 m/s。

a）阻力

θ=0時，不同來流速度下船體縱向阻力F1計算結果如圖8所示，由于對稱性，船體側向阻力F2≈0;θ=π/2時不同來流速度下船體側向阻力F2計算結果如圖9所示，由于對稱性，船體縱向阻力F1≈0:

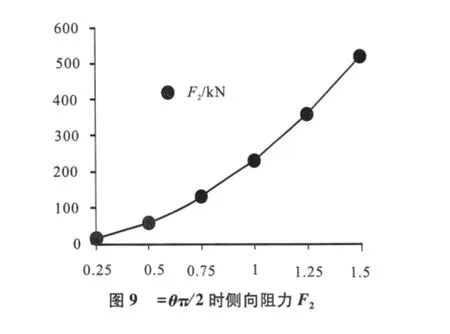
由圖8、圖9可以看出，θ=0時船體縱向阻力F1和θ=π/2船體側向阻力F2均隨速度的增大而增大。

船體阻力擬合公式如下:

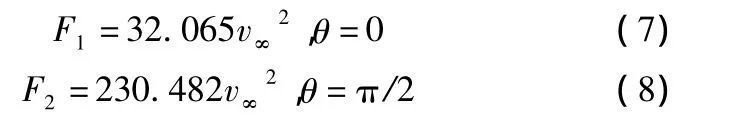
由式（7）、（8）可知，船體受到的阻力與來流速度的平方成正比。

b）阻力系數

θ=0時不同來流速度下船體縱向阻力系數Cd1和θ=π/2時不同來流速度下船體側向阻力系數Cd2的計算結果如表2所示。

表2 θ=0縱向阻力系數Cd1和θ=π/2側向阻力系數Cd2

由表2可知，θ=0時船體縱向阻力系數Cd1和θ=π/2時船體側向阻力系數Cd2均與速度的大小無關，Cd1為1.01，Cd2為 1.53。

3.3 絞刀架與樁的影響

除了船體，絞刀架及定位樁對水流作用力也有貢獻，針對縱向阻力最大和側向阻力最大兩個典型工況，對包含絞刀架及定位樁在內的整個船舶的作用力進行了計算分析，計算結果如表3所示。

表3 θ=0縱向阻力系數Cd1和θ=π/2側向阻力系數Cd2

由表3可知，絞刀架與定位樁對水流阻力的影響較大，對阻力系數的影響較小。

4 結論

本文通過使用Fluent軟件，采用RNGk－ 湍流模型，分別對船體在不同角度、不同流速時的周邊流場進行了數值模擬，得到了不同來流角度、來流速度下船體周邊流動狀態的變化及船體阻力、阻力系數的變化規律，對絞吸挖泥船設計及施工具有指導意義，主要結論如下:

1）船舶阻力與來流角度及來流速度有關，同一來流角度下，船舶阻力與來流速度平方成正比;而阻力系數只與來流角度有關，與來流速度無關，對于本文船型，阻力系數計算公式見式（5）、（6）。

2）船體縱向阻力系數Cd1的變化范圍為0～1，θ=0時最大，為1.01;船體側向阻力系數Cd2的變化范圍為0～1.5，θ=π/2 時最大，為1.53。

3）船體側向阻力F2遠大于縱向阻力F1。對于型長86.1 m、型寬 18.2 m、型高 5.2 m、吃水 3.5 m、產量為3 500 m3/h的船舶而言，當V∞=1 m/s（流速2節）、θ=π/2（側向）時，船體受到的水流阻力約為230.77 kN，約為此類絞吸船橫移鋼纜最大拉力的50%;當V∞=1 m/s（流速2節）、θ=0（縱向）時，船體受到的水流阻力約為32.08 kN。所以，船舶現場布置時，應盡量避免出現側面來流的情況，以減小水流的阻力，這樣既有利于充分利用橫移鋼纜拉力切削土壤，又有利于船舶的操控，提高施工安全性。

［1］劉明俊，齊傳新.風、流對航行安全影響的探討［J］.水運科技信息，1998（3）:32-34.

［2］李水泉.黃河水上船舶阻力分析與計算［J］.甘肅科技，2011，27（12）.

［3］張福然，趙軍，張學勤.水流對離岸海港碼頭系泊船舶作用力的研究［J］.水道港口，1995（1）:1-11.

［4］張福然，趙軍.水流對順岸碼頭上系泊船舶作用力的研究［J］.水運工程，1995（3）:52-55.

［5］倪福生.國內外疏浚設備發展綜述［J］.河海大學常州校區學報，2004（1）.

［6］韓占忠.FLUENT流體工程仿真計算實例與分析［M］.北京:北京理工大學出版社，2009.

［7］孔瓏.工程流體力學［M］3版.北京:中國電力出版社，2006.