基于四元數自補償四旋翼飛行器姿態解算
馬 敏,吳海超
MA Min,WU Hai-chao
(中國民航大學 航空自動化學院,天津 300300)
0 引言
四旋翼(Quad-Rotor)無人飛行器是由四螺旋槳驅動的、能夠實現垂直起降的飛行器,由前后和左右兩組旋翼組成,旋轉時對應方向上電機旋轉方向相反,其與一般直升機最主要的不同點是四旋翼飛行器不需要用尾槳來平衡機體。特別適合在近地面環境中執行監視和偵察等任務,具有廣闊的軍事和民用前景[1]。
其中,姿態解算的精度是實現飛行器穩定飛行的前提。而體積小、功耗低及易于集成的MEMS 傳感器是實現低成本航姿測量的最佳選擇,主要由三軸陀螺儀、三軸加速度計和三軸電子羅盤組成。MEMS 陀螺儀測量精度較低,雖然動態性能良好,但存在累計漂移誤差,加速度計和電子羅盤有著較好的靜態特性,沒有漂移問題,但容易受機體振動和外部磁場等因素的干擾,使其動態可信度降低[2];為有效抑制慣性器件常值偏差對慣導系統的影響,本文設計了四元數自補償方法。由于旋轉的引入,慣導系統中陀螺儀和加速度計的常值偏差被調制成正弦信號,通過積分運算可以有效地消除常值偏差對慣系統的影響。實現了長時間穩定地輸出準確姿態數據。
1 導航坐標系描述
所謂姿態解算是指將運載體上慣性單元的輸出,實時轉換成運載體的姿態。這里的姿態通常指機體坐標系(b系)相對于導航坐標系(n系)的角位置。
導航坐標系(n系),它的原點位于載體質心,x、y和z 軸的方向選為東北天(ENU)右手坐標系。機體坐標系(b系)的原點與載體質心重合,對于飛行器而言,x 軸沿載體橫軸向右,y軸沿載體縱軸向前,z 軸沿載體豎軸向上,即“右前上”坐標系,可見,機體坐標系是與載體固連的[3]。根據機體坐標系和地理坐標系之間的相對角位置關系,可以定義載體的 3 個姿態角,分別為偏航角j、俯仰角q和橫滾角g,如圖1所示。
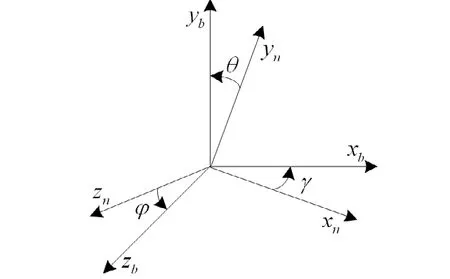
圖1 機體坐標系和導航坐標系角度關系
機體系(b)和導航系(n)之間的方向余弦陣可由式(1)表示:

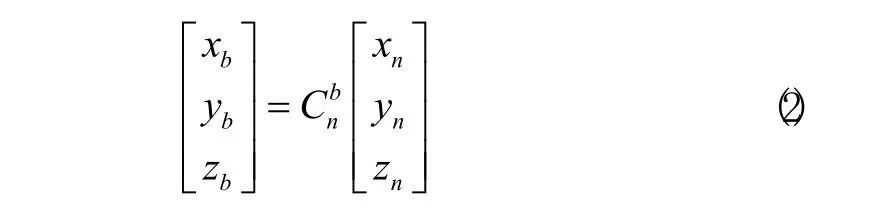
2 四元數自補償算法研究
2.1 姿態解算的四元數法
四元數,是由一個實數和三個虛數組成的“超復數”,表示為:
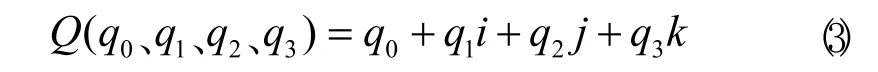
在計算運載體姿態時,當只關心機體坐標系相對于導航坐標系的角位置時,可以認為機體坐標系(b系)是由導航坐標系(n系)經過一次性等效旋轉形成的,四元素Q包含了這種等效旋轉的全部信息[4]。其姿態變換公式如式(4)所示:

剛體轉動理論中,依歐拉定理,式(1)的四元數表示為:
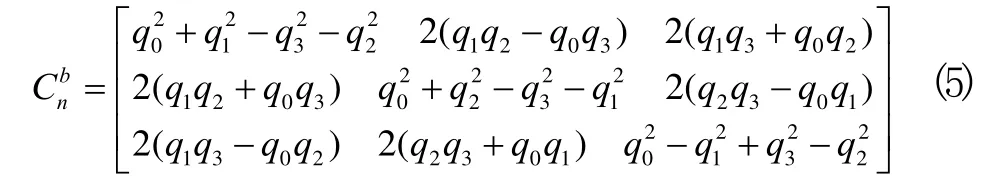
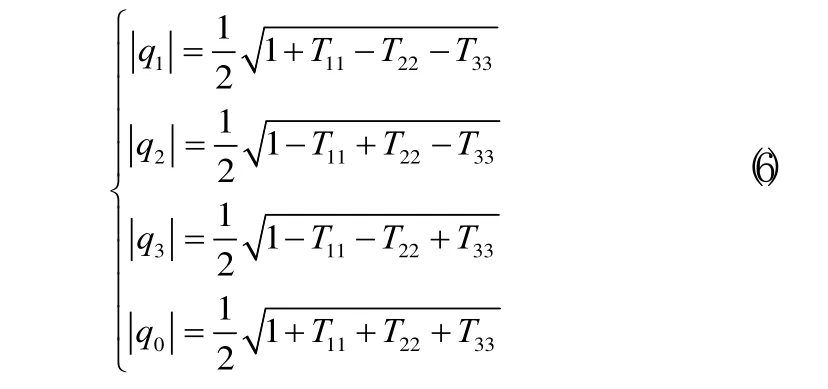

由旋轉矩陣式(1)得到的歐拉角求解公式如下:
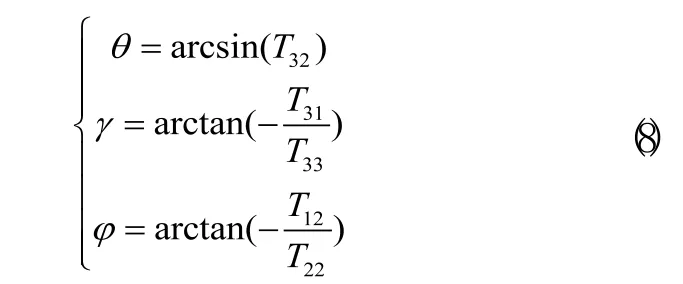
偏航角j、橫滾角g真值通過表1和表2確定。
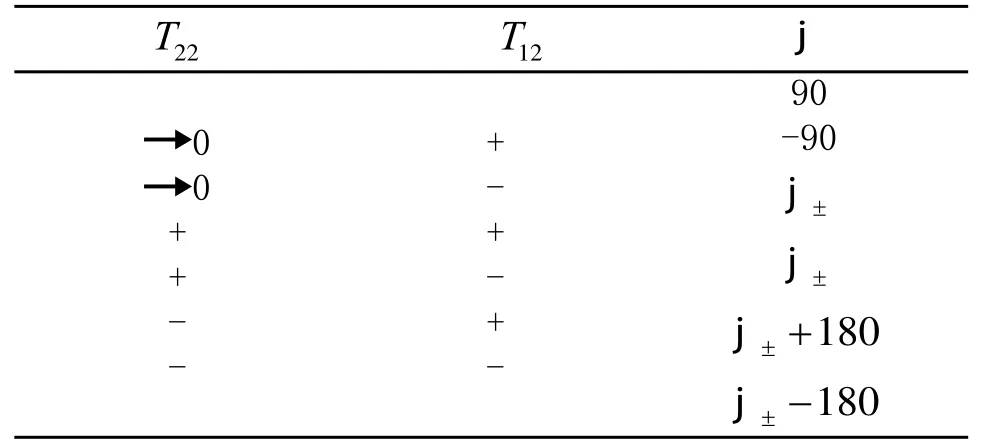
表1 偏航角真值表
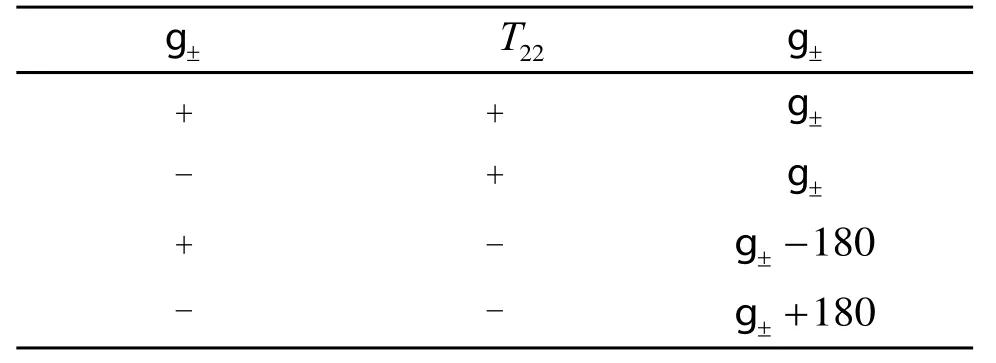
表2 翻滾角真值表
由于四旋翼飛行器飛行高度低,飛行速度慢,可以忽略地球自轉等因素的影響,那么四元數Q具有如下微分方程關系:
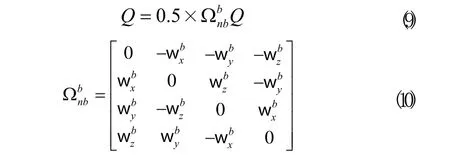
設T為采樣周期,那么四元數微分方程的一階龍格-庫塔法計算式為:

每個采樣周期讀取陀螺儀、加速度計和電子羅盤的數據,對上式進行迭代運算,即可實現四元數隨時間的更新,進而求得3個姿態角。而在實際中常值偏差是變化的,即在一次啟動后隨著陀螺儀、加速度計和電子羅盤運轉的時間的增長,慣性測量器件的常值偏差也緩慢的變化到導航系統精度無法允許的程度。
2.2 四元數自補償算法研究
在傳統的慣性導航系統中,慣性測量元件與運載體固連,它們之間沒有相對運動。四元數自動補償方法是將安裝有陀螺儀、加速度計和電子羅盤的慣導系統相對機體坐標系旋轉,使慣性器件常值偏差沿著機體系敏感軸方向呈周期性變化。可有效抑制零位誤差對系統的影響。
由于自補償算法在三個軸方向具有相同的應用,本文僅講解單軸旋轉的自補償。
設初始時刻導航坐標系(n系)與機體坐標系重合(b系),然后機體坐標系以角速度w繞ozb軸旋轉。機體坐標系和導航坐標系的夾角為wt,兩個坐標系之間的關系用方向余弦表示為[6]:
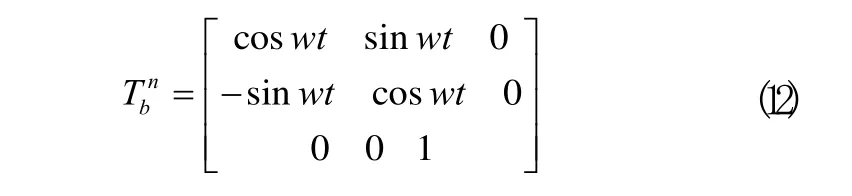
陀螺儀和加速度計的輸出從導航坐標系到機體坐標系的轉換關系表示為:

導航坐標系中陀螺儀和加速度計的輸出為:
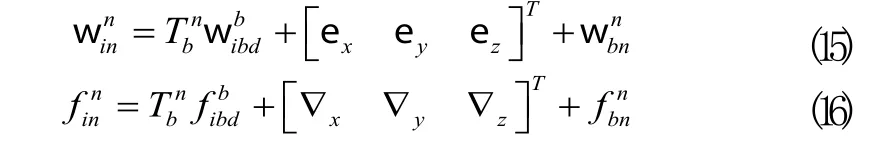
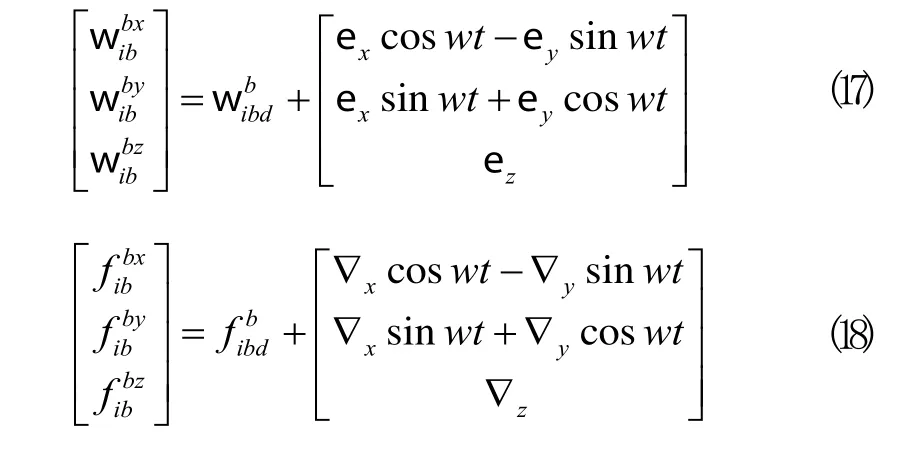
式(17)、(18)可以看出當機體坐標系以角速度w繞ozb軸旋轉時,常值陀螺漂移ex、ey和常值加速度計零位誤差?x、?y在導航坐標系oxb和oxb軸上的分量呈周期變化[7]。所以,ozb軸方向上的陀螺常值漂移和加速度計零位誤差沒有得到調制,有效抑制了慣性器件的偏差對解算精度的影響。
3 實驗結果
實驗中使用陀螺儀 L3G4200D,加速度計ADXL345和電子羅盤 HMC5883L 構成姿態解算單元,采用 TMS320F28335做為主控制器,通過I2C接口讀取3個傳感器數據進行實時姿態解算,得到的姿態角通過 SCI 接口與上位機進行通訊[8]。實驗平臺如圖2所示。

圖2 搭建硬件平臺
上位機將相應的數據繪制成曲線顯示出來。未加入補償算法得出曲線如圖 3 所示。可以看出一些時間段內翻滾角度超出了基準范圍[-90~90],所以,直接運用四元數法進行姿態解算,動態性能良好,但存在一定的漂移。圖4給出了加入自補償算法后曲線圖,其解算姿態角,既能保持在姿態角基準范圍內,又具有四元數法的良好動態特性。
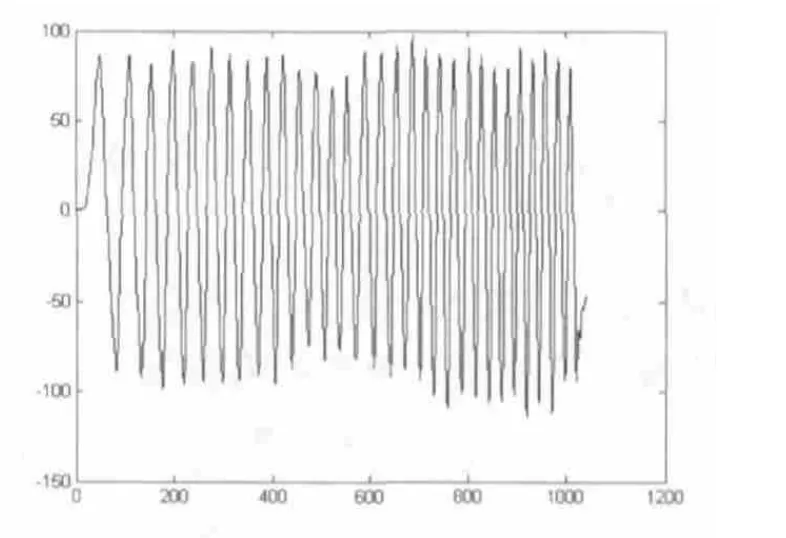
圖3 未加入自補償曲線圖
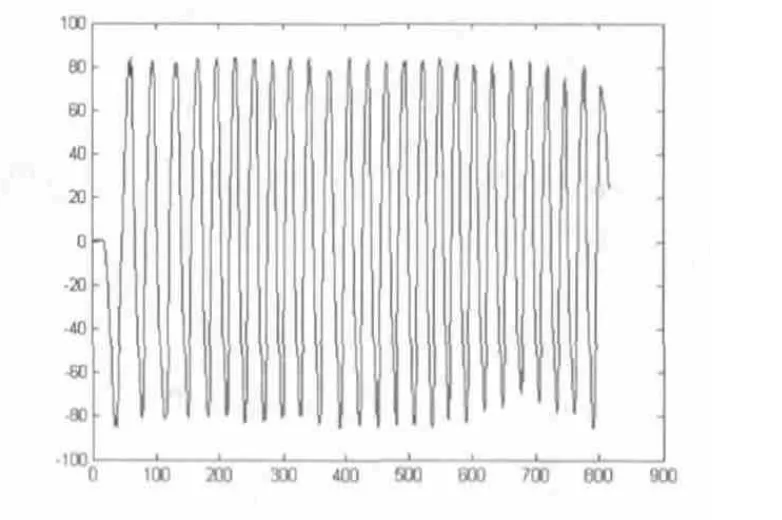
圖4 加入自補償曲線圖
4 結束語
本文分析了MEMS器件常值偏差的變化對姿態解算的影響[9],針對MEMS器件精度低、易發散的問題提出四元數自補償算法,并在小型四旋翼飛行器姿態解算系統中進行了實驗。實驗結果表明:該算法能有效抑制常值誤差的變動對姿態解算精度的影響,且保證了四元數法的良好動態特性。
[1] 單海燕.四旋翼無人直升機飛行控制技術研究[D].南京航空航天大學.2008.
[2] 聶博文,馬宏緒,王劍,等.微小型四旋翼飛行器的研究現狀與關鍵技術[J].電光與控制,2007,14(6)∶113-117.
[3] 劉俊,石云波,李杰.微慣性技術[M].北京∶電子工業出版社,2005.
[4] YANG Y,MIAO L J,SHEN J.Method of improving the navigation accuracy of SINS by continuous rotation[J].Journa1 of Beijing Institute ofTechno1ogy,2005,14(1)∶45-49.
[5] HUANG W Q,ZHAO G L,TAN ZH F,et a1.Research of Gyro case rotating monitor technique[J].Ship Bui1ding of China,2002,43∶54-59.
[6] 于旭東,王宇,張鵬飛,等.單軸旋轉對慣導系統誤差特性的影響[J].慣性技術學報,2008,16(6)∶643-648.
[7] 王其,徐曉蘇.旋轉IMU在光纖捷聯航姿系統中的應用[J].中國慣性技術學報,2007,15(3)∶265-368.
[8] 蘇奎峰,呂強,鄧志東,湯霞青.TMS320x28xxx原理與開發[M].北京∶電子工業出版社.2009.
[9] 洪森濤,金智慧,李志強.四旋翼飛行器建模及姿態穩定性分析[J].航空制造技術.2006(5).91-94.

